
Question Number 47735 by behi83417@gmail.com last updated on 14/Nov/18
Commented by mr W last updated on 14/Nov/18

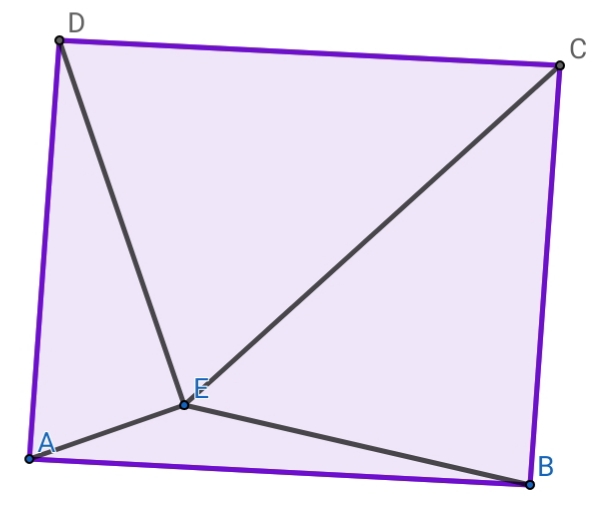
$${we}\:{only}\:{need}\:{to}\:{know}\:{the}\:{distances}\:{to} \\ $$$${three}\:{vertexes}.\:{the}\:{distance}\:{to}\:{the} \\ $$$${fourth}\:{vertex}\:{is}\:{not}\:{independent}. \\ $$
Commented by behi83417@gmail.com last updated on 14/Nov/18
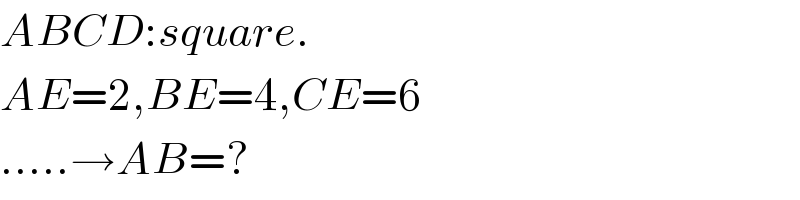
$${ABCD}:{square}. \\ $$$${AE}=\mathrm{2},{BE}=\mathrm{4},{CE}=\mathrm{6} \\ $$$$.....\rightarrow{AB}=? \\ $$
Commented by MJS last updated on 14/Nov/18
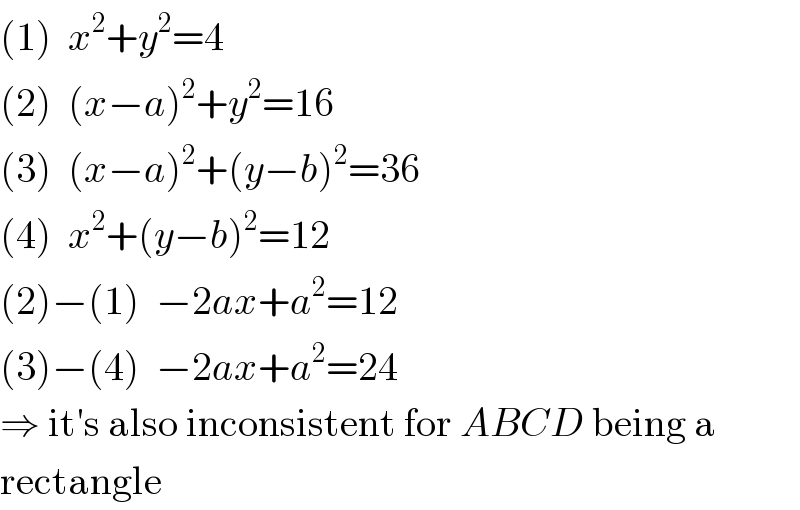
$$\left(\mathrm{1}\right)\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\:\:\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16} \\ $$$$\left(\mathrm{3}\right)\:\:\left({x}−{a}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} =\mathrm{36} \\ $$$$\left(\mathrm{4}\right)\:\:{x}^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} =\mathrm{12} \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\:\:−\mathrm{2}{ax}+{a}^{\mathrm{2}} =\mathrm{12} \\ $$$$\left(\mathrm{3}\right)−\left(\mathrm{4}\right)\:\:−\mathrm{2}{ax}+{a}^{\mathrm{2}} =\mathrm{24} \\ $$$$\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{also}\:\mathrm{inconsistent}\:\mathrm{for}\:{ABCD}\:\mathrm{being}\:\mathrm{a} \\ $$$$\mathrm{rectangle} \\ $$
Commented by MJS last updated on 14/Nov/18
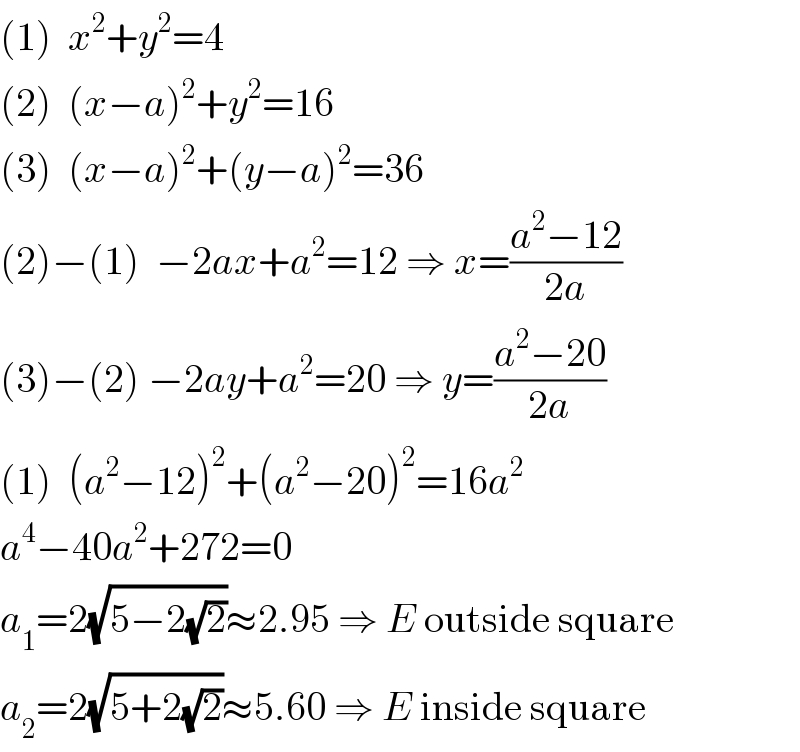
$$\left(\mathrm{1}\right)\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\:\:\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16} \\ $$$$\left(\mathrm{3}\right)\:\:\left({x}−{a}\right)^{\mathrm{2}} +\left({y}−{a}\right)^{\mathrm{2}} =\mathrm{36} \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\:\:−\mathrm{2}{ax}+{a}^{\mathrm{2}} =\mathrm{12}\:\Rightarrow\:{x}=\frac{{a}^{\mathrm{2}} −\mathrm{12}}{\mathrm{2}{a}} \\ $$$$\left(\mathrm{3}\right)−\left(\mathrm{2}\right)\:−\mathrm{2}{ay}+{a}^{\mathrm{2}} =\mathrm{20}\:\Rightarrow\:{y}=\frac{{a}^{\mathrm{2}} −\mathrm{20}}{\mathrm{2}{a}} \\ $$$$\left(\mathrm{1}\right)\:\:\left({a}^{\mathrm{2}} −\mathrm{12}\right)^{\mathrm{2}} +\left({a}^{\mathrm{2}} −\mathrm{20}\right)^{\mathrm{2}} =\mathrm{16}{a}^{\mathrm{2}} \\ $$$${a}^{\mathrm{4}} −\mathrm{40}{a}^{\mathrm{2}} +\mathrm{272}=\mathrm{0} \\ $$$${a}_{\mathrm{1}} =\mathrm{2}\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}\approx\mathrm{2}.\mathrm{95}\:\Rightarrow\:{E}\:\mathrm{outside}\:\mathrm{square} \\ $$$${a}_{\mathrm{2}} =\mathrm{2}\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}}\approx\mathrm{5}.\mathrm{60}\:\Rightarrow\:{E}\:\mathrm{inside}\:\mathrm{square} \\ $$
Commented by behi83417@gmail.com last updated on 14/Nov/18
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{MJS}.{perfect}. \\ $$
Answered by mr W last updated on 14/Nov/18
![a=distance to vertex A=2 b=distance to vertex B=4 c=distance to vertex C=6 l=side length of square x,y=distance to side BC and AB x^2 +y^2 =b^2 a^2 =(l−x)^2 +y^2 =l^2 −2lx+x^2 +y^2 =l^2 +b^2 −2lx ⇒x=((l^2 +b^2 −a^2 )/(2l)) c^2 =x^2 +(l−y)^2 =x^2 +y^2 +l^2 −2ly=l^2 +b^2 −2ly ⇒y=((l^2 +b^2 −c^2 )/(2l)) (((l^2 +b^2 −a^2 )/(2l)))^2 +(((l^2 +b^2 −c^2 )/(2l)))^2 =b^2 2l^4 +2(2b^2 −a^2 −c^2 )l^2 +[2b^4 +a^4 +c^4 −2(a^2 +c^2 )b^2 ]=4b^2 l^2 2l^4 −2(a^2 +c^2 )l^2 +[2b^4 +a^4 +c^4 −2(a^2 +c^2 )b^2 ]=0 l^2 =(((a^2 +c^2 )±(√((a^4 +c^4 +2a^2 c^2 )−2[2b^4 +a^4 +c^4 −2(a^2 +c^2 )b^2 ])))/2) l^2 =((a^2 +c^2 ±(√([(a+c)^2 −2b^2 ][2b^2 −(a−c)^2 ])))/2) l^2 =((a^2 +c^2 ±(√((a+(√2)b+c)(−a+(√2)b+c)(a−(√2)b+c)(a+(√2)b−c))))/2) l^2 =((2^2 +6^2 ±(√((64−2×16)(2×16−16))))/2) l^2 =20±8(√2) ⇒l=2(√(5±2(√2)))=5.59 or 2.95](Q47760.png)
$${a}={distance}\:{to}\:{vertex}\:{A}=\mathrm{2} \\ $$$${b}={distance}\:{to}\:{vertex}\:{B}=\mathrm{4} \\ $$$${c}={distance}\:{to}\:{vertex}\:{C}=\mathrm{6} \\ $$$${l}={side}\:{length}\:{of}\:{square} \\ $$$${x},{y}={distance}\:{to}\:{side}\:{BC}\:{and}\:{AB} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} =\left({l}−{x}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={l}^{\mathrm{2}} −\mathrm{2}{lx}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={l}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{lx} \\ $$$$\Rightarrow{x}=\frac{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{l}} \\ $$$${c}^{\mathrm{2}} ={x}^{\mathrm{2}} +\left({l}−{y}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{l}^{\mathrm{2}} −\mathrm{2}{ly}={l}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ly} \\ $$$$\Rightarrow{y}=\frac{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{l}} \\ $$$$\left(\frac{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{l}}\right)^{\mathrm{2}} +\left(\frac{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{l}}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\mathrm{2}{l}^{\mathrm{4}} +\mathrm{2}\left(\mathrm{2}{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −{c}^{\mathrm{2}} \right){l}^{\mathrm{2}} +\left[\mathrm{2}{b}^{\mathrm{4}} +{a}^{\mathrm{4}} +{c}^{\mathrm{4}} −\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){b}^{\mathrm{2}} \right]=\mathrm{4}{b}^{\mathrm{2}} {l}^{\mathrm{2}} \\ $$$$\mathrm{2}{l}^{\mathrm{4}} −\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){l}^{\mathrm{2}} +\left[\mathrm{2}{b}^{\mathrm{4}} +{a}^{\mathrm{4}} +{c}^{\mathrm{4}} −\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){b}^{\mathrm{2}} \right]=\mathrm{0} \\ $$$${l}^{\mathrm{2}} =\frac{\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\pm\sqrt{\left({a}^{\mathrm{4}} +{c}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} {c}^{\mathrm{2}} \right)−\mathrm{2}\left[\mathrm{2}{b}^{\mathrm{4}} +{a}^{\mathrm{4}} +{c}^{\mathrm{4}} −\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){b}^{\mathrm{2}} \right]}}{\mathrm{2}} \\ $$$${l}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} \pm\sqrt{\left[\left({a}+{c}\right)^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} \right]\left[\mathrm{2}{b}^{\mathrm{2}} −\left({a}−{c}\right)^{\mathrm{2}} \right]}}{\mathrm{2}} \\ $$$${l}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} \pm\sqrt{\left({a}+\sqrt{\mathrm{2}}{b}+{c}\right)\left(−{a}+\sqrt{\mathrm{2}}{b}+{c}\right)\left({a}−\sqrt{\mathrm{2}}{b}+{c}\right)\left({a}+\sqrt{\mathrm{2}}{b}−{c}\right)}}{\mathrm{2}} \\ $$$${l}^{\mathrm{2}} =\frac{\mathrm{2}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} \pm\sqrt{\left(\mathrm{64}−\mathrm{2}×\mathrm{16}\right)\left(\mathrm{2}×\mathrm{16}−\mathrm{16}\right)}}{\mathrm{2}} \\ $$$${l}^{\mathrm{2}} =\mathrm{20}\pm\mathrm{8}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{l}=\mathrm{2}\sqrt{\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{2}}}=\mathrm{5}.\mathrm{59}\:{or}\:\mathrm{2}.\mathrm{95} \\ $$
Commented by behi83417@gmail.com last updated on 14/Nov/18
$${excellent}\:{sir}\:{mrW}.{thank}\:{you}\:{very} \\ $$$${much}. \\ $$
Commented by mr W last updated on 14/Nov/18
Commented by mr W last updated on 14/Nov/18

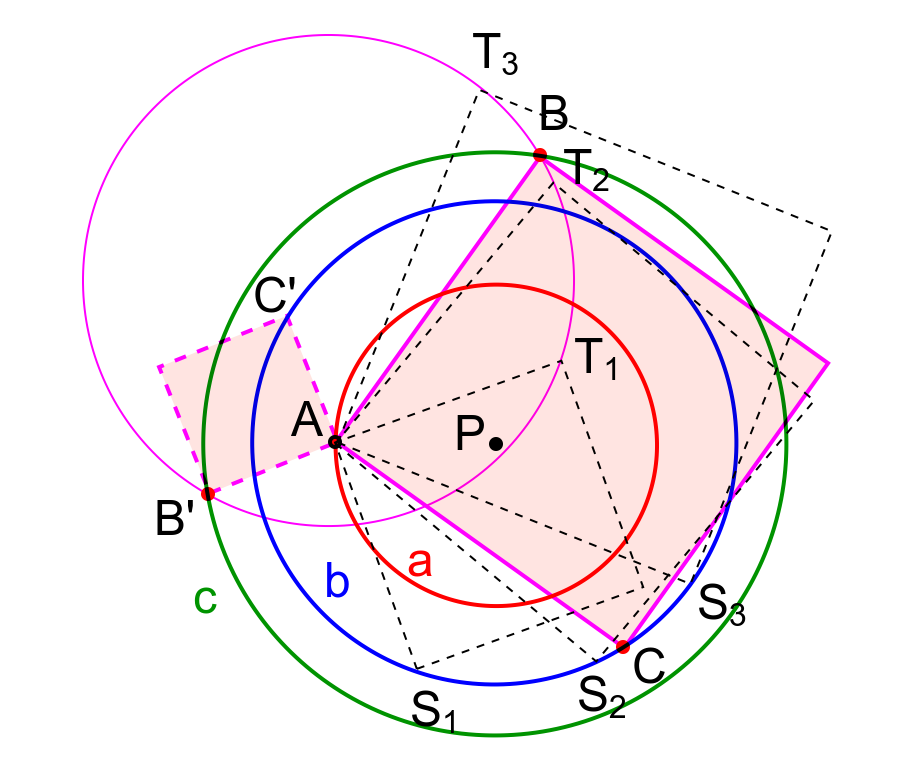
$${this}\:{is}\:{how}\:{to}\:{draw}\:{the}\:{requested}\:{square}. \\ $$$$ \\ $$$${draw}\:{three}\:{circles}\:{with}\:{radii}\:{a},{b},{c}\:{from} \\ $$$${the}\:{same}\:{center}\:{P}. \\ $$$$ \\ $$$${take}\:{a}\:{fixed}\:{point}\:{A}\:{on}\:{the}\:{first}\:{circle}. \\ $$$$ \\ $$$${select}\:{three}\:{points}\:{on}\:{the}\:{second}\:{circle}, \\ $$$${say}\:{s}\mathrm{1},{s}\mathrm{2}\:{and}\:{s}\mathrm{3}. \\ $$$$ \\ $$$${with}\:{AS}_{\mathrm{1}} \:{as}\:{side}\:{length}\:{construct}\:{a} \\ $$$${square}\:{whose}\:{vertex}\:{opposite}\:{to}\:{S}_{\mathrm{1}} \:{is}\:{T}_{\mathrm{1}} . \\ $$$${similarly}\:{we}\:{get}\:{from}\:{other}\:{two}\:{squares} \\ $$$${points}\:{T}_{\mathrm{2}} \:{and}\:{T}_{\mathrm{3}} . \\ $$$$ \\ $$$${draw}\:{a}\:{fourth}\:{circle}\:{through}\:{points} \\ $$$${T}_{\mathrm{1}} ,{T}_{\mathrm{2}} \:{and}\:{T}_{\mathrm{3}} . \\ $$$${this}\:{fourth}\:{circle}\:{intersects}\:{the}\:{third} \\ $$$${circle}\:{at}\:{two}\:{points},\:{or}\:{at}\:{one}\:{point},\:{or} \\ $$$${not}\:{at}\:{all}. \\ $$$$ \\ $$$${lets}\:{say}\:{the}\:{intersection}\:{points}\:{are} \\ $$$${B}\:{and}\:{B}'. \\ $$$${AB}\:{or}\:{AB}'\:{is}\:{the}\:{side}\:{length}\:{of}\:{the} \\ $$$${requested}\:{square}. \\ $$
Commented by behi83417@gmail.com last updated on 14/Nov/18
$${intresting}\:!{you}\:{are}\:{amazing}\:{master}. \\ $$$${thank}\:{you}\:{very}\:{much}\:{dear}. \\ $$
