
Question Number 47697 by ajfour last updated on 13/Nov/18
Commented by ajfour last updated on 13/Nov/18

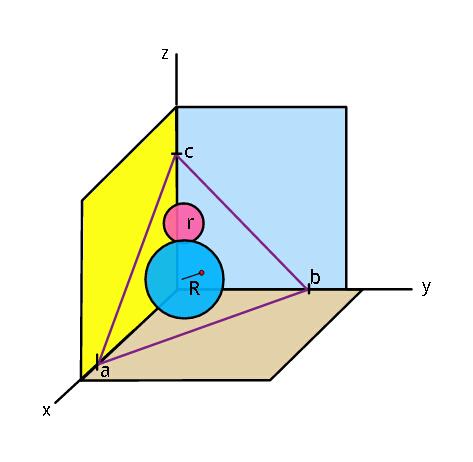
$${The}\:{blue}\:{sphere}\:{touches}\:{the} \\ $$$${xy},\:{yz},\:{zx},\:{and}\:{the}\:{triangular} \\ $$$${plate},\:{while}\:{the}\:{smaller}\:{pink} \\ $$$${sphere}\:{touches}\:{the}\:{yz},\:{zx},\:{larger} \\ $$$${sphere},\:{and}\:{the}\:{triangular}\:{plate}. \\ $$$${Find}\:{their}\:{radii}\:\boldsymbol{{R}},\:{and}\:\boldsymbol{{r}}\:{in}\:{terms} \\ $$$${of}\:\boldsymbol{{a}},\boldsymbol{{b}},{and}\:\boldsymbol{{c}}. \\ $$
Answered by ajfour last updated on 13/Nov/18
![let center of blue sphere B(R,R,R) eq. of △plate : (x/a)+(y/b)+(z/c)=1 Normal to △plate is n^� =(i^� /a)+(j^� /b)+(k^� /c) let blue sphere touch the △plate at T ⇒ r_T ^� =R(i^� +j^� +k^� )+ (R/(√((1/a^2 )+(1/b^2 )+(1/c^2 ))))((i^� /a)+(j^� /b)+(k^� /c)) let (√((1/a^2 )+(1/b^2 )+(1/c^2 ))) = ∣n^� ∣=l As r_T ^� lies on △plate ⇒ R[(1/a)(1+(1/(al)))+(1/b)(1+(1/(bl)))+(1/c)(1+(1/(cl)))]=1 ⇒ R =(1/(((1/a)+(1/b)+(1/c))+(√((1/a^2 )+(1/b^2 )+(1/c^2 ))))) Let center of pink sphere be P (r,r,z). As BP should be R+r ⇒ 2(R−r)^2 +(z−R)^2 = (R+r)^2 ⇒ 2((R/r)−1)^2 +((z/r)−(R/r))^2 = ((R/r)+1)^2 ⇒ (z/r)=(R/r)+(√(((R/r)+1)^2 −2((R/r)−1)^2 )) ......(i) And ⊥ distance of P from plate is r. Let smaller sphere touch the plate at S. r_S ^� = (ri^� +rj^� +zk^� )+ (r/l)((i^� /a)+(j^� /b)+(k^� /c)) and S lies on the plate, therefore r[(1/a)(1+(1/(al)))+(1/b)(1+(1/(bl)))+(1/c)((z/r)+(1/(cl)))]= 1 ⇒ r = (1/((1/a)+(1/b)+(1/c)((z/r))+l)) ⇒ l+(1/a)+(1/b)+(1/c)((z/r))=(1/r) Now using (i) l+(1/a)+(1/b)+(1/c)[(R/r)+(√(((R/r)+1)^2 −2((R/r)−1)^2 )) ]=(1/r) let (1/p) = l+(1/a)+(1/b) = (1/R)−(1/c) ; then (1/p)+(1/c)[(R/r)+(√(((R/r)+1)^2 −2((R/r)−1)^2 )) ]=(1/r) ⇒((R/r)+1)^2 −2((R/r)−1)^2 = [c((1/r)−(1/p))−(R/r)]^2 ⇒ ((6R)/r)−1−2((R/r))^2 =c^2 ((1/r)−(1/p))^2 −((2cR)/r)((1/r)−(1/p)) let (1/r) = t t^2 (c^2 −2cR+2R^2 )−t(((2c^2 )/p)+((2cR)/p)−6R) +((c^2 /p^2 )+1) = 0 __________________________ ⇒ (1/r) = ((((c^2 /p)+((cR)/p)−3R)±(√(((c^2 /p)+((cR)/p)−3R)^2 −(c^2 −2cR+2R^2 )((c^2 /p^2 )+1))))/(c^2 −2cR+2R^2 )) with (1/p) =(1/a)+(1/b)+(√((1/a^2 )+(1/b^2 )+(1/c^2 ))) and R =(1/(((1/a)+(1/b)+(1/c))+(√((1/a^2 )+(1/b^2 )+(1/c^2 ))))) . __________________________](Q47699.png)
$${let}\:{center}\:{of}\:{blue}\:{sphere} \\ $$$${B}\left({R},{R},{R}\right) \\ $$$${eq}.\:{of}\:\bigtriangleup{plate}\::\:\:\:\frac{{x}}{{a}}+\frac{{y}}{{b}}+\frac{{z}}{{c}}=\mathrm{1} \\ $$$${Normal}\:{to}\:\bigtriangleup{plate}\:{is} \\ $$$$\:\:\:\:\bar {{n}}=\frac{\hat {{i}}}{{a}}+\frac{\hat {{j}}}{{b}}+\frac{\hat {{k}}}{{c}} \\ $$$${let}\:{blue}\:{sphere}\:{touch}\:{the}\:\bigtriangleup{plate} \\ $$$${at}\:{T}\: \\ $$$$\Rightarrow\:\bar {{r}}_{{T}} ={R}\left(\hat {{i}}+\hat {{j}}+\hat {{k}}\right)+ \\ $$$$\:\:\:\:\:\:\frac{{R}}{\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}}\left(\frac{\hat {{i}}}{{a}}+\frac{\hat {{j}}}{{b}}+\frac{\hat {{k}}}{{c}}\right) \\ $$$${let}\:\:\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}\:=\:\mid\bar {{n}}\mid={l} \\ $$$${As}\:\bar {{r}}_{{T}} \:{lies}\:{on}\:\bigtriangleup{plate} \\ $$$$\Rightarrow\:{R}\left[\frac{\mathrm{1}}{{a}}\left(\mathrm{1}+\frac{\mathrm{1}}{{al}}\right)+\frac{\mathrm{1}}{{b}}\left(\mathrm{1}+\frac{\mathrm{1}}{{bl}}\right)+\frac{\mathrm{1}}{{c}}\left(\mathrm{1}+\frac{\mathrm{1}}{{cl}}\right)\right]=\mathrm{1} \\ $$$$\Rightarrow\:{R}\:=\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)+\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}} \\ $$$${Let}\:{center}\:{of}\:{pink}\:{sphere}\:{be} \\ $$$$\:\:{P}\:\left({r},{r},{z}\right). \\ $$$${As}\:{BP}\:{should}\:{be}\:{R}+{r}\:\Rightarrow \\ $$$$\:\:\mathrm{2}\left({R}−{r}\right)^{\mathrm{2}} +\left({z}−{R}\right)^{\mathrm{2}} =\:\left({R}+{r}\right)^{\mathrm{2}} \:\: \\ $$$$\Rightarrow\:\mathrm{2}\left(\frac{{R}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{{z}}{{r}}−\frac{{R}}{{r}}\right)^{\mathrm{2}} =\:\left(\frac{{R}}{{r}}+\mathrm{1}\right)^{\mathrm{2}} \: \\ $$$$\Rightarrow\:\:\frac{{z}}{{r}}=\frac{{R}}{{r}}+\sqrt{\left(\frac{{R}}{{r}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{R}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......\left({i}\right) \\ $$$${And} \\ $$$$\:\:\:\bot\:{distance}\:{of}\:{P}\:{from}\:{plate}\:{is}\:{r}. \\ $$$${Let}\:{smaller}\:{sphere}\:{touch}\:{the} \\ $$$${plate}\:{at}\:{S}. \\ $$$$\:\:\bar {{r}}_{{S}} \:=\:\left({r}\hat {{i}}+{r}\hat {{j}}+{z}\hat {{k}}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{{r}}{{l}}\left(\frac{\hat {{i}}}{{a}}+\frac{\hat {{j}}}{{b}}+\frac{\hat {{k}}}{{c}}\right) \\ $$$${and}\:{S}\:{lies}\:{on}\:{the}\:{plate},\:{therefore} \\ $$$${r}\left[\frac{\mathrm{1}}{{a}}\left(\mathrm{1}+\frac{\mathrm{1}}{{al}}\right)+\frac{\mathrm{1}}{{b}}\left(\mathrm{1}+\frac{\mathrm{1}}{{bl}}\right)+\frac{\mathrm{1}}{{c}}\left(\frac{{z}}{{r}}+\frac{\mathrm{1}}{{cl}}\right)\right]=\:\mathrm{1} \\ $$$$\Rightarrow\:\:{r}\:=\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\left(\frac{{z}}{{r}}\right)+{l}} \\ $$$$\Rightarrow\:\:{l}+\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\left(\frac{{z}}{{r}}\right)=\frac{\mathrm{1}}{{r}} \\ $$$${Now}\:{using}\:\left({i}\right) \\ $$$$\:\:\:{l}+\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\left[\frac{{R}}{{r}}+\sqrt{\left(\frac{{R}}{{r}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{R}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} }\:\right]=\frac{\mathrm{1}}{{r}} \\ $$$${let}\:\:\:\frac{\mathrm{1}}{{p}}\:=\:{l}+\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\:=\:\frac{\mathrm{1}}{{R}}−\frac{\mathrm{1}}{{c}}\:;\:{then} \\ $$$$\:\:\:\:\frac{\mathrm{1}}{{p}}+\frac{\mathrm{1}}{{c}}\left[\frac{{R}}{{r}}+\sqrt{\left(\frac{{R}}{{r}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{R}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} }\:\right]=\frac{\mathrm{1}}{{r}} \\ $$$$\Rightarrow\left(\frac{{R}}{{r}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{R}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} \:=\:\left[{c}\left(\frac{\mathrm{1}}{{r}}−\frac{\mathrm{1}}{{p}}\right)−\frac{{R}}{{r}}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{6}{R}}{{r}}−\mathrm{1}−\mathrm{2}\left(\frac{{R}}{{r}}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{r}}−\frac{\mathrm{1}}{{p}}\right)^{\mathrm{2}} −\frac{\mathrm{2}{cR}}{{r}}\left(\frac{\mathrm{1}}{{r}}−\frac{\mathrm{1}}{{p}}\right) \\ $$$${let}\:\:\frac{\mathrm{1}}{{r}}\:=\:{t} \\ $$$$\:{t}^{\mathrm{2}} \left({c}^{\mathrm{2}} −\mathrm{2}{cR}+\mathrm{2}{R}^{\mathrm{2}} \right)−{t}\left(\frac{\mathrm{2}{c}^{\mathrm{2}} }{{p}}+\frac{\mathrm{2}{cR}}{{p}}−\mathrm{6}{R}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\frac{{c}^{\mathrm{2}} }{{p}^{\mathrm{2}} }+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{r}}\:=\:\frac{\left(\frac{{c}^{\mathrm{2}} }{{p}}+\frac{{cR}}{{p}}−\mathrm{3}{R}\right)\pm\sqrt{\left(\frac{{c}^{\mathrm{2}} }{{p}}+\frac{{cR}}{{p}}−\mathrm{3}{R}\right)^{\mathrm{2}} −\left({c}^{\mathrm{2}} −\mathrm{2}{cR}+\mathrm{2}{R}^{\mathrm{2}} \right)\left(\frac{{c}^{\mathrm{2}} }{{p}^{\mathrm{2}} }+\mathrm{1}\right)}}{{c}^{\mathrm{2}} −\mathrm{2}{cR}+\mathrm{2}{R}^{\mathrm{2}} } \\ $$$$\:{with}\:\:\:\frac{\mathrm{1}}{{p}}\:=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }} \\ $$$${and}\:\:\:{R}\:=\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)+\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}}\:\:. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$
Commented by mr W last updated on 13/Nov/18
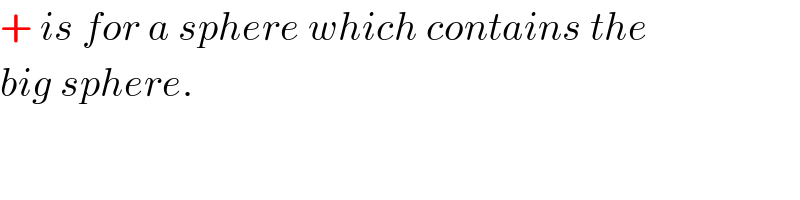
$$+\:{is}\:{for}\:{a}\:{sphere}\:{which}\:{contains}\:{the} \\ $$$${big}\:{sphere}. \\ $$
Commented by ajfour last updated on 13/Nov/18
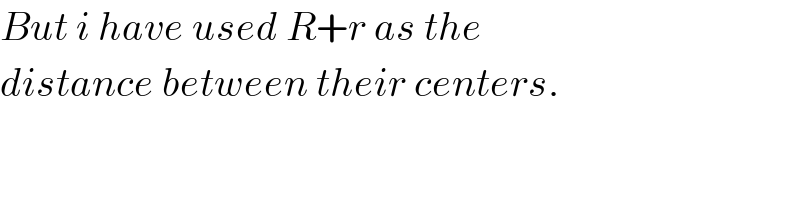
$${But}\:{i}\:{have}\:{used}\:{R}+{r}\:{as}\:{the} \\ $$$${distance}\:{between}\:{their}\:{centers}. \\ $$
Commented by mr W last updated on 13/Nov/18

$${I}\:{was}\:{wrong}\:{sir}.\:{It}\:{is}\:{for}\:{the}\:{sphere} \\ $$$${outside}.\:{This}\:{sphere}\:{touches}\:{the}\:{big} \\ $$$${one}\:{and}\:{the}\:{inclined}\:{plane}\:{at}\:{the}\:{same} \\ $$$${point}. \\ $$
Commented by MJS last updated on 14/Nov/18

$$\mathrm{just}\:\mathrm{think}\:\mathrm{what}\:\mathrm{you}\:\mathrm{set}\:\mathrm{up}\:\mathrm{before}.\:\mathrm{you}'\mathrm{ve}\:\mathrm{been} \\ $$$$\mathrm{looking}\:\mathrm{for}\:\mathrm{spheres}\:\mathrm{touching}\:\mathrm{the}\:\mathrm{blue}\:\mathrm{sphere}, \\ $$$$\mathrm{the}\:\mathrm{triangular}\:\mathrm{plate}\:\mathrm{and}\:\mathrm{the}\:\mathrm{two}\:\mathrm{walls}.\:\mathrm{the} \\ $$$$\mathrm{formulas}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{triangular}\:\mathrm{plate} \\ $$$$\mathrm{ends}\:\mathrm{at}\:\mathrm{the}\:\mathrm{floor}\:\mathrm{and}\:\mathrm{walls}\:\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{plane} \\ $$$$\Rightarrow\:\mathrm{one}\:\mathrm{sphere}\:\mathrm{is}\:\mathrm{the}\:\mathrm{pink}\:\mathrm{one}\:\mathrm{in}\:\mathrm{your}\:\mathrm{picture}, \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{one}'\mathrm{s}\:\mathrm{under}\:\mathrm{the}\:\mathrm{blue}\:\mathrm{one},\:\mathrm{it}'\mathrm{s}\:\mathrm{bigger} \\ $$$$\mathrm{than}\:\mathrm{the}\:\mathrm{blue}\:\mathrm{one}\:\mathrm{and}\:\mathrm{still}\:\mathrm{touching}\:\mathrm{the}\:\mathrm{two} \\ $$$$\mathrm{walls}\:\mathrm{and}\:−\:\mathrm{under}\:\mathrm{the}\:\mathrm{floor}\:−\:\mathrm{the}\:\mathrm{plane}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{triangular}\:\mathrm{plate} \\ $$$$\mathrm{you}\:\mathrm{gave}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{for}\:\frac{\mathrm{1}}{{r}},\:{r}\:\mathrm{will}\:\mathrm{be}\:\mathrm{greater} \\ $$$$\mathrm{with}\:\mathrm{the}\:−\:\mathrm{and}\:\mathrm{smaller}\:\mathrm{with}\:\mathrm{the}\:+ \\ $$
Commented by ajfour last updated on 14/Nov/18
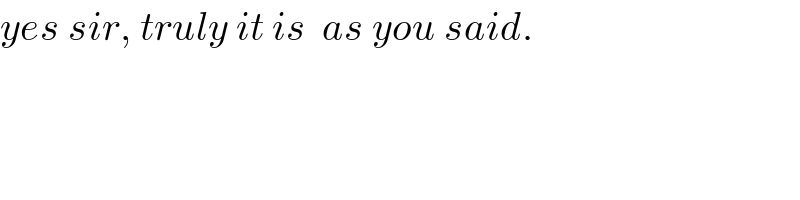
$${yes}\:{sir},\:{truly}\:{it}\:{is}\:\:{as}\:{you}\:{said}. \\ $$
