Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 47449 by ajfour last updated on 10/Nov/18

Commented by ajfour last updated on 10/Nov/18

Find the area of the shadow of the right circular cone (not including its base area). S is a point source of light, at a distance d from center of base of cone, at a height H.

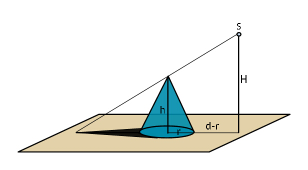
$${Find}\:{the}\:{area}\:{of}\:{the}\:{shadow}\:{of} \\ $$$${the}\:{right}\:{circular}\:{cone}\:\left({not}\right. \\ $$$$\left.{including}\:{its}\:{base}\:{area}\right). \\ $$$${S}\:{is}\:{a}\:{point}\:{source}\:{of}\:{light},\:{at} \\ $$$${a}\:{distance}\:{d}\:{from}\:{center}\:{of} \\ $$$${base}\:{of}\:{cone},\:{at}\:{a}\:{height}\:{H}. \\ $$

Answered by mr W last updated on 10/Nov/18

Commented by mr W last updated on 10/Nov/18

((e+d)/e)=(H/h) ⇒e=((hd)/(H−h)) cos θ=(r/e)=((r(H−h))/(hd)) ⇒θ=cos^(−1) ((r(H−h))/(hd)) sin θ=((√(h^2 d^2 −r^2 (H−h)^2 ))/(hd)) A_(shadow) =re sin θ−θπ=((rhd)/(H−h))×((√(h^2 d^2 −r^2 (H−h)^2 ))/(hd))−θr^2 ⇒A_(shadow) =((r(√(h^2 d^2 −r^2 (H−h)^2 )))/(H−d))−r^2 cos^(−1) ((r(H−h))/(hd))

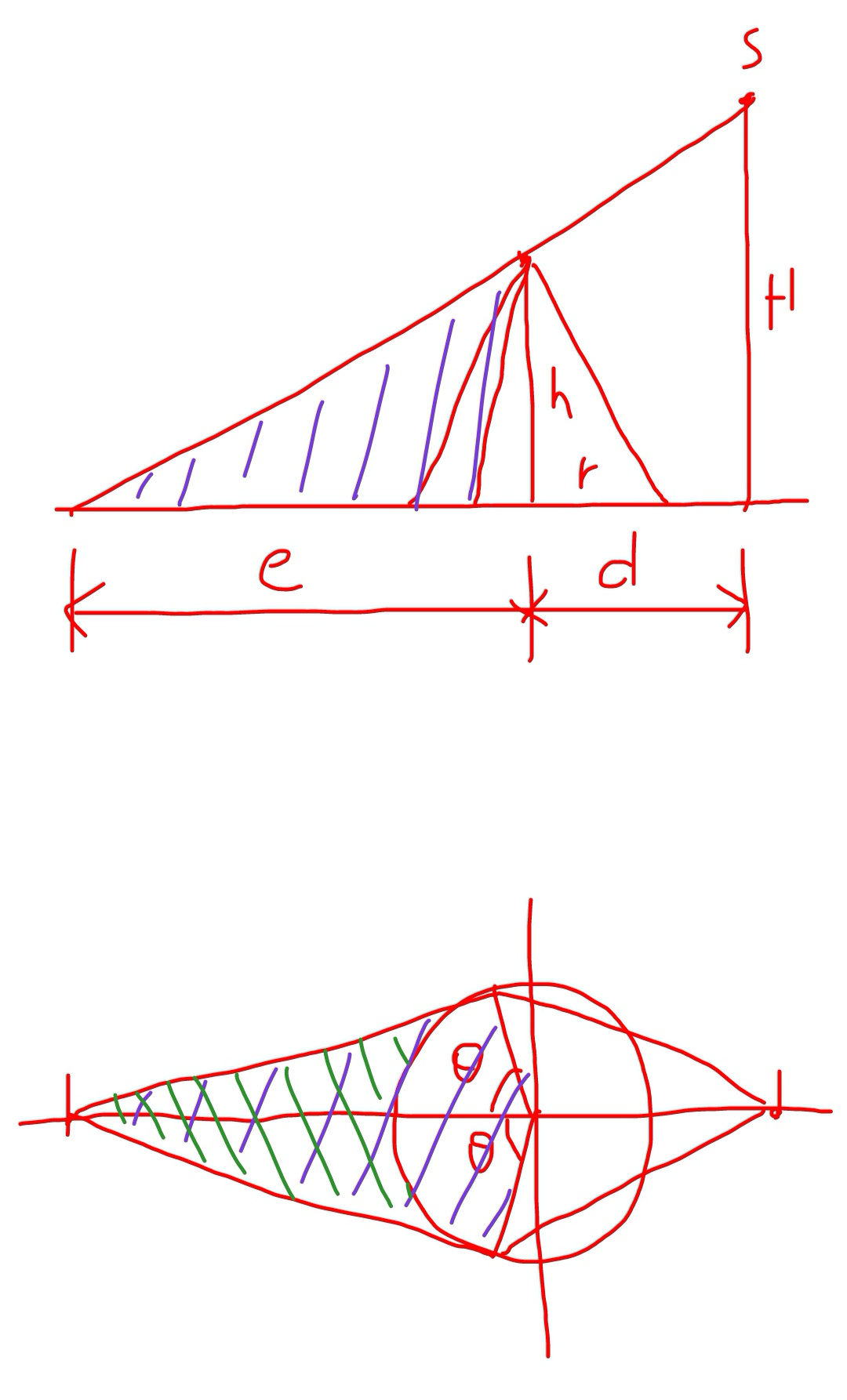
$$\frac{{e}+{d}}{{e}}=\frac{{H}}{{h}} \\ $$$$\Rightarrow{e}=\frac{{hd}}{{H}−{h}} \\ $$$$\mathrm{cos}\:\theta=\frac{{r}}{{e}}=\frac{{r}\left({H}−{h}\right)}{{hd}} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{{r}\left({H}−{h}\right)}{{hd}} \\ $$$$\mathrm{sin}\:\theta=\frac{\sqrt{{h}^{\mathrm{2}} {d}^{\mathrm{2}} −{r}^{\mathrm{2}} \left({H}−{h}\right)^{\mathrm{2}} }}{{hd}} \\ $$$${A}_{{shadow}} ={re}\:\mathrm{sin}\:\theta−\theta\pi=\frac{{rhd}}{{H}−{h}}×\frac{\sqrt{{h}^{\mathrm{2}} {d}^{\mathrm{2}} −{r}^{\mathrm{2}} \left({H}−{h}\right)^{\mathrm{2}} }}{{hd}}−\theta{r}^{\mathrm{2}} \\ $$$$\Rightarrow{A}_{{shadow}} =\frac{{r}\sqrt{{h}^{\mathrm{2}} {d}^{\mathrm{2}} −{r}^{\mathrm{2}} \left({H}−{h}\right)^{\mathrm{2}} }}{{H}−{d}}−{r}^{\mathrm{2}} \mathrm{cos}^{−\mathrm{1}} \frac{{r}\left({H}−{h}\right)}{{hd}} \\ $$

Commented by ajfour last updated on 10/Nov/18

Thank you Sir.

$${Thank}\:{you}\:{Sir}.\: \\ $$

Commented by mr W last updated on 10/Nov/18

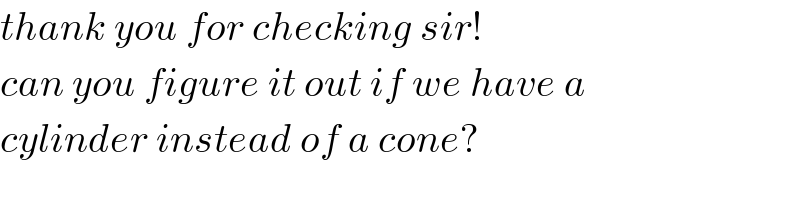
thank you for checking sir! can you figure it out if we have a cylinder instead of a cone?

$${thank}\:{you}\:{for}\:{checking}\:{sir}! \\ $$$${can}\:{you}\:{figure}\:{it}\:{out}\:{if}\:{we}\:{have}\:{a} \\ $$$${cylinder}\:{instead}\:{of}\:{a}\:{cone}? \\ $$

Commented by ajfour last updated on 10/Nov/18

Commented by ajfour last updated on 10/Nov/18

cant figure properly, not sure, Sir.

$${cant}\:{figure}\:{properly},\:{not}\:{sure}, \\ $$$${Sir}. \\ $$

Commented by MrW3 last updated on 11/Nov/18

image is nice and correct. please solve it sir.

$${image}\:{is}\:{nice}\:{and}\:{correct}. \\ $$$${please}\:{solve}\:{it}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com