Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 47401 by Aditya789 last updated on 09/Nov/18

Commented by maxmathsup by imad last updated on 10/Nov/18

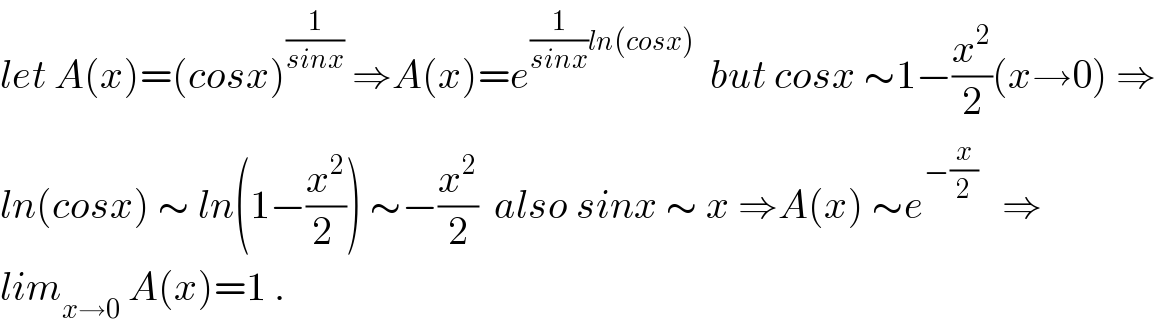
let A(x)=(cosx)^(1/(sinx)) ⇒A(x)=e^((1/(sinx))ln(cosx)) but cosx ∼1−(x^2 /2)(x→0) ⇒ ln(cosx) ∼ ln(1−(x^2 /(2 ))) ∼−(x^2 /2) also sinx ∼ x ⇒A(x) ∼e^(−(x/2)) ⇒ lim_(x→0) A(x)=1 .

$${let}\:{A}\left({x}\right)=\left({cosx}\right)^{\frac{\mathrm{1}}{{sinx}}} \:\Rightarrow{A}\left({x}\right)={e}^{\frac{\mathrm{1}}{{sinx}}{ln}\left({cosx}\right)} \:\:{but}\:{cosx}\:\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$${ln}\left({cosx}\right)\:\sim\:{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}\:}\right)\:\sim−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:{also}\:{sinx}\:\sim\:{x}\:\Rightarrow{A}\left({x}\right)\:\sim{e}^{−\frac{{x}}{\mathrm{2}}} \:\:\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:{A}\left({x}\right)=\mathrm{1}\:. \\ $$

Answered by ajfour last updated on 09/Nov/18

= lim_(x→0) [1−(1−cos x)]^(1/sin x) =lim_(x→0) {[1−2sin^2 (x/2)]^(−1/2sin^2 (x/2)) }^(−((2sin^2 (x/2))/(2sin (x/2)cos (x/2)))) = lim_(x→0) e^(−tan (x/2)) = 1 .

$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{1}−\left(\mathrm{1}−\mathrm{cos}\:{x}\right)\right]^{\mathrm{1}/\mathrm{sin}\:{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\left[\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right]^{−\mathrm{1}/\mathrm{2sin}\:^{\mathrm{2}} \left({x}/\mathrm{2}\right)} \right\}^{−\frac{\mathrm{2sin}\:^{\mathrm{2}} \left({x}/\mathrm{2}\right)}{\mathrm{2sin}\:\left({x}/\mathrm{2}\right)\mathrm{cos}\:\left({x}/\mathrm{2}\right)}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{e}^{−\mathrm{tan}\:\left({x}/\mathrm{2}\right)} \:=\:\mathrm{1}\:. \\ $$

Answered by rahul 19 last updated on 11/Nov/18

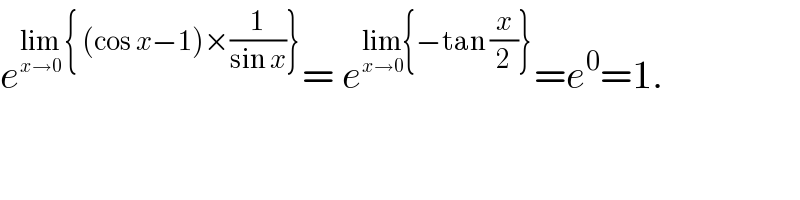
e^(lim_(x→0) { (cos x−1)×(1/(sin x))}) = e^(lim_(x→0) {−tan (x/2)}) =e^0 =1.

$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left\{\:\left(\mathrm{cos}\:{x}−\mathrm{1}\right)×\frac{\mathrm{1}}{\mathrm{sin}\:{x}}\right\}} =\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{−\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right\}} ={e}^{\mathrm{0}} =\mathrm{1}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com