Question and Answers Forum

All Questions      Topic List

Set Theory Questions

Previous in All Question      Next in All Question      

Previous in Set Theory      Next in Set Theory      

Question Number 47354 by behi83417@gmail.com last updated on 08/Nov/18

Commented by behi83417@gmail.com last updated on 08/Nov/18

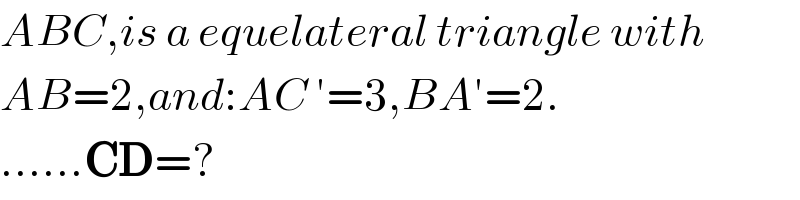
ABC,is a equelateral triangle with AB=2,and:AC ′=3,BA′=2. ......CD=?

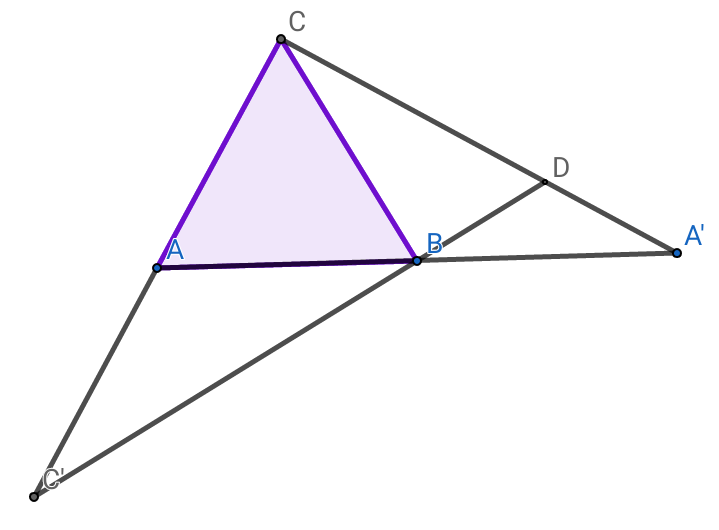
$${ABC},{is}\:{a}\:{equelateral}\:{triangle}\:{with} \\ $$$${AB}=\mathrm{2},{and}:{AC}\:'=\mathrm{3},{BA}'=\mathrm{2}. \\ $$$$......\boldsymbol{\mathrm{CD}}=? \\ $$

Commented by ajfour last updated on 09/Nov/18

Commented by ajfour last updated on 09/Nov/18

γ = 30° ⇒ ∠C = 90° A′C =(√(4^2 −2^2 )) = 2(√3) ...(i) From △BCD ((sin β)/2)=((sin γ)/(BD)) & From △BDA′ ((sin γ)/(BD)) = ((sin (β−γ))/(A′D)) ⇒ A′D = ((3sin (β−γ))/(sin β)) ....(ii) From △CC ′D ((sin α)/(CD)) = ((cos β)/(CD))=((sin β)/5) ⇒ tan β = (5/(CD)) ...(iii) Using (i), (ii) for CD+A′D = A′C ⇒ CD+((3sin (β−γ))/(sin β)) = 2(√3) ...(I) let CD = x Then using (iii)&(I) x+3(cos γ−((sin γ)/(tan β)))=2(√3) ⇒ x+3(((√3)/2)−(x/(10)))=2(√3) or ((7x)/(10)) = ((√3)/2) ⇒ x = CD = ((5(√3))/7) .

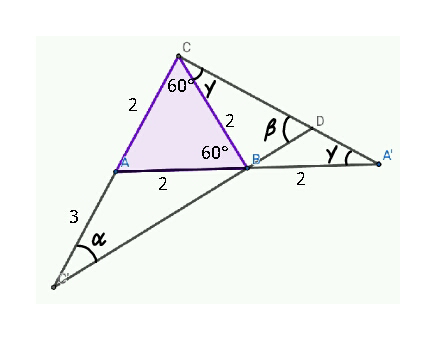
$$\:\:\gamma\:=\:\mathrm{30}°\:\:\:\Rightarrow\:\angle{C}\:=\:\mathrm{90}° \\ $$$${A}'{C}\:=\sqrt{\mathrm{4}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\:=\:\mathrm{2}\sqrt{\mathrm{3}}\:\:\:...\left({i}\right) \\ $$$${From}\:\bigtriangleup{BCD} \\ $$$$\:\frac{\mathrm{sin}\:\beta}{\mathrm{2}}=\frac{\mathrm{sin}\:\gamma}{{BD}}\:\:\&\:\:{From}\:\bigtriangleup{BDA}' \\ $$$$\:\frac{\mathrm{sin}\:\gamma}{{BD}}\:=\:\frac{\mathrm{sin}\:\left(\beta−\gamma\right)}{{A}'{D}} \\ $$$$\Rightarrow\:\:\:{A}'{D}\:=\:\frac{\mathrm{3sin}\:\left(\beta−\gamma\right)}{\mathrm{sin}\:\beta}\:\:\:....\left({ii}\right) \\ $$$${From}\:\bigtriangleup{CC}\:'{D} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{CD}}\:=\:\frac{\mathrm{cos}\:\beta}{{CD}}=\frac{\mathrm{sin}\:\beta}{\mathrm{5}}\: \\ $$$$\Rightarrow\:\:\:\mathrm{tan}\:\beta\:=\:\frac{\mathrm{5}}{{CD}}\:\:\:\:...\left({iii}\right) \\ $$$${Using}\:\:\left({i}\right),\:\left({ii}\right)\:{for} \\ $$$$\:\:\:{CD}+{A}'{D}\:=\:{A}'{C} \\ $$$$\Rightarrow\:\:{CD}+\frac{\mathrm{3sin}\:\left(\beta−\gamma\right)}{\mathrm{sin}\:\beta}\:=\:\mathrm{2}\sqrt{\mathrm{3}}\:\:\:...\left({I}\right) \\ $$$${let}\:\:{CD}\:=\:{x} \\ $$$${Then}\:{using}\:\left({iii}\right)\&\left({I}\right) \\ $$$$\:\:\:\:{x}+\mathrm{3}\left(\mathrm{cos}\:\gamma−\frac{\mathrm{sin}\:\gamma}{\mathrm{tan}\:\beta}\right)=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\:{x}+\mathrm{3}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{{x}}{\mathrm{10}}\right)=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${or}\:\:\:\:\:\frac{\mathrm{7}{x}}{\mathrm{10}}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{x}\:=\:{CD}\:=\:\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{7}}\:.\: \\ $$

Commented by behi83417@gmail.com last updated on 09/Nov/18

sir Ajfour!thank you very much for nice work.god bless you sir.

$${sir}\:{Ajfour}!{thank}\:{you}\:{very}\:{much} \\ $$$${for}\:{nice}\:{work}.{god}\:{bless}\:{you}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com