
Question and Answers Forum
Question Number 47342 by ajfour last updated on 08/Nov/18

Commented by ajfour last updated on 08/Nov/18

Answered by MrW3 last updated on 08/Nov/18
![a_1 =acceleration of wedge (→) a_2 =acceleration of small block on ground (←) a_3 =acceleration of small block on wedge (↙) a_3 =a_1 +a_2 T=m_o a_2 mg sin β−T=m(a_3 −a_1 cos β)=m[(1−cos β)a_1 +a_2 ] mg cos β−N=ma_1 sin β ⇒N=m(g cos β−a_1 sin β) T−T cos β+N sin β=Ma_1 T(1−cos β)+m(g cos β−a_1 sin β)sin β=Ma_1 m_0 a_2 (1−cos β)+m(g cos β−a_1 sin β)sin β=Ma_1 ⇒(M+m sin^2 β)a_1 −m_0 (1−cos β)a_2 =mg cos βsin β ...(i) ⇒m(1−cos β)a_1 +(m+m_0 )a_2 =mg sin β ...(ii) ⇒[(m+m_0 )(M+m sin^2 β)+m_0 m(1−cos β)^2 ]a_2 =mg sin β[M+m(1−cos β)] ⇒a_2 =((mg sin β[M+m(1−cos β)])/((m+m_0 )(M+m sin^2 β)+m_0 m(1−cos β)^2 )) ⇒T=((m_0 m[M+m(1−cos β)]g sin β)/((m+m_0 )(M+m sin^2 β)+m_0 m(1−cos β)^2 ))](Q47352.png)
Commented by ajfour last updated on 09/Nov/18
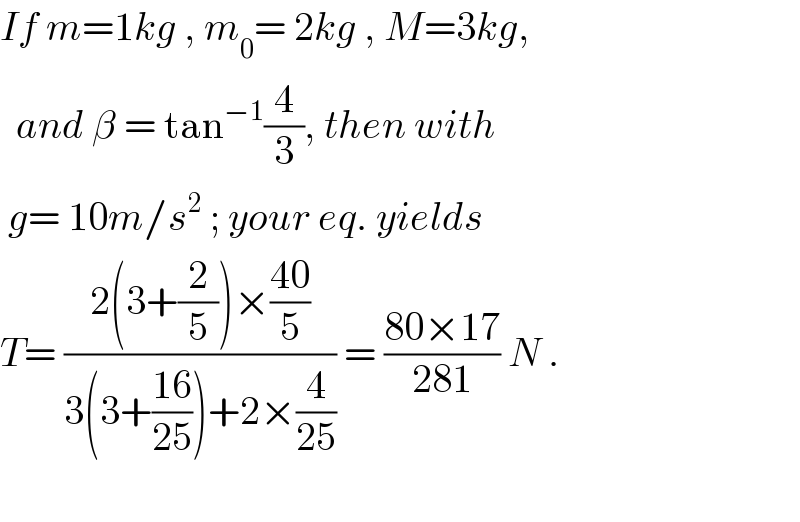
Commented by ajfour last updated on 09/Nov/18

Answered by ajfour last updated on 09/Nov/18
![T=(M+m)A−m(A+a_0 )cos β = m_0 a_0 mgsin β−T = m[(A+a_0 )−Acos β] Adding ⇒ mgsin β=ma_0 (1−cos β)+MA +2mA(1−cos β) ⇒ mgsin β=ma_0 (1−cos β) +A[M+2m(1−cos β)] ⇒ mgsin β=ma_0 (1−cos β) +((a_0 (m_0 +mcos β)[M+2m(1−cos β))/(M+m(1−cos β))) a_0 =((mgsin β[M+m(1−cos β)])/(m(1−cos β)[M+m(1−cos β)]+(m_0 +mcos β)[M+2m(1−cos β)])) T= ((mm_0 gsin β[M+m(1−cos β)])/(m(1−cos β)[M+m(1−cos β)]+(m_0 +mcos β)[M+2m(1−cos β)])) If m=1kg , m_0 = 2kg , M=3kg and β = tan^(−1) (4/3) T = ((20×(4/5)(3+(2/5)))/((2/5)(3+(2/5))+(2+(3/5))(3+(4/5)))) = ((80×17)/(34+13×19)) = ((80×17)/(281)) N .](Q47372.png)
