Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 47316 by peter frank last updated on 08/Nov/18

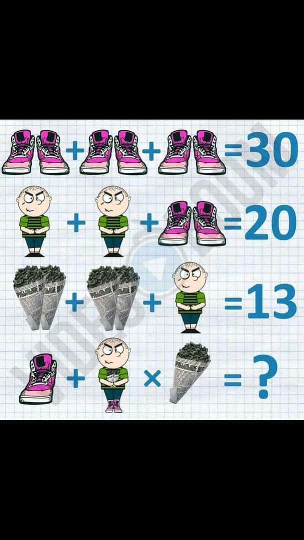
Commented by math1967 last updated on 08/Nov/18

man contains 2shoes and 2paper

$${man}\:\:{contains}\:\mathrm{2}{shoes}\:{and}\:\mathrm{2}{paper} \\ $$

Commented by MJS last updated on 08/Nov/18

(1) try to buy only the right shoe (s_r ); you′ll find you have to buy the pair ⇒ s_r =s_r +s_l =s_l . but here we have s_r s_l +s_r s_l +s_r s_l =30 ⇒ s_r s_l =10 so this might get hard to solve (2) two boys will cause much more trouble than one boy (b), I have 4 children, 3 boys and one girl, together they caused ≈11.4066 units of trouble, the exact formula is trouble=(π^(boys) /e^(girls) ), in our case π^2 ≈9.86960 ⇒ b+b=9.86960b ⇒ 9.86960b+s_r s_l =20 (3) buying two cones you will probably get %, so c+c<2c and probably c+c<c^2 ⇒ c>2 c^2 +c^2 +b=13 (4) the boy now wears shoes, they rather look multiplicated again, and to get the boy′s feet out of the shoes we will have to extract the root ⇒ ((s_r s_l ))^(1/b) . a boy looking like this one wearing pink shoes only exists in somebody′s weird dreams ⇒ i((s_r s_l ))^(1/b) and he holds 2 cones, s_r +i((s_r s_l ))^(1/b) ×c^3 =? this cannot be solved using elementary calculus but using the secret formula of Ramanjuan&Ostrogradski at least we get the Shoemaker−Conestant ξ_0 =43

$$\left(\mathrm{1}\right)\:\mathrm{try}\:\mathrm{to}\:\mathrm{buy}\:\mathrm{only}\:\mathrm{the}\:\mathrm{right}\:\mathrm{shoe}\:\left({s}_{{r}} \right);\:\mathrm{you}'\mathrm{ll}\:\mathrm{find}\:\mathrm{you} \\ $$$$\mathrm{have}\:\mathrm{to}\:\mathrm{buy}\:\mathrm{the}\:\mathrm{pair}\:\Rightarrow\:{s}_{{r}} ={s}_{{r}} +{s}_{{l}} ={s}_{{l}} .\:\mathrm{but}\:\mathrm{here} \\ $$$$\mathrm{we}\:\mathrm{have}\:{s}_{{r}} {s}_{{l}} +{s}_{{r}} {s}_{{l}} +{s}_{{r}} {s}_{{l}} =\mathrm{30}\:\Rightarrow\:{s}_{{r}} {s}_{{l}} =\mathrm{10}\:\mathrm{so}\:\mathrm{this} \\ $$$$\mathrm{might}\:\mathrm{get}\:\mathrm{hard}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{two}\:\mathrm{boys}\:\mathrm{will}\:\mathrm{cause}\:\mathrm{much}\:\mathrm{more}\:\mathrm{trouble} \\ $$$$\mathrm{than}\:\mathrm{one}\:\mathrm{boy}\:\left({b}\right),\:\mathrm{I}\:\mathrm{have}\:\mathrm{4}\:\mathrm{children},\:\mathrm{3}\:\mathrm{boys} \\ $$$$\mathrm{and}\:\mathrm{one}\:\mathrm{girl},\:\mathrm{together}\:\mathrm{they}\:\mathrm{caused}\:\approx\mathrm{11}.\mathrm{4066}\:\mathrm{units} \\ $$$$\mathrm{of}\:\mathrm{trouble},\:\mathrm{the}\:\mathrm{exact}\:\mathrm{formula}\:\mathrm{is}\:{trouble}=\frac{\pi^{{boys}} }{\mathrm{e}^{{girls}} },\:\mathrm{in} \\ $$$$\mathrm{our}\:\mathrm{case}\:\pi^{\mathrm{2}} \approx\mathrm{9}.\mathrm{86960}\:\Rightarrow\:{b}+{b}=\mathrm{9}.\mathrm{86960}{b}\:\Rightarrow \\ $$$$\mathrm{9}.\mathrm{86960}{b}+{s}_{{r}} {s}_{{l}} =\mathrm{20} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{buying}\:\mathrm{two}\:\mathrm{cones}\:\mathrm{you}\:\mathrm{will}\:\mathrm{probably}\:\mathrm{get}\:\%, \\ $$$$\mathrm{so}\:{c}+{c}<\mathrm{2}{c}\:\mathrm{and}\:\mathrm{probably}\:{c}+{c}<{c}^{\mathrm{2}} \:\Rightarrow\:{c}>\mathrm{2} \\ $$$${c}^{\mathrm{2}} +{c}^{\mathrm{2}} +{b}=\mathrm{13} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{the}\:\mathrm{boy}\:\mathrm{now}\:\mathrm{wears}\:\mathrm{shoes},\:\mathrm{they}\:\mathrm{rather} \\ $$$$\mathrm{look}\:\mathrm{multiplicated}\:\mathrm{again},\:\mathrm{and}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{boy}'\mathrm{s} \\ $$$$\mathrm{feet}\:\mathrm{out}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shoes}\:\mathrm{we}\:\mathrm{will}\:\mathrm{have}\:\mathrm{to}\:\mathrm{extract} \\ $$$$\mathrm{the}\:\mathrm{root}\:\Rightarrow\:\sqrt[{{b}}]{{s}_{{r}} {s}_{{l}} }.\:\mathrm{a}\:\mathrm{boy}\:\mathrm{looking}\:\mathrm{like}\:\mathrm{this}\:\mathrm{one} \\ $$$$\mathrm{wearing}\:\mathrm{pink}\:\mathrm{shoes}\:\mathrm{only}\:\mathrm{exists}\:\mathrm{in}\:\mathrm{somebody}'\mathrm{s} \\ $$$$\mathrm{weird}\:\mathrm{dreams}\:\Rightarrow\:\mathrm{i}\sqrt[{{b}}]{{s}_{{r}} {s}_{{l}} }\:\mathrm{and}\:\mathrm{he}\:\mathrm{holds}\:\mathrm{2}\:\mathrm{cones}, \\ $$$${s}_{{r}} +\mathrm{i}\sqrt[{{b}}]{{s}_{{r}} {s}_{{l}} }×{c}^{\mathrm{3}} =? \\ $$$$\mathrm{this}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{using}\:\mathrm{elementary} \\ $$$$\mathrm{calculus}\:\mathrm{but}\:\mathrm{using}\:\mathrm{the}\:\mathrm{secret}\:\mathrm{formula}\:\mathrm{of} \\ $$$$\mathrm{Ramanjuan\&Ostrogradski}\:\mathrm{at}\:\mathrm{least}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{the}\:\mathrm{Shoemaker}−\mathrm{Conestant}\:\xi_{\mathrm{0}} =\mathrm{43} \\ $$

Commented by behi83417@gmail.com last updated on 08/Nov/18

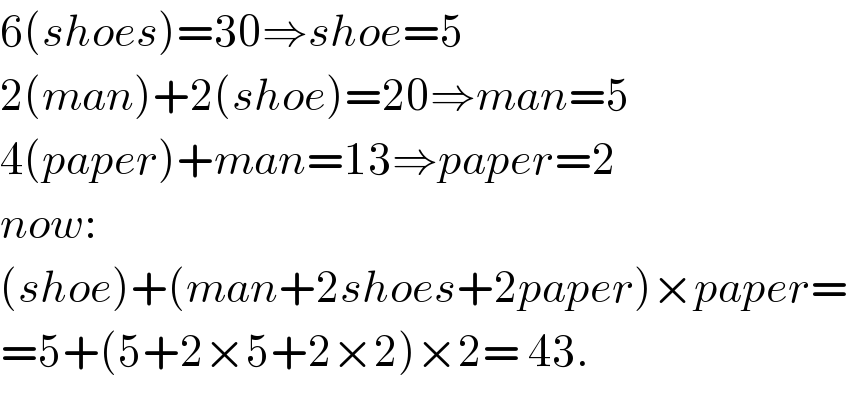
6(shoes)=30⇒shoe=5 2(man)+2(shoe)=20⇒man=5 4(paper)+man=13⇒paper=2 now: (shoe)+(man+2shoes+2paper)×paper= =5+(5+2×5+2×2)×2= 43.

$$\mathrm{6}\left({shoes}\right)=\mathrm{30}\Rightarrow{shoe}=\mathrm{5} \\ $$$$\mathrm{2}\left({man}\right)+\mathrm{2}\left({shoe}\right)=\mathrm{20}\Rightarrow{man}=\mathrm{5} \\ $$$$\mathrm{4}\left({paper}\right)+{man}=\mathrm{13}\Rightarrow{paper}=\mathrm{2} \\ $$$${now}: \\ $$$$\left({shoe}\right)+\left({man}+\mathrm{2}{shoes}+\mathrm{2}{paper}\right)×{paper}= \\ $$$$=\mathrm{5}+\left(\mathrm{5}+\mathrm{2}×\mathrm{5}+\mathrm{2}×\mathrm{2}\right)×\mathrm{2}=\:\mathrm{43}. \\ $$

Answered by ajfour last updated on 08/Nov/18

((30+20)/2)−13 .

$$\frac{\mathrm{30}+\mathrm{20}}{\mathrm{2}}−\mathrm{13}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com