Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 47179 by peter frank last updated on 05/Nov/18

Answered by tanmay.chaudhury50@gmail.com last updated on 06/Nov/18

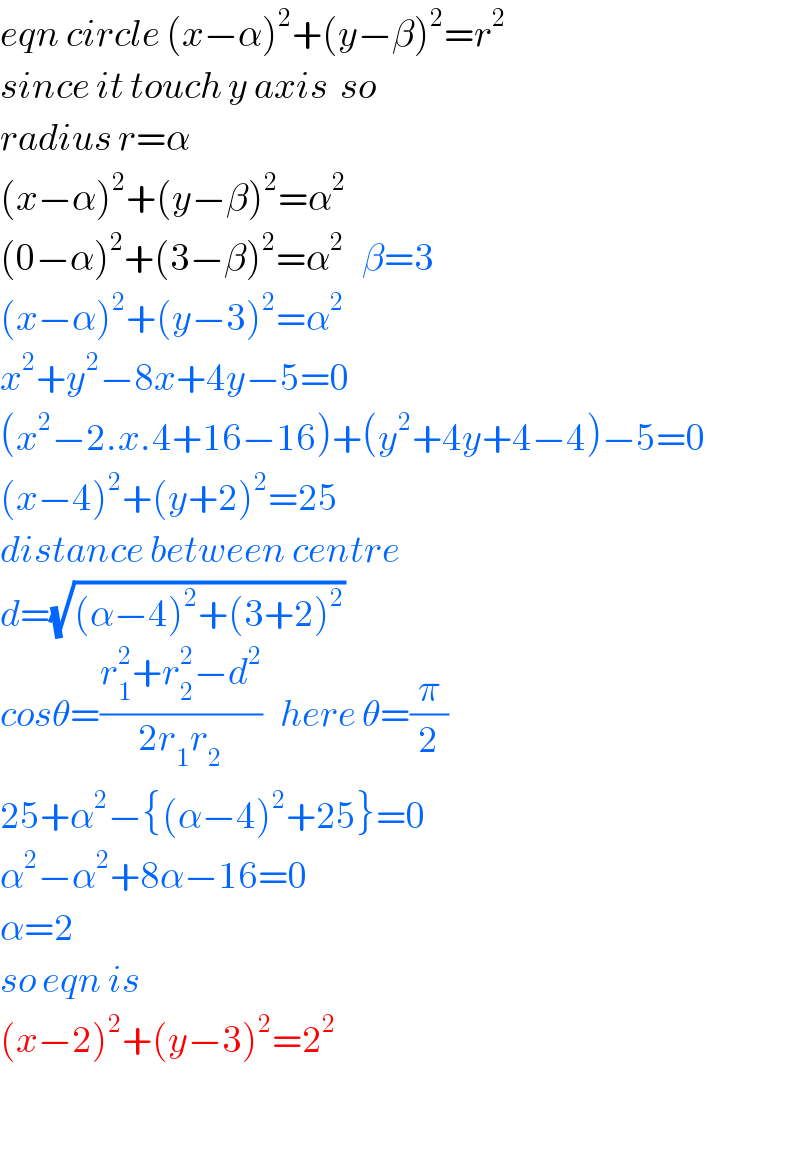
eqn circle (x−α)^2 +(y−β)^2 =r^2 since it touch y axis so radius r=α (x−α)^2 +(y−β)^2 =α^2 (0−α)^2 +(3−β)^2 =α^2 β=3 (x−α)^2 +(y−3)^2 =α^2 x^2 +y^2 −8x+4y−5=0 (x^2 −2.x.4+16−16)+(y^2 +4y+4−4)−5=0 (x−4)^2 +(y+2)^2 =25 distance between centre d=(√((α−4)^2 +(3+2)^2 )) cosθ=((r_1 ^2 +r_2 ^2 −d^2 )/(2r_1 r_2 )) here θ=(π/2) 25+α^2 −{(α−4)^2 +25}=0 α^2 −α^2 +8α−16=0 α=2 so eqn is (x−2)^2 +(y−3)^2 =2^2

$${eqn}\:{circle}\:\left({x}−\alpha\right)^{\mathrm{2}} +\left({y}−\beta\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${since}\:{it}\:{touch}\:{y}\:{axis}\:\:{so} \\ $$$${radius}\:{r}=\alpha \\ $$$$\left({x}−\alpha\right)^{\mathrm{2}} +\left({y}−\beta\right)^{\mathrm{2}} =\alpha^{\mathrm{2}} \\ $$$$\left(\mathrm{0}−\alpha\right)^{\mathrm{2}} +\left(\mathrm{3}−\beta\right)^{\mathrm{2}} =\alpha^{\mathrm{2}} \:\:\:\beta=\mathrm{3} \\ $$$$\left({x}−\alpha\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\alpha^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{4}{y}−\mathrm{5}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}.{x}.\mathrm{4}+\mathrm{16}−\mathrm{16}\right)+\left({y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{4}−\mathrm{4}\right)−\mathrm{5}=\mathrm{0} \\ $$$$\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$${distance}\:{between}\:{centre} \\ $$$${d}=\sqrt{\left(\alpha−\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{3}+\mathrm{2}\right)^{\mathrm{2}} }\: \\ $$$${cos}\theta=\frac{{r}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} −{d}^{\mathrm{2}} }{\mathrm{2}{r}_{\mathrm{1}} {r}_{\mathrm{2}} }\:\:\:{here}\:\theta=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{25}+\alpha^{\mathrm{2}} −\left\{\left(\alpha−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{25}\right\}=\mathrm{0} \\ $$$$\alpha^{\mathrm{2}} −\alpha^{\mathrm{2}} +\mathrm{8}\alpha−\mathrm{16}=\mathrm{0} \\ $$$$\alpha=\mathrm{2} \\ $$$${so}\:{eqn}\:{is} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \\ $$$$ \\ $$

Commented by peter frank last updated on 06/Nov/18

pls sir help Qn 47185

$$\mathrm{pls}\:\mathrm{sir}\:\mathrm{help}\:\mathrm{Qn}\:\mathrm{47185} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com