Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 47135 by Tawa1 last updated on 05/Nov/18

Commented by Meritguide1234 last updated on 05/Nov/18

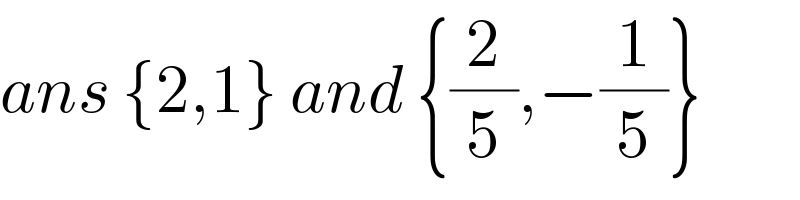
ans {2,1} and {(2/5),−(1/5)}

$${ans}\:\left\{\mathrm{2},\mathrm{1}\right\}\:{and}\:\left\{\frac{\mathrm{2}}{\mathrm{5}},−\frac{\mathrm{1}}{\mathrm{5}}\right\} \\ $$

Commented by behi83417@gmail.com last updated on 06/Nov/18

x^2 +y^2 =(1/t)⇒ { ((5x(1+t)=12)),((5y(1−t)=4)) :} ((25)/t)=((144)/((1+t)^2 ))+((16)/((1−t)^2 ))⇒ 25(1−t^2 )^2 =t[16+32t+16t^2 +144−288t+144t^2 ] 25−50t^2 +25t^4 =160t−256t^2 +160t^3 25t^4 −160t^3 +206t^2 −160t+25=0 ⇒t^4 −6.4t^3 +8.24t^2 −6.4t+1=0 ⇒t=5,0.2 t=5⇒ { ((x=((12)/(5(1+5)))=(2/5))),((y=(4/(5(1−5)))=−(1/5))) :} t=0.2⇒ { ((x=((12)/(5(1+0.2)))=2)),((y=(4/(5(1−0.2)))=1.■)) :}

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\frac{\mathrm{1}}{{t}}\Rightarrow\begin{cases}{\mathrm{5}{x}\left(\mathrm{1}+{t}\right)=\mathrm{12}}\\{\mathrm{5}{y}\left(\mathrm{1}−{t}\right)=\mathrm{4}}\end{cases} \\ $$$$\frac{\mathrm{25}}{{t}}=\frac{\mathrm{144}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }+\frac{\mathrm{16}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }\Rightarrow \\ $$$$\mathrm{25}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} ={t}\left[\mathrm{16}+\mathrm{32}{t}+\mathrm{16}{t}^{\mathrm{2}} +\mathrm{144}−\mathrm{288}{t}+\mathrm{144}{t}^{\mathrm{2}} \right] \\ $$$$\mathrm{25}−\mathrm{50}{t}^{\mathrm{2}} +\mathrm{25}{t}^{\mathrm{4}} =\mathrm{160}{t}−\mathrm{256}{t}^{\mathrm{2}} +\mathrm{160}{t}^{\mathrm{3}} \\ $$$$\mathrm{25}{t}^{\mathrm{4}} −\mathrm{160}{t}^{\mathrm{3}} +\mathrm{206}{t}^{\mathrm{2}} −\mathrm{160}{t}+\mathrm{25}=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{4}} −\mathrm{6}.\mathrm{4}{t}^{\mathrm{3}} +\mathrm{8}.\mathrm{24}{t}^{\mathrm{2}} −\mathrm{6}.\mathrm{4}{t}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{5},\mathrm{0}.\mathrm{2} \\ $$$${t}=\mathrm{5}\Rightarrow\begin{cases}{{x}=\frac{\mathrm{12}}{\mathrm{5}\left(\mathrm{1}+\mathrm{5}\right)}=\frac{\mathrm{2}}{\mathrm{5}}}\\{{y}=\frac{\mathrm{4}}{\mathrm{5}\left(\mathrm{1}−\mathrm{5}\right)}=−\frac{\mathrm{1}}{\mathrm{5}}}\end{cases} \\ $$$${t}=\mathrm{0}.\mathrm{2}\Rightarrow\begin{cases}{{x}=\frac{\mathrm{12}}{\mathrm{5}\left(\mathrm{1}+\mathrm{0}.\mathrm{2}\right)}=\mathrm{2}}\\{{y}=\frac{\mathrm{4}}{\mathrm{5}\left(\mathrm{1}−\mathrm{0}.\mathrm{2}\right)}=\mathrm{1}.\blacksquare}\end{cases} \\ $$

Commented by Tawa1 last updated on 06/Nov/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by behi83417@gmail.com last updated on 06/Nov/18

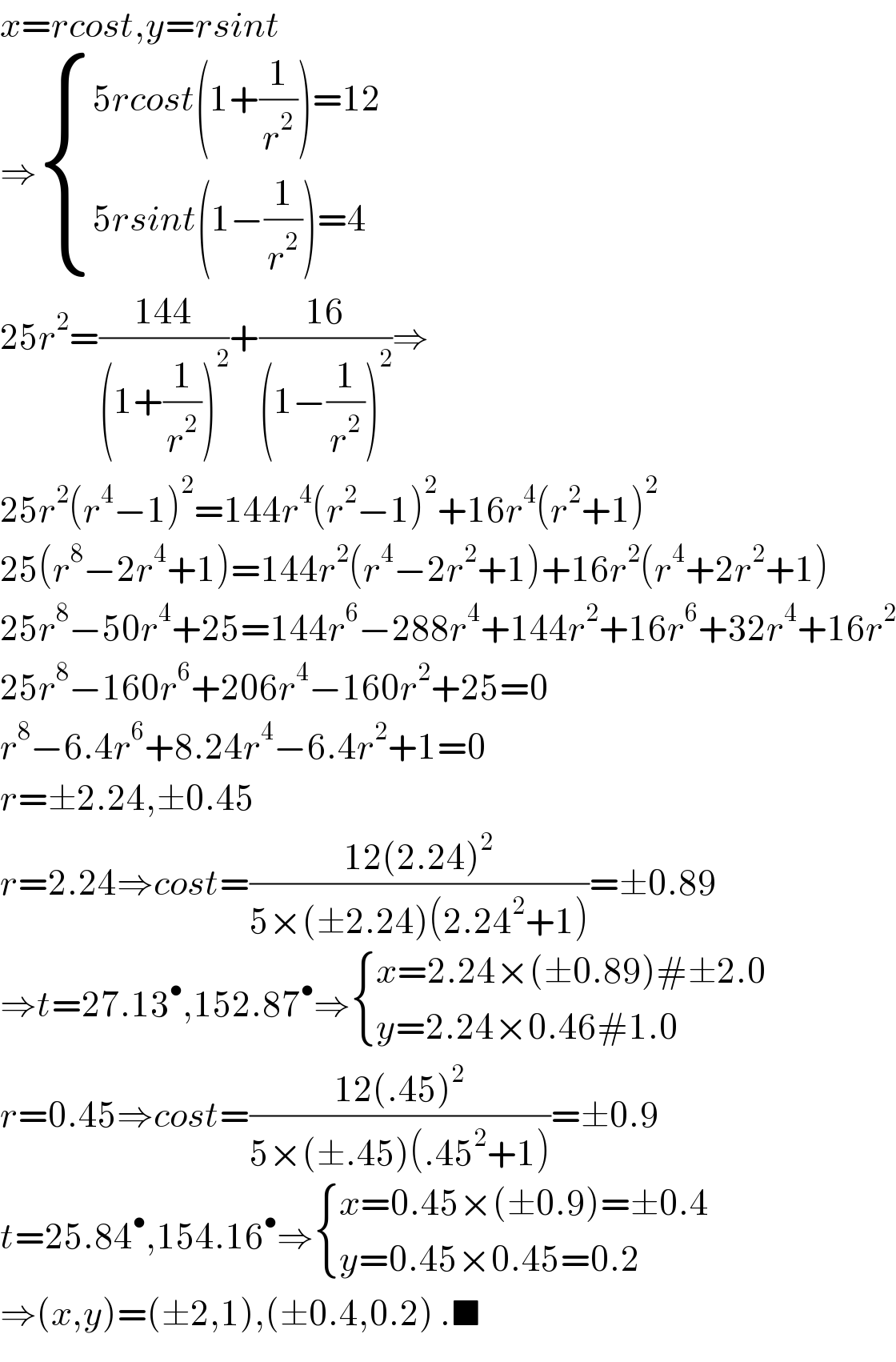
x=rcost,y=rsint ⇒ { ((5rcost(1+(1/r^2 ))=12)),((5rsint(1−(1/r^2 ))=4)) :} 25r^2 =((144)/((1+(1/r^2 ))^2 ))+((16)/((1−(1/r^2 ))^2 ))⇒ 25r^2 (r^4 −1)^2 =144r^4 (r^2 −1)^2 +16r^4 (r^2 +1)^2 25(r^8 −2r^4 +1)=144r^2 (r^4 −2r^2 +1)+16r^2 (r^4 +2r^2 +1) 25r^8 −50r^4 +25=144r^6 −288r^4 +144r^2 +16r^6 +32r^4 +16r^2 25r^8 −160r^6 +206r^4 −160r^2 +25=0 r^8 −6.4r^6 +8.24r^4 −6.4r^2 +1=0 r=±2.24,±0.45 r=2.24⇒cost=((12(2.24)^2 )/(5×(±2.24)(2.24^2 +1)))=±0.89 ⇒t=27.13^• ,152.87^• ⇒ { ((x=2.24×(±0.89)#±2.0)),((y=2.24×0.46#1.0)) :} r=0.45⇒cost=((12(.45)^2 )/(5×(±.45)(.45^2 +1)))=±0.9 t=25.84^• ,154.16^• ⇒ { ((x=0.45×(±0.9)=±0.4)),((y=0.45×0.45=0.2)) :} ⇒(x,y)=(±2,1),(±0.4,0.2) .■

$${x}={rcost},{y}={rsint} \\ $$$$\Rightarrow\begin{cases}{\mathrm{5}{rcost}\left(\mathrm{1}+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right)=\mathrm{12}}\\{\mathrm{5}{rsint}\left(\mathrm{1}−\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right)=\mathrm{4}}\end{cases} \\ $$$$\mathrm{25}{r}^{\mathrm{2}} =\frac{\mathrm{144}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right)^{\mathrm{2}} }+\frac{\mathrm{16}}{\left(\mathrm{1}−\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right)^{\mathrm{2}} }\Rightarrow \\ $$$$\mathrm{25}{r}^{\mathrm{2}} \left({r}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} =\mathrm{144}{r}^{\mathrm{4}} \left({r}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{16}{r}^{\mathrm{4}} \left({r}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{25}\left({r}^{\mathrm{8}} −\mathrm{2}{r}^{\mathrm{4}} +\mathrm{1}\right)=\mathrm{144}{r}^{\mathrm{2}} \left({r}^{\mathrm{4}} −\mathrm{2}{r}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{16}{r}^{\mathrm{2}} \left({r}^{\mathrm{4}} +\mathrm{2}{r}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\mathrm{25}{r}^{\mathrm{8}} −\mathrm{50}{r}^{\mathrm{4}} +\mathrm{25}=\mathrm{144}{r}^{\mathrm{6}} −\mathrm{288}{r}^{\mathrm{4}} +\mathrm{144}{r}^{\mathrm{2}} +\mathrm{16}{r}^{\mathrm{6}} +\mathrm{32}{r}^{\mathrm{4}} +\mathrm{16}{r}^{\mathrm{2}} \\ $$$$\mathrm{25}{r}^{\mathrm{8}} −\mathrm{160}{r}^{\mathrm{6}} +\mathrm{206}{r}^{\mathrm{4}} −\mathrm{160}{r}^{\mathrm{2}} +\mathrm{25}=\mathrm{0} \\ $$$${r}^{\mathrm{8}} −\mathrm{6}.\mathrm{4}{r}^{\mathrm{6}} +\mathrm{8}.\mathrm{24}{r}^{\mathrm{4}} −\mathrm{6}.\mathrm{4}{r}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${r}=\pm\mathrm{2}.\mathrm{24},\pm\mathrm{0}.\mathrm{45} \\ $$$${r}=\mathrm{2}.\mathrm{24}\Rightarrow{cost}=\frac{\mathrm{12}\left(\mathrm{2}.\mathrm{24}\right)^{\mathrm{2}} }{\mathrm{5}×\left(\pm\mathrm{2}.\mathrm{24}\right)\left(\mathrm{2}.\mathrm{24}^{\mathrm{2}} +\mathrm{1}\right)}=\pm\mathrm{0}.\mathrm{89} \\ $$$$\Rightarrow{t}=\mathrm{27}.\mathrm{13}^{\bullet} ,\mathrm{152}.\mathrm{87}^{\bullet} \Rightarrow\begin{cases}{{x}=\mathrm{2}.\mathrm{24}×\left(\pm\mathrm{0}.\mathrm{89}\right)#\pm\mathrm{2}.\mathrm{0}}\\{{y}=\mathrm{2}.\mathrm{24}×\mathrm{0}.\mathrm{46}#\mathrm{1}.\mathrm{0}}\end{cases} \\ $$$${r}=\mathrm{0}.\mathrm{45}\Rightarrow{cost}=\frac{\mathrm{12}\left(.\mathrm{45}\right)^{\mathrm{2}} }{\mathrm{5}×\left(\pm.\mathrm{45}\right)\left(.\mathrm{45}^{\mathrm{2}} +\mathrm{1}\right)}=\pm\mathrm{0}.\mathrm{9} \\ $$$${t}=\mathrm{25}.\mathrm{84}^{\bullet} ,\mathrm{154}.\mathrm{16}^{\bullet} \Rightarrow\begin{cases}{{x}=\mathrm{0}.\mathrm{45}×\left(\pm\mathrm{0}.\mathrm{9}\right)=\pm\mathrm{0}.\mathrm{4}}\\{{y}=\mathrm{0}.\mathrm{45}×\mathrm{0}.\mathrm{45}=\mathrm{0}.\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\left({x},{y}\right)=\left(\pm\mathrm{2},\mathrm{1}\right),\left(\pm\mathrm{0}.\mathrm{4},\mathrm{0}.\mathrm{2}\right)\:.\blacksquare \\ $$

Commented by Tawa1 last updated on 05/Nov/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com