Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 46919 by behi83417@gmail.com last updated on 02/Nov/18

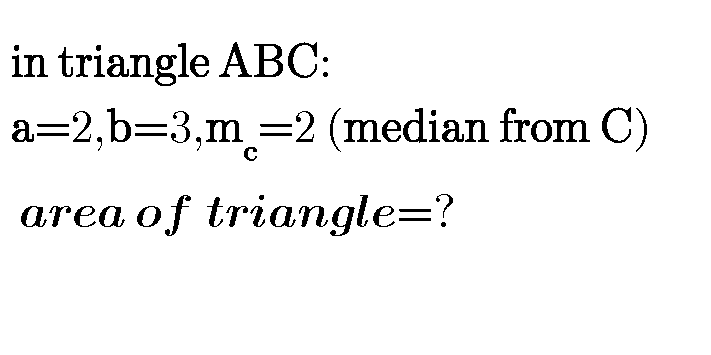
Commented by ajfour last updated on 02/Nov/18

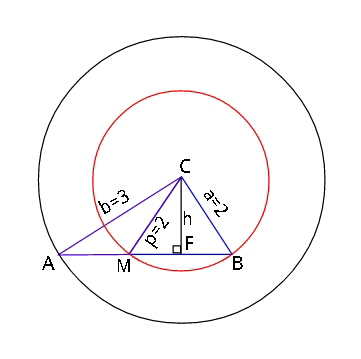
Commented by ajfour last updated on 02/Nov/18

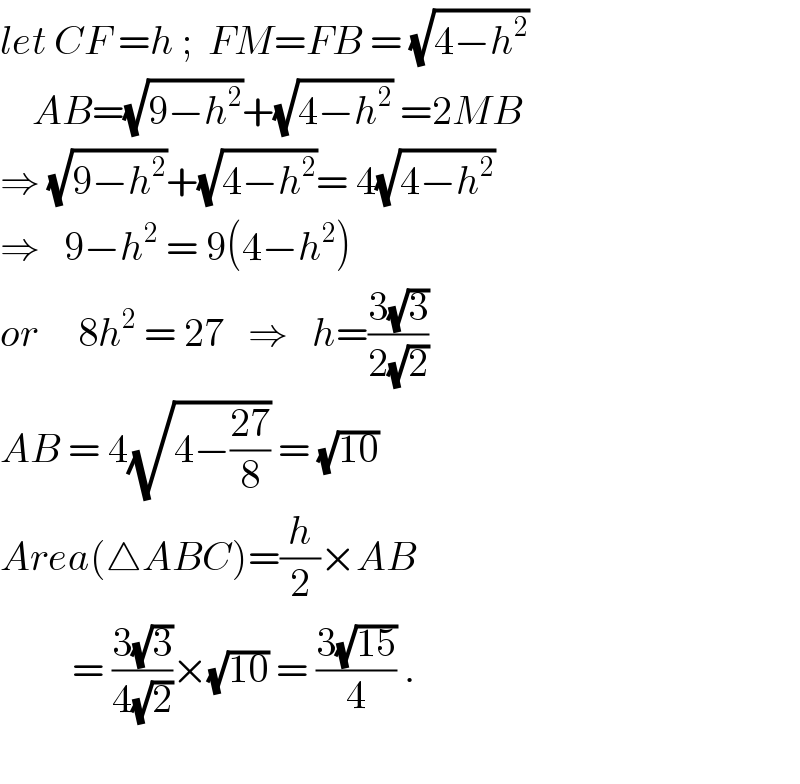
let CF =h ; FM=FB = (√(4−h^2 )) AB=(√(9−h^2 ))+(√(4−h^2 )) =2MB ⇒ (√(9−h^2 ))+(√(4−h^2 ))= 4(√(4−h^2 )) ⇒ 9−h^2 = 9(4−h^2 ) or 8h^2 = 27 ⇒ h=((3(√3))/(2(√2))) AB = 4(√(4−((27)/8))) = (√(10)) Area(△ABC)=(h/2)×AB = ((3(√3))/(4(√2)))×(√(10)) = ((3(√(15)))/4) .

$${let}\:{CF}\:={h}\:;\:\:{FM}={FB}\:=\:\sqrt{\mathrm{4}−{h}^{\mathrm{2}} } \\ $$$$\:\:\:\:{AB}=\sqrt{\mathrm{9}−{h}^{\mathrm{2}} }+\sqrt{\mathrm{4}−{h}^{\mathrm{2}} }\:=\mathrm{2}{MB} \\ $$$$\Rightarrow\:\sqrt{\mathrm{9}−{h}^{\mathrm{2}} }+\sqrt{\mathrm{4}−{h}^{\mathrm{2}} }=\:\mathrm{4}\sqrt{\mathrm{4}−{h}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\mathrm{9}−{h}^{\mathrm{2}} \:=\:\mathrm{9}\left(\mathrm{4}−{h}^{\mathrm{2}} \right) \\ $$$${or}\:\:\:\:\:\mathrm{8}{h}^{\mathrm{2}} \:=\:\mathrm{27}\:\:\:\Rightarrow\:\:\:{h}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{2}}}\: \\ $$$${AB}\:=\:\mathrm{4}\sqrt{\mathrm{4}−\frac{\mathrm{27}}{\mathrm{8}}}\:=\:\sqrt{\mathrm{10}}\: \\ $$$${Area}\left(\bigtriangleup{ABC}\right)=\frac{{h}}{\mathrm{2}}×{AB} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}\sqrt{\mathrm{2}}}×\sqrt{\mathrm{10}}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{15}}}{\mathrm{4}}\:. \\ $$$$ \\ $$

Commented by behi83417@gmail.com last updated on 02/Nov/18

thank you so much sir Ajfour. your answer is right with 13 % defference. area=2.76 units. please also attemp Q#46906.

$${thank}\:{you}\:{so}\:{much}\:{sir}\:{Ajfour}. \\ $$$${your}\:{answer}\:{is}\:{right}\:{with}\:\mathrm{13}\:\% \\ $$$${defference}. \\ $$$${area}=\mathrm{2}.\mathrm{76}\:{units}. \\ $$$${please}\:{also}\:{attemp}\:{Q}#\mathrm{46906}. \\ $$

Commented by ajfour last updated on 02/Nov/18

Behi Sir, i checked, but couldn′t find mistake in my solution..!

$${Behi}\:{Sir},\:{i}\:{checked},\:{but}\:{couldn}'{t} \\ $$$${find}\:{mistake}\:{in}\:{my}\:{solution}..! \\ $$

Commented by MJS last updated on 02/Nov/18

AM=2m MF=FB=m m^2 +h^2 =4 9m^2 +h^2 =9 ⇒ m=((√(10))/4)∧h=((3(√6))/4) ⇒ c=AB=4m=(√(10)) ⇒ area=((3(√(15)))/4) ...so Sir Aifour is right

$${AM}=\mathrm{2m} \\ $$$${MF}={FB}=\mathrm{m} \\ $$$${m}^{\mathrm{2}} +{h}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{9}{m}^{\mathrm{2}} +{h}^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow\:{m}=\frac{\sqrt{\mathrm{10}}}{\mathrm{4}}\wedge{h}=\frac{\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{4}} \\ $$$$\Rightarrow\:{c}={AB}=\mathrm{4}{m}=\sqrt{\mathrm{10}} \\ $$$$\Rightarrow\:\mathrm{area}=\frac{\mathrm{3}\sqrt{\mathrm{15}}}{\mathrm{4}} \\ $$$$...\mathrm{so}\:\mathrm{Sir}\:\mathrm{Aifour}\:\mathrm{is}\:\mathrm{right} \\ $$

Commented by behi83417@gmail.com last updated on 02/Nov/18

thank you very much sir. you and sir Ajfour,use : [a=2,m=2]to take CM^△ B,as isoscale triangle.now if a≠2 ,what can we do? [say a=5,for example] (for:a=5,b=3,m=2, area=((8(√(161)))/(15))=6.77)

$${thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$$${you}\:{and}\:{sir}\:{Ajfour},{use}\:: \\ $$$$\left[{a}=\mathrm{2},{m}=\mathrm{2}\right]{to}\:{take}\:{C}\overset{\bigtriangleup} {{M}B},{as}\:{isoscale} \\ $$$${triangle}.{now}\:{if}\:{a}\neq\mathrm{2}\:,{what}\:{can} \\ $$$${we}\:{do}?\:\left[{say}\:{a}=\mathrm{5},{for}\:{example}\right] \\ $$$$\left({for}:{a}=\mathrm{5},{b}=\mathrm{3},{m}=\mathrm{2},\right. \\ $$$$\left.{area}=\frac{\mathrm{8}\sqrt{\mathrm{161}}}{\mathrm{15}}=\mathrm{6}.\mathrm{77}\right) \\ $$

Commented by behi83417@gmail.com last updated on 03/Nov/18

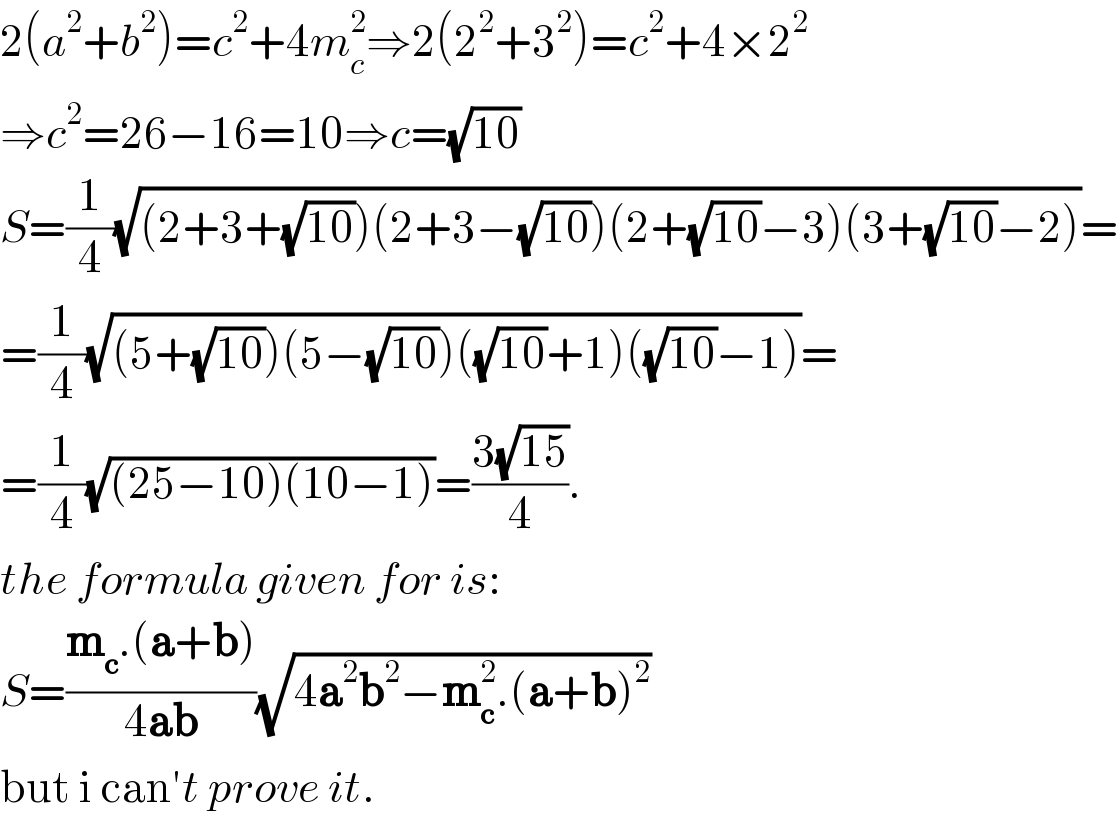
2(a^2 +b^2 )=c^2 +4m_c ^2 ⇒2(2^2 +3^2 )=c^2 +4×2^2 ⇒c^2 =26−16=10⇒c=(√(10)) S=(1/4)(√((2+3+(√(10)))(2+3−(√(10)))(2+(√(10))−3)(3+(√(10))−2)))= =(1/4)(√((5+(√(10)))(5−(√(10)))((√(10))+1)((√(10))−1)))= =(1/4)(√((25−10)(10−1)))=((3(√(15)))/4). the formula given for is: S=((m_c .(a+b))/(4ab))(√(4a^2 b^2 −m_c ^2 .(a+b)^2 )) but i can′t prove it.

$$\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)={c}^{\mathrm{2}} +\mathrm{4}{m}_{{c}} ^{\mathrm{2}} \Rightarrow\mathrm{2}\left(\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right)={c}^{\mathrm{2}} +\mathrm{4}×\mathrm{2}^{\mathrm{2}} \\ $$$$\Rightarrow{c}^{\mathrm{2}} =\mathrm{26}−\mathrm{16}=\mathrm{10}\Rightarrow{c}=\sqrt{\mathrm{10}} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left(\mathrm{2}+\mathrm{3}+\sqrt{\mathrm{10}}\right)\left(\mathrm{2}+\mathrm{3}−\sqrt{\mathrm{10}}\right)\left(\mathrm{2}+\sqrt{\mathrm{10}}−\mathrm{3}\right)\left(\mathrm{3}+\sqrt{\mathrm{10}}−\mathrm{2}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left(\mathrm{5}+\sqrt{\mathrm{10}}\right)\left(\mathrm{5}−\sqrt{\mathrm{10}}\right)\left(\sqrt{\mathrm{10}}+\mathrm{1}\right)\left(\sqrt{\mathrm{10}}−\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left(\mathrm{25}−\mathrm{10}\right)\left(\mathrm{10}−\mathrm{1}\right)}=\frac{\mathrm{3}\sqrt{\mathrm{15}}}{\mathrm{4}}. \\ $$$${the}\:{formula}\:{given}\:{for}\:{is}: \\ $$$${S}=\frac{\boldsymbol{\mathrm{m}}_{\boldsymbol{\mathrm{c}}} .\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\right)}{\mathrm{4}\boldsymbol{\mathrm{ab}}}\sqrt{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{m}}_{\boldsymbol{\mathrm{c}}} ^{\mathrm{2}} .\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{but}\:\mathrm{i}\:\mathrm{can}'{t}\:{prove}\:{it}. \\ $$

Commented by ajfour last updated on 03/Nov/18

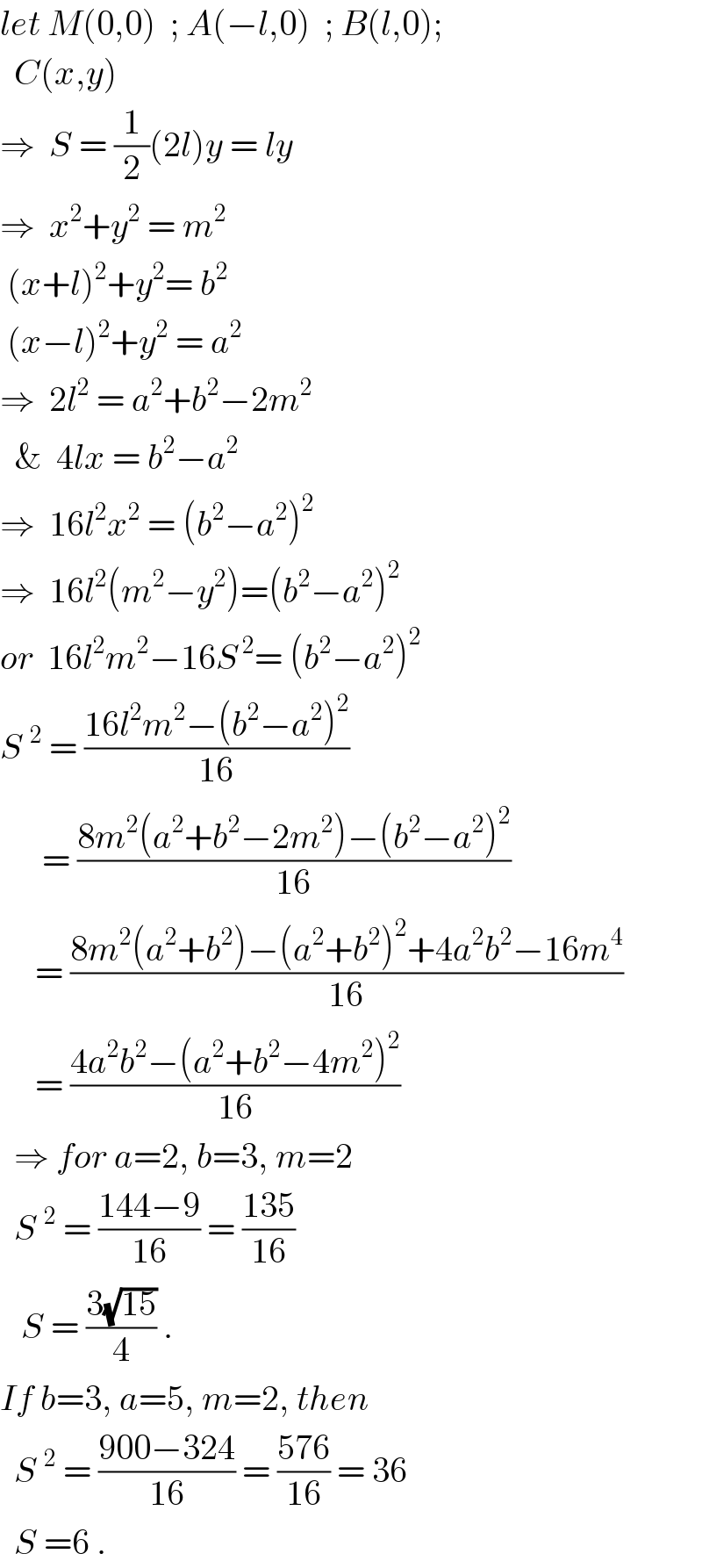
let M(0,0) ; A(−l,0) ; B(l,0); C(x,y) ⇒ S = (1/2)(2l)y = ly ⇒ x^2 +y^2 = m^2 (x+l)^2 +y^2 = b^2 (x−l)^2 +y^2 = a^2 ⇒ 2l^2 = a^2 +b^2 −2m^2 & 4lx = b^2 −a^2 ⇒ 16l^2 x^2 = (b^2 −a^2 )^2 ⇒ 16l^2 (m^2 −y^2 )=(b^2 −a^2 )^2 or 16l^2 m^2 −16S^( 2) = (b^2 −a^2 )^2 S^2 = ((16l^2 m^2 −(b^2 −a^2 )^2 )/(16)) = ((8m^2 (a^2 +b^2 −2m^2 )−(b^2 −a^2 )^2 )/(16)) = ((8m^2 (a^2 +b^2 )−(a^2 +b^2 )^2 +4a^2 b^2 −16m^4 )/(16)) = ((4a^2 b^2 −(a^2 +b^2 −4m^2 )^2 )/(16)) ⇒ for a=2, b=3, m=2 S^2 = ((144−9)/(16)) = ((135)/(16)) S = ((3(√(15)))/4) . If b=3, a=5, m=2, then S^2 = ((900−324)/(16)) = ((576)/(16)) = 36 S =6 .

$${let}\:{M}\left(\mathrm{0},\mathrm{0}\right)\:\:;\:{A}\left(−{l},\mathrm{0}\right)\:\:;\:{B}\left({l},\mathrm{0}\right); \\ $$$$\:\:{C}\left({x},{y}\right)\:\:\: \\ $$$$\Rightarrow\:\:{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{l}\right){y}\:=\:{ly} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:{m}^{\mathrm{2}} \\ $$$$\:\left({x}+{l}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\:{b}^{\mathrm{2}} \\ $$$$\:\left({x}−{l}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}{l}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{m}^{\mathrm{2}} \\ $$$$\:\:\&\:\:\mathrm{4}{lx}\:=\:{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{16}{l}^{\mathrm{2}} {x}^{\mathrm{2}} \:=\:\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{16}{l}^{\mathrm{2}} \left({m}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)=\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${or}\:\:\mathrm{16}{l}^{\mathrm{2}} {m}^{\mathrm{2}} −\mathrm{16}{S}^{\:\mathrm{2}} =\:\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${S}\:^{\mathrm{2}} \:=\:\frac{\mathrm{16}{l}^{\mathrm{2}} {m}^{\mathrm{2}} −\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{8}{m}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{m}^{\mathrm{2}} \right)−\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{8}{m}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{16}{m}^{\mathrm{4}} }{\mathrm{16}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{4}{m}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\:\:\Rightarrow\:{for}\:{a}=\mathrm{2},\:{b}=\mathrm{3},\:{m}=\mathrm{2} \\ $$$$\:\:{S}\:^{\mathrm{2}} \:=\:\frac{\mathrm{144}−\mathrm{9}}{\mathrm{16}}\:=\:\frac{\mathrm{135}}{\mathrm{16}} \\ $$$$\:\:\:{S}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{15}}}{\mathrm{4}}\:. \\ $$$${If}\:{b}=\mathrm{3},\:{a}=\mathrm{5},\:{m}=\mathrm{2},\:{then} \\ $$$$\:\:{S}\:^{\mathrm{2}} \:=\:\frac{\mathrm{900}−\mathrm{324}}{\mathrm{16}}\:=\:\frac{\mathrm{576}}{\mathrm{16}}\:=\:\mathrm{36} \\ $$$$\:\:{S}\:=\mathrm{6}\:. \\ $$

Commented by behi83417@gmail.com last updated on 03/Nov/18

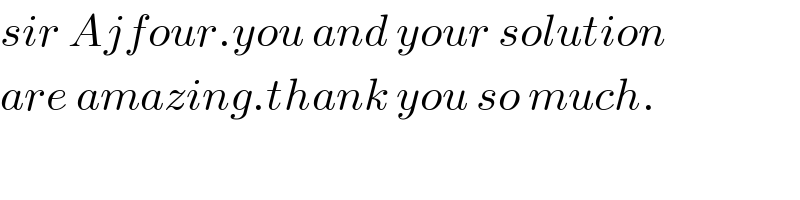
sir Ajfour.you and your solution are amazing.thank you so much.

$${sir}\:{Ajfour}.{you}\:{and}\:{your}\:{solution} \\ $$$${are}\:{amazing}.{thank}\:{you}\:{so}\:{much}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com