
Question Number 46889 by ajfour last updated on 02/Nov/18
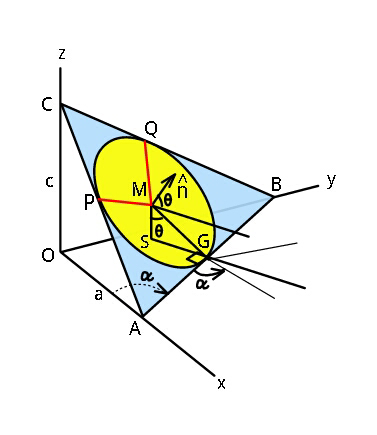
Commented by ajfour last updated on 02/Nov/18
$${Q}.\mathrm{46611}\:\left({Alternate}\:{approach}\right) \\ $$
Answered by ajfour last updated on 02/Nov/18
![n^� = cos θ(sin αi^� +cos αj^� )+sin θk^� r_M ^� =(hi^� +kj^� )−Rsin θ(sin αi^� +cos αj^� ) +Rcos θk^� asin α = d bcos α = d ctan θ = d y_P = 0 & [((n^� ×(ck^� −ai^� ))/(√(c^2 +a^2 )))]_y = (r_P ^� −r_M ^� )_y ⇒ −R[((ccos θsin α+asin θ)/(√(a^2 +c^2 )))] = −k+Rsin θcos α ...(i) x_Q =0 & [(((ck^� −bj^� )×n^� )/(√(b^2 +c^2 )))]_x =(r_Q ^� −r_M ^� )_x ⇒ −R[((ccos θcos α+bsin θ)/(√(b^2 +c^2 )))] = −h+Rsin θsin α ....(ii) From (i)&(ii), we shall obtain α and θ ; using asin α = d bcos α = d ctan θ = d , in eqs. (i) & (ii) ((R[((cos^2 θ)/(sin θ))sin α+((sin θ)/(sin α))])/(√((1/(sin^2 α))+((cos^2 θ)/(sin^2 θ)))))=k−Rsin θcos α similarly ((R[((cos^2 θ)/(sin θ))cos α+((sin θ)/(cos α))])/(√((1/(cos^2 α))+((cos^2 θ)/(sin^2 θ)))))=h−Rsin θsin α ________________________ rearranging gives R(√(sin^2 θ+sin^2 αcos^2 θ)) = k−Rsin θcos α ...(A) R(√(sin^2 θ+cos^2 θcos^2 α)) = h−Rsin θsin α ....(B) ________________________ squaring and adding (A)&(B) 2R^2 sin^2 θ+R^2 cos^2 θ = h^2 +k^2 + R^2 sin^2 θ−2Rsin θ(hsin α+kcos α) ⇒ 2Rsin θ=((h^2 +k^2 −R^2 )/(hsin α+kcos α)) ..(I) Changing (A) to R^2 sin^2 θcos^2 α+R^2 sin^2 α = (k−Rsin θcos α)^2 Now let Rsin θcos α = t ⇒ t^2 +R^2 sin^2 α=k^2 +t^2 −2kt ⇒ 2t=((k^2 −R^2 sin^2 α)/k) Now using (I): ⇒ 2Rsin θ = (k/(cos α))−((R^2 sin^2 α)/(kcos α)) ⇒ ((h^2 +k^2 −R^2 )/(hsin α+kcos α))=((k^2 −R^2 sin^2 α)/(kcos α)) ⇒ ((h^2 −R^2 cos^2 α)/(hsin α)) = ((k^2 −R^2 sin^2 α)/(kcos α)) ________________________ let m=tan α ⇒ ((h^2 (1+m^2 )−R^2 )/(k^2 (1+m^2 )−R^2 m^2 )) = ((mh)/k) this eq. provides for 𝛂 ; and then from (I): θ=sin^(−1) [((h^2 +k^2 −R^2 )/(2R(hsin α+kcos α)))] ________________________.](Q46895.png)
$$\hat {{n}}\:=\:\mathrm{cos}\:\theta\left(\mathrm{sin}\:\alpha\hat {{i}}+\mathrm{cos}\:\alpha\hat {{j}}\right)+\mathrm{sin}\:\theta\hat {{k}} \\ $$$$\bar {{r}}_{{M}} =\left({h}\hat {{i}}+{k}\hat {{j}}\right)−{R}\mathrm{sin}\:\theta\left(\mathrm{sin}\:\alpha\hat {{i}}+\mathrm{cos}\:\alpha\hat {{j}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{R}\mathrm{cos}\:\theta\hat {{k}} \\ $$$${a}\mathrm{sin}\:\alpha\:=\:{d} \\ $$$${b}\mathrm{cos}\:\alpha\:=\:{d} \\ $$$${c}\mathrm{tan}\:\theta\:=\:{d} \\ $$$$\:\:\:{y}_{{P}} =\:\mathrm{0}\: \\ $$$$\&\:\:\left[\frac{\hat {{n}}×\left({c}\hat {{k}}−{a}\hat {{i}}\right)}{\sqrt{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} }}\right]_{{y}} =\:\left(\bar {{r}}_{{P}} −\bar {{r}}_{{M}} \right)_{{y}} \\ $$$$\Rightarrow\:\:−{R}\left[\frac{{c}\mathrm{cos}\:\theta\mathrm{sin}\:\alpha+{a}\mathrm{sin}\:\theta}{\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−{k}+{R}\mathrm{sin}\:\theta\mathrm{cos}\:\alpha\:\:\:...\left({i}\right) \\ $$$$\:\:\:{x}_{{Q}} =\mathrm{0}\:\:\& \\ $$$$\:\:\:\left[\frac{\left({c}\hat {{k}}−{b}\hat {{j}}\right)×\hat {{n}}}{\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }}\right]_{{x}} =\left(\bar {{r}}_{{Q}} −\bar {{r}}_{{M}} \right)_{{x}} \\ $$$$\Rightarrow\:−{R}\left[\frac{{c}\mathrm{cos}\:\theta\mathrm{cos}\:\alpha+{b}\mathrm{sin}\:\theta}{\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:−{h}+{R}\mathrm{sin}\:\theta\mathrm{sin}\:\alpha\:\:\:\:....\left({ii}\right) \\ $$$$\:\:{From}\:\left({i}\right)\&\left({ii}\right),\:{we}\:{shall}\:{obtain} \\ $$$$\:\:\alpha\:{and}\:\theta\:;\:\:{using} \\ $$$${a}\mathrm{sin}\:\alpha\:=\:{d} \\ $$$${b}\mathrm{cos}\:\alpha\:=\:{d} \\ $$$${c}\mathrm{tan}\:\theta\:=\:{d}\:\:\:\:,\:{in}\:{eqs}.\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:\frac{{R}\left[\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:\theta}\mathrm{sin}\:\alpha+\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:\alpha}\right]}{\sqrt{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \alpha}+\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:^{\mathrm{2}} \theta}}}={k}−{R}\mathrm{sin}\:\theta\mathrm{cos}\:\alpha \\ $$$${similarly} \\ $$$$\frac{{R}\left[\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:\theta}\mathrm{cos}\:\alpha+\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\alpha}\right]}{\sqrt{\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \alpha}+\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:^{\mathrm{2}} \theta}}}={h}−{R}\mathrm{sin}\:\theta\mathrm{sin}\:\alpha \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${rearranging}\:{gives} \\ $$$${R}\sqrt{\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{sin}\:^{\mathrm{2}} \alpha\mathrm{cos}\:^{\mathrm{2}} \theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{k}−{R}\mathrm{sin}\:\theta\mathrm{cos}\:\alpha\:\:\:\:...\left({A}\right) \\ $$$${R}\sqrt{\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \alpha} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:{h}−{R}\mathrm{sin}\:\theta\mathrm{sin}\:\alpha\:\:\:\:....\left({B}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:{squaring}\:{and}\:{adding}\:\left({A}\right)\&\left({B}\right) \\ $$$$\:\:\:\mathrm{2}{R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\:=\:{h}^{\mathrm{2}} +{k}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:{R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta−\mathrm{2}{R}\mathrm{sin}\:\theta\left({h}\mathrm{sin}\:\alpha+{k}\mathrm{cos}\:\alpha\right) \\ $$$$\Rightarrow\:\mathrm{2}{R}\mathrm{sin}\:\theta=\frac{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} }{{h}\mathrm{sin}\:\alpha+{k}\mathrm{cos}\:\alpha}\:\:..\left({I}\right) \\ $$$${Changing}\:\left({A}\right)\:{to} \\ $$$${R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \alpha+{R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({k}−{R}\mathrm{sin}\:\theta\mathrm{cos}\:\alpha\right)^{\mathrm{2}} \\ $$$${Now}\:{let}\:\:\:{R}\mathrm{sin}\:\theta\mathrm{cos}\:\alpha\:=\:{t} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{2}} +{R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha={k}^{\mathrm{2}} +{t}^{\mathrm{2}} −\mathrm{2}{kt} \\ $$$$\Rightarrow\:\mathrm{2}{t}=\frac{{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}{{k}} \\ $$$${Now}\:{using}\:\left({I}\right): \\ $$$$\Rightarrow\:\mathrm{2}{R}\mathrm{sin}\:\theta\:=\:\frac{{k}}{\mathrm{cos}\:\alpha}−\frac{{R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}{{k}\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow\:\frac{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} }{{h}\mathrm{sin}\:\alpha+{k}\mathrm{cos}\:\alpha}=\frac{{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}{{k}\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow\:\frac{{h}^{\mathrm{2}} −{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha}{{h}\mathrm{sin}\:\alpha}\:=\:\frac{{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}{{k}\mathrm{cos}\:\alpha} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${let}\:\:{m}=\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\:\frac{{h}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)−{R}^{\mathrm{2}} }{{k}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)−{R}^{\mathrm{2}} {m}^{\mathrm{2}} }\:=\:\frac{{mh}}{{k}} \\ $$$${this}\:{eq}.\:{provides}\:{for}\:\boldsymbol{\alpha}\:;\:{and}\:{then} \\ $$$${from}\:\left({I}\right): \\ $$$$\:\:\:\:\:\theta=\mathrm{sin}^{−\mathrm{1}} \left[\frac{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} }{\mathrm{2}{R}\left({h}\mathrm{sin}\:\alpha+{k}\mathrm{cos}\:\alpha\right)}\right]\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$
Commented by ajfour last updated on 02/Nov/18

$${In}\:{excellent}\:{agreement}\:{with} \\ $$$${your}\:{result}\:{Sir},\:{coz}\:{they}\:{are}\:{same}. \\ $$
Commented by MrW3 last updated on 02/Nov/18

$${yes},\:{sir}. \\ $$$${it}'{s}\:{a}\:{marvellous}\:{job}\:{what}\:{you}\:{did}! \\ $$$${really}\:{nice}\:{method}! \\ $$
Commented by MrW3 last updated on 02/Nov/18

$${You}\:{can}\:{remeber}\:{that}\:{I}\:{was}\:{unsure}\:{if} \\ $$$${the}\:{position}\:{of}\:{the}\:{ring}\:{is}\:{unique}.\:{Now} \\ $$$${I}\:{know}\:{the}\:{position}\:{of}\:{the}\:{ring}\:{is} \\ $$$${unique}\:{with}\:{the}\:{given}\:{point}\:{G}.\:{But} \\ $$$${with}\:{some}\:{values}\:{of}\:{R}\:{there}\:{can}\:{be} \\ $$$${two}\:{or}\:{three}\:{possible}\:{positions}\:{for} \\ $$$${the}\:{ring}. \\ $$
Commented by ajfour last updated on 02/Nov/18

$${yes}\:{sir},\:{thank}\:{you}\:{for}\:{solving}\:{it} \\ $$$${by}\:{two}\:{methods};\:{but}\:{i}\:{could} \\ $$$${have}\:{guessed}\:{wrongly}\:\:{at}\:{least} \\ $$$$\:{two}\:{roots}\:{for}\:\alpha\:{as}\:{complex}.. \\ $$$${every}\:{time}. \\ $$
Commented by MrW3 last updated on 02/Nov/18

$${there}\:{could}\:{be}\:{three}\:{positive}\:{roots}\:{or} \\ $$$${one}\:{positive}\:{and}\:{two}\:{negative}\:{or}\:{two} \\ $$$${positive}\:{and}\:{one}\:{negative}\:{roots}.\:{that} \\ $$$${means}\:{we}\:{can}\:{get}:\:{one}\:{position},\:{two} \\ $$$${positions}\:{or}\:{three}\:{positions}\:{for}\:{the} \\ $$$${ring}. \\ $$
Commented by peter frank last updated on 02/Nov/18

$$\mathrm{pls}\:\mathrm{help}\:\mathrm{Q}\:\mathrm{46838},\mathrm{46829} \\ $$
