Question Number 46546 by ajfour last updated on 28/Oct/18
Commented by ajfour last updated on 28/Oct/18

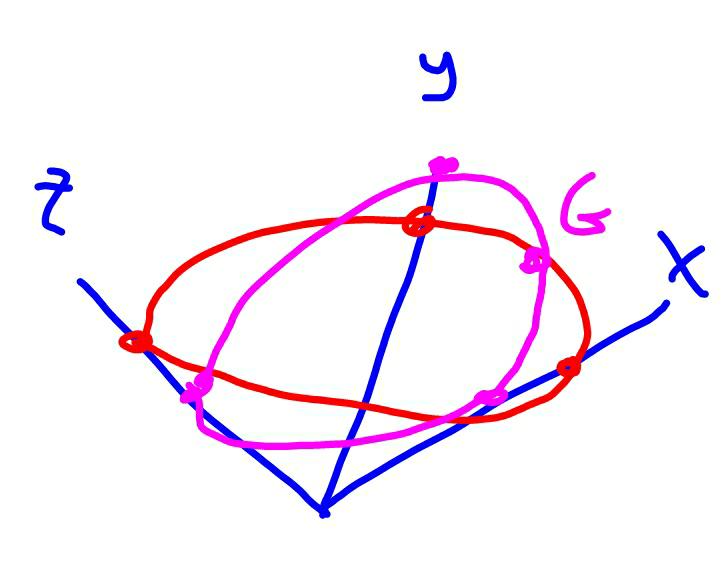
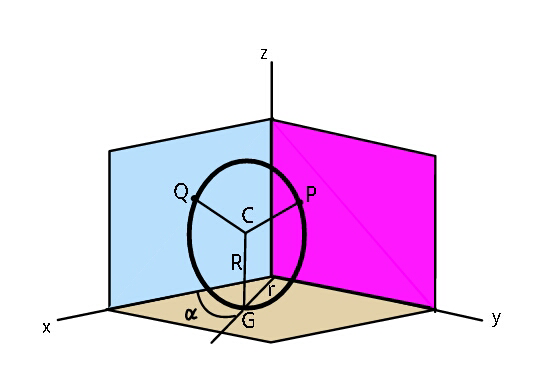
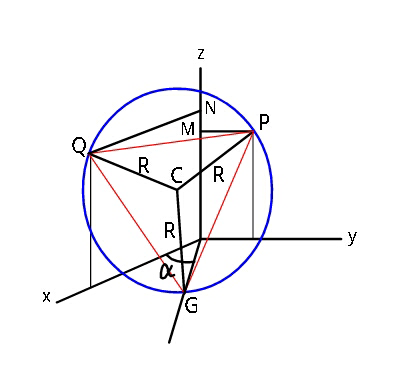
$${A}\:{circular}\:{ring}\:{of}\:{radius}\:{R},\:{rests} \\ $$$${against}\:{two}\:{adjacent}\:{walls}\:{and} \\ $$$${ground}.\:{If}\:{G}\left({r}\mathrm{cos}\:\alpha,\:{r}\mathrm{sin}\:\alpha,\:\mathrm{0}\right), \\ $$$${find}\:{coordinates}\:{of}\:{P}\:{and}\:{Q} \\ $$$$\left({points}\:{of}\:{contact}\:{of}\:{ring}\:{with}\right. \\ $$$$\left.{the}\:{walls}\right). \\ $$
Commented by ajfour last updated on 28/Oct/18
Commented by MrW3 last updated on 28/Oct/18
Commented by MrW3 last updated on 28/Oct/18
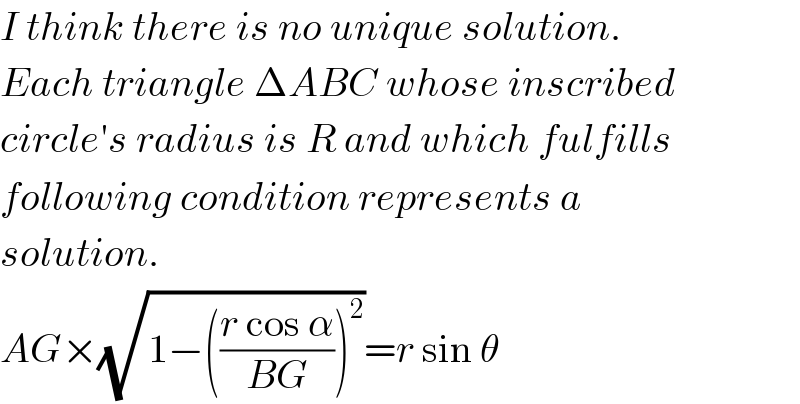
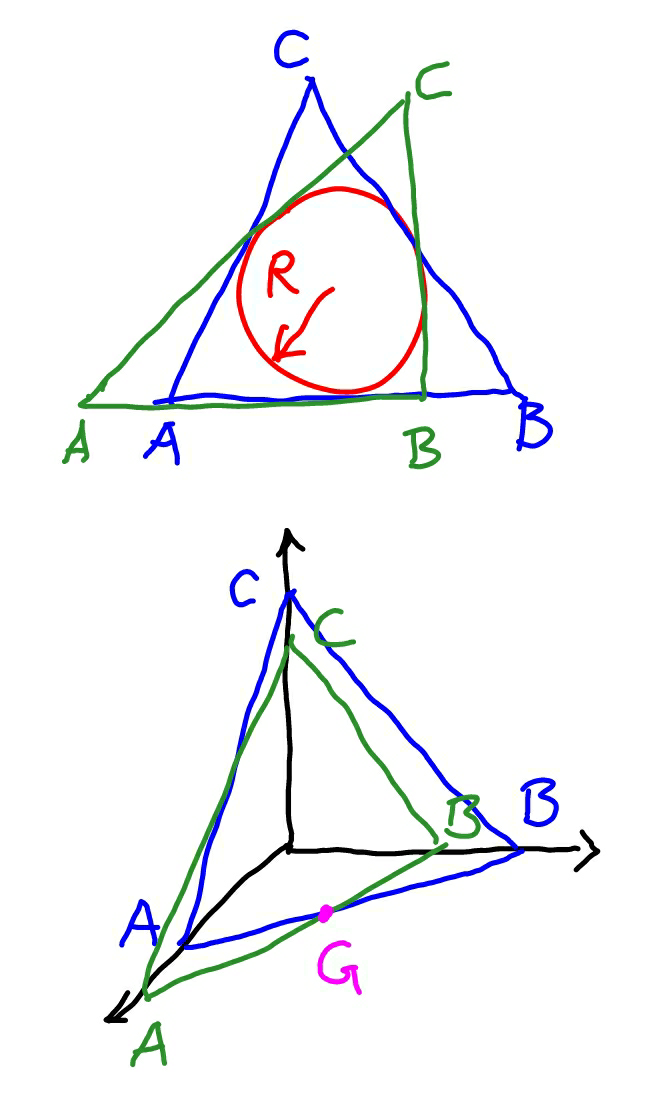
$${I}\:{think}\:{there}\:{is}\:{no}\:{unique}\:{solution}. \\ $$$${Each}\:{triangle}\:\Delta{ABC}\:{whose}\:{inscribed} \\ $$$${circle}'{s}\:{radius}\:{is}\:{R}\:{and}\:{which}\:{fulfills} \\ $$$${following}\:{condition}\:{represents}\:{a} \\ $$$${solution}. \\ $$$${AG}×\sqrt{\mathrm{1}−\left(\frac{{r}\:\mathrm{cos}\:\alpha}{{BG}}\right)^{\mathrm{2}} }={r}\:\mathrm{sin}\:\theta \\ $$
Commented by ajfour last updated on 29/Oct/18

$${But}\:{i}\:{intuitively}\:{feel}\:{it}\:{locked} \\ $$$${if}\:{G}\:\:{and}\:{radius}\:{R}\:{given}\:{and} \\ $$$${that}\:{it}\:\left({ring}\right)\:{rests}\:{against}\:{both} \\ $$$${walls},\:{Sir}. \\ $$
Commented by MrW3 last updated on 29/Oct/18
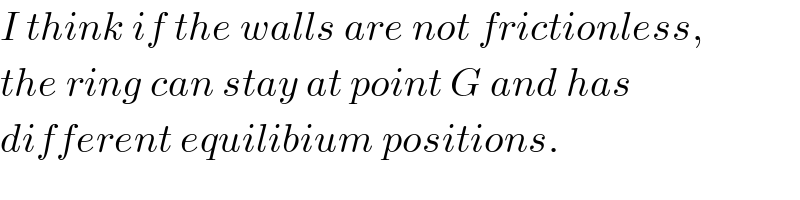
$${I}\:{think}\:{if}\:{the}\:{walls}\:{are}\:{not}\:{frictionless}, \\ $$$${the}\:{ring}\:{can}\:{stay}\:{at}\:{point}\:{G}\:{and}\:{has} \\ $$$${different}\:{equilibium}\:{positions}. \\ $$
Commented by MrW3 last updated on 29/Oct/18