Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 46414 by Meritguide1234 last updated on 25/Oct/18

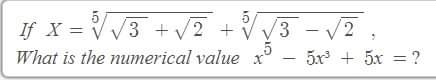
Commented by math1967 last updated on 25/Oct/18

Is the answar 2(√3)

$${Is}\:{the}\:{answar}\:\mathrm{2}\sqrt{\mathrm{3}} \\ $$

Answered by math1967 last updated on 25/Oct/18

let (√3) +(√2) =a ∴(√3) −(√2) =(1/a) ∴x= ^5 (√(a )) +(1/(a)^(1/5) )=p+(1/p) [let ^5 (√a) =p] x^3 =p^3 +(1/p^3 ) +3(p+(1/p)) x^3 −3x=p^3 +(1/p^3 ) [∵p+(1/p)=x] now x^5 =p^5 +(1/p^5 ) +5(p^3 +(1/p^3 ))+10(p+(1/p)) x^5 =p^5 +(1/p^5 ) +5(x^3 −3x)+10x x^5 −5x^3 +5x= (√3) +(√2) +(1/((√3) −(√2))) ∴ x^3 −5x^3 +5x=(√3) +(√2) +(√3) −(√2)=2(√3)

$${let}\:\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{2}}\:={a}\:\therefore\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{2}}\:=\frac{\mathrm{1}}{{a}} \\ $$$$\therefore{x}=\overset{\mathrm{5}} {\:}\sqrt{{a}\:}\:+\frac{\mathrm{1}}{\sqrt[{\mathrm{5}}]{{a}}}={p}+\frac{\mathrm{1}}{{p}}\:\:\left[{let}\overset{\mathrm{5}} {\:}\sqrt{{a}}\:={p}\right] \\ $$$$\:\:{x}^{\mathrm{3}} ={p}^{\mathrm{3}} +\frac{\mathrm{1}}{{p}^{\mathrm{3}} }\:+\mathrm{3}\left({p}+\frac{\mathrm{1}}{{p}}\right) \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}={p}^{\mathrm{3}} +\frac{\mathrm{1}}{{p}^{\mathrm{3}} }\:\:\:\:\left[\because{p}+\frac{\mathrm{1}}{{p}}={x}\right] \\ $$$${now}\:{x}^{\mathrm{5}} ={p}^{\mathrm{5}} +\frac{\mathrm{1}}{{p}^{\mathrm{5}} }\:+\mathrm{5}\left({p}^{\mathrm{3}} +\frac{\mathrm{1}}{{p}^{\mathrm{3}} }\right)+\mathrm{10}\left({p}+\frac{\mathrm{1}}{{p}}\right) \\ $$$${x}^{\mathrm{5}} ={p}^{\mathrm{5}} +\frac{\mathrm{1}}{{p}^{\mathrm{5}} }\:+\mathrm{5}\left({x}^{\mathrm{3}} −\mathrm{3}{x}\right)+\mathrm{10}{x} \\ $$$${x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{3}} +\mathrm{5}{x}=\:\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{2}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{2}}} \\ $$$$\therefore\:{x}^{\mathrm{3}} −\mathrm{5}{x}^{\mathrm{3}} +\mathrm{5}{x}=\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$

Commented by Meritguide1234 last updated on 26/Oct/18

nice solution

$${nice}\:{solution} \\ $$

Commented by math1967 last updated on 26/Oct/18

Thank you sir

$${Thank}\:{you}\:{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 25/Oct/18

x=a^(1/5) +a^(−(1/5)) x^5 −5x^3 +5x (a^(1/5) +a^((−1)/5) )^5 −5(a^(1/5) +a^((−1)/5) )^3 +5(a^(1/5) +a^((−1)/5) ) =a+5c_1 a^(4/5) a^((−1)/5) +5c_2 a^(3/5) a^((−2)/5) +5c_3 a^(2/5) a^((−3)/5) +5c_4 a^(1/5) a^((−4)/5) +5c_5 a^(−1) −5(a^(3/5) +3c_1 a^(2/5) a^((−1)/5) +3c_2 a^(1/5) a^((−2)/5) +a^((−3)/(5))) +5(a^(1/5) +a^((−1)/5) ) =a+5a^(3/5) +10a^(1/5) +10a^((−1)/5) +5a^((−3)/5) +(1/a)+ −5a^(3/5) −15a^(1/5) −15a^((−1)/5) −5a^((−3)/5) +5a^(1/5) +5^((−1)/5) =a+(1/a)=(√3) +(√2) +(√3) −(√2) =2(√3) answer

$${x}={a}^{\frac{\mathrm{1}}{\mathrm{5}}} +{a}^{−\frac{\mathrm{1}}{\mathrm{5}}} \\ $$$${x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{3}} +\mathrm{5}{x} \\ $$$$\left({a}^{\frac{\mathrm{1}}{\mathrm{5}}} +{a}^{\frac{−\mathrm{1}}{\mathrm{5}}} \right)^{\mathrm{5}} −\mathrm{5}\left({a}^{\frac{\mathrm{1}}{\mathrm{5}}} +{a}^{\frac{−\mathrm{1}}{\mathrm{5}}} \right)^{\mathrm{3}} +\mathrm{5}\left({a}^{\frac{\mathrm{1}}{\mathrm{5}}} +{a}^{\frac{−\mathrm{1}}{\mathrm{5}}} \right) \\ $$$$={a}+\mathrm{5}{c}_{\mathrm{1}} {a}^{\frac{\mathrm{4}}{\mathrm{5}}} {a}^{\frac{−\mathrm{1}}{\mathrm{5}}} +\mathrm{5}{c}_{\mathrm{2}} {a}^{\frac{\mathrm{3}}{\mathrm{5}}} {a}^{\frac{−\mathrm{2}}{\mathrm{5}}} +\mathrm{5}{c}_{\mathrm{3}} {a}^{\frac{\mathrm{2}}{\mathrm{5}}} {a}^{\frac{−\mathrm{3}}{\mathrm{5}}} +\mathrm{5}{c}_{\mathrm{4}} {a}^{\frac{\mathrm{1}}{\mathrm{5}}} {a}^{\frac{−\mathrm{4}}{\mathrm{5}}} +\mathrm{5}{c}_{\mathrm{5}} {a}^{−\mathrm{1}} \\ $$$$−\mathrm{5}\left({a}^{\frac{\mathrm{3}}{\mathrm{5}}} +\mathrm{3}{c}_{\mathrm{1}} {a}^{\frac{\mathrm{2}}{\mathrm{5}}} {a}^{\frac{−\mathrm{1}}{\mathrm{5}}} +\mathrm{3}{c}_{\mathrm{2}} {a}^{\frac{\mathrm{1}}{\mathrm{5}}} {a}^{\frac{−\mathrm{2}}{\mathrm{5}}} +{a}^{\frac{−\mathrm{3}}{\left.\mathrm{5}\right)}} \right. \\ $$$$+\mathrm{5}\left({a}^{\frac{\mathrm{1}}{\mathrm{5}}} +{a}^{\frac{−\mathrm{1}}{\mathrm{5}}} \right) \\ $$$$={a}+\mathrm{5}{a}^{\frac{\mathrm{3}}{\mathrm{5}}} +\mathrm{10}{a}^{\frac{\mathrm{1}}{\mathrm{5}}} +\mathrm{10}{a}^{\frac{−\mathrm{1}}{\mathrm{5}}} +\mathrm{5}{a}^{\frac{−\mathrm{3}}{\mathrm{5}}} +\frac{\mathrm{1}}{{a}}+ \\ $$$$\:\:\:−\mathrm{5}{a}^{\frac{\mathrm{3}}{\mathrm{5}}} −\mathrm{15}{a}^{\frac{\mathrm{1}}{\mathrm{5}}} −\mathrm{15}{a}^{\frac{−\mathrm{1}}{\mathrm{5}}} −\mathrm{5}{a}^{\frac{−\mathrm{3}}{\mathrm{5}}} +\mathrm{5}{a}^{\frac{\mathrm{1}}{\mathrm{5}}} +\mathrm{5}^{\frac{−\mathrm{1}}{\mathrm{5}}} \\ $$$$={a}+\frac{\mathrm{1}}{{a}}=\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{2}}\:=\mathrm{2}\sqrt{\mathrm{3}}\:{answer} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Meritguide1234 last updated on 26/Oct/18

very good Mr.Tanmoy Are you professor?

$${very}\:{good}\:{Mr}.{Tanmoy} \\ $$$${Are}\:{you}\:{professor}? \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 26/Oct/18

no sir..i enjoy it...i have interest in physics and mathematics...

$${no}\:{sir}..{i}\:{enjoy}\:\:{it}...{i}\:{have}\:{interest}\:{in}\:{physics} \\ $$$${and}\:{mathematics}... \\ $$

Commented by Meritguide1234 last updated on 26/Oct/18

basically i am teacher of senior secondary school of taiwan.

$${basically}\:{i}\:{am}\:{teacher}\:{of}\:{senior}\:{secondary}\:{school}\:{of}\:{taiwan}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com