
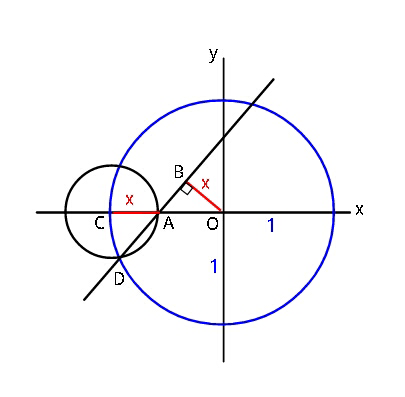
Question Number 46338 by ajfour last updated on 24/Oct/18
Commented by MJS last updated on 24/Oct/18
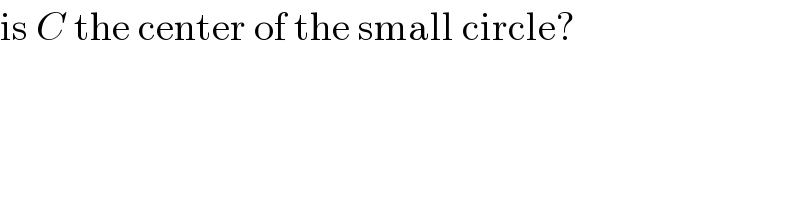
$$\mathrm{is}\:{C}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{small}\:\mathrm{circle}? \\ $$
Commented by ajfour last updated on 24/Oct/18

$${yes}\:{Sir}. \\ $$
Answered by MJS last updated on 24/Oct/18
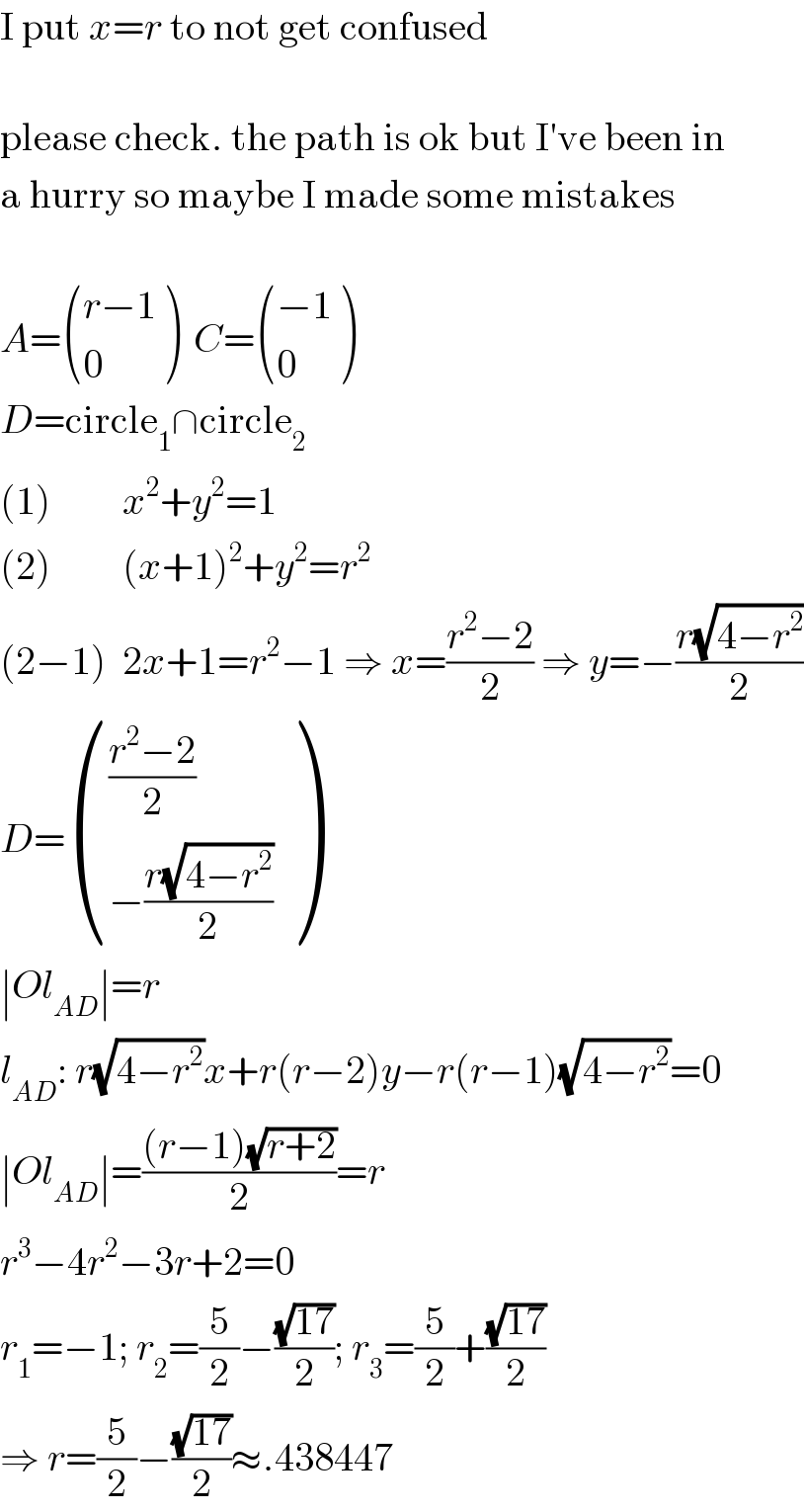
$$\mathrm{I}\:\mathrm{put}\:{x}={r}\:\mathrm{to}\:\mathrm{not}\:\mathrm{get}\:\mathrm{confused} \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{check}.\:\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{ok}\:\mathrm{but}\:\mathrm{I}'\mathrm{ve}\:\mathrm{been}\:\mathrm{in} \\ $$$$\mathrm{a}\:\mathrm{hurry}\:\mathrm{so}\:\mathrm{maybe}\:\mathrm{I}\:\mathrm{made}\:\mathrm{some}\:\mathrm{mistakes} \\ $$$$ \\ $$$${A}=\begin{pmatrix}{{r}−\mathrm{1}}\\{\mathrm{0}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{0}}\end{pmatrix} \\ $$$${D}=\mathrm{circle}_{\mathrm{1}} \cap\mathrm{circle}_{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}−\mathrm{1}\right)\:\:\mathrm{2}{x}+\mathrm{1}={r}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow\:{x}=\frac{{r}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}}\:\Rightarrow\:{y}=−\frac{{r}\sqrt{\mathrm{4}−{r}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${D}=\begin{pmatrix}{\frac{{r}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}}}\\{−\frac{{r}\sqrt{\mathrm{4}−{r}^{\mathrm{2}} }}{\mathrm{2}}}\end{pmatrix} \\ $$$$\mid{Ol}_{{AD}} \mid={r} \\ $$$${l}_{{AD}} :\:{r}\sqrt{\mathrm{4}−{r}^{\mathrm{2}} }{x}+{r}\left({r}−\mathrm{2}\right){y}−{r}\left({r}−\mathrm{1}\right)\sqrt{\mathrm{4}−{r}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\mid{Ol}_{{AD}} \mid=\frac{\left({r}−\mathrm{1}\right)\sqrt{{r}+\mathrm{2}}}{\mathrm{2}}={r} \\ $$$${r}^{\mathrm{3}} −\mathrm{4}{r}^{\mathrm{2}} −\mathrm{3}{r}+\mathrm{2}=\mathrm{0} \\ $$$${r}_{\mathrm{1}} =−\mathrm{1};\:{r}_{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{2}}−\frac{\sqrt{\mathrm{17}}}{\mathrm{2}};\:{r}_{\mathrm{3}} =\frac{\mathrm{5}}{\mathrm{2}}+\frac{\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{r}=\frac{\mathrm{5}}{\mathrm{2}}−\frac{\sqrt{\mathrm{17}}}{\mathrm{2}}\approx.\mathrm{438447} \\ $$
Commented by MJS last updated on 24/Oct/18

$$\mathrm{ok}\:\mathrm{thank}\:\mathrm{you}. \\ $$
Commented by ajfour last updated on 24/Oct/18
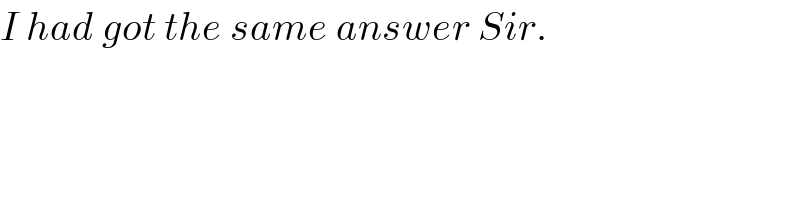
$${I}\:{had}\:{got}\:{the}\:{same}\:{answer}\:{Sir}. \\ $$
