
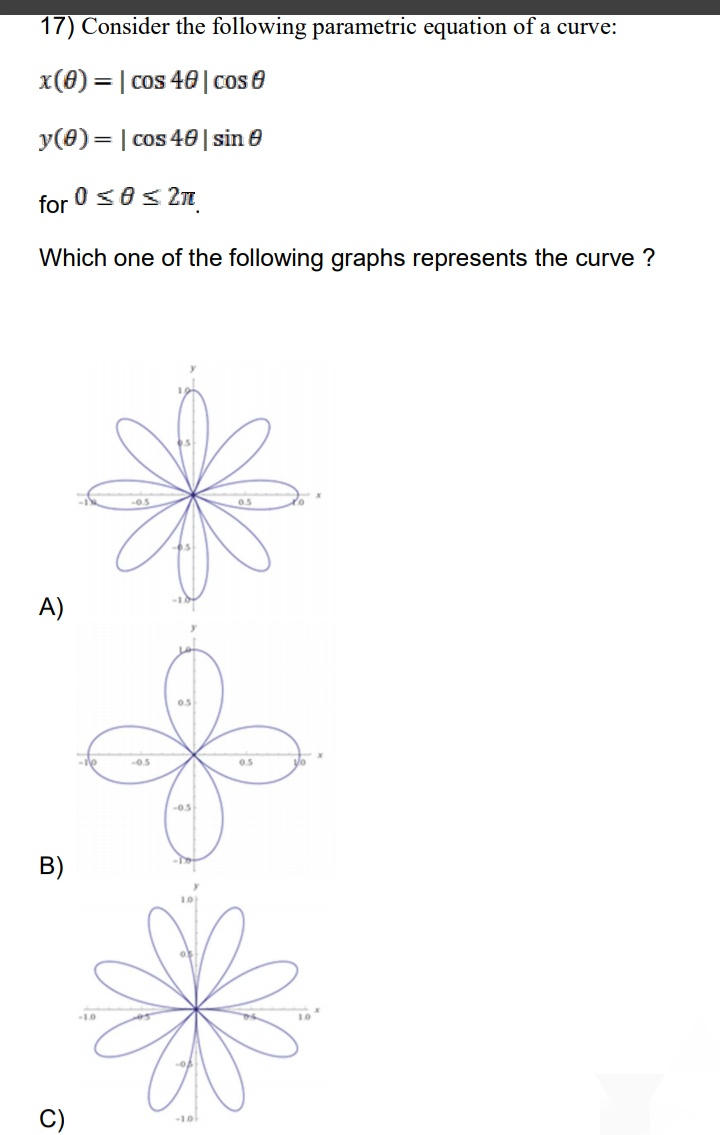
Question Number 46252 by rahul 19 last updated on 23/Oct/18
Answered by MJS last updated on 23/Oct/18
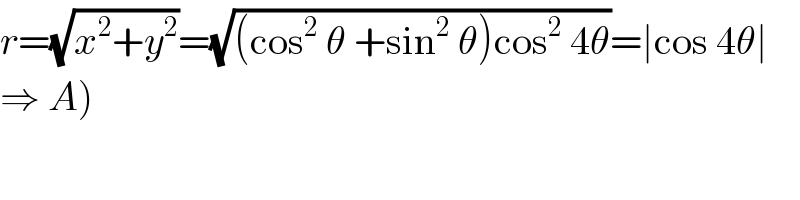
$${r}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\sqrt{\left(\mathrm{cos}^{\mathrm{2}} \:\theta\:+\mathrm{sin}^{\mathrm{2}} \:\theta\right)\mathrm{cos}^{\mathrm{2}} \:\mathrm{4}\theta}=\mid\mathrm{cos}\:\mathrm{4}\theta\mid \\ $$$$\left.\Rightarrow\:{A}\right) \\ $$
Commented by rahul 19 last updated on 23/Oct/18

$${thanks}\:{sir}. \\ $$
Answered by ajfour last updated on 23/Oct/18
![r = (√(x^2 +y^2 )) = ∣cos 4θ∣ r=r_(max) =1 ⇒ cos 4θ = ±1 for θ ∈ [0, 2π] θ= 0, (π/4), (π/2), ((3π)/4), π,((5π)/4), ((3π)/2),((7π)/4) hence (A).](Q46275.png)
$${r}\:=\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\:\mid\mathrm{cos}\:\mathrm{4}\theta\mid \\ $$$${r}={r}_{{max}} =\mathrm{1}\:\Rightarrow\:\mathrm{cos}\:\mathrm{4}\theta\:=\:\pm\mathrm{1} \\ $$$${for}\:\:\:\theta\:\in\:\left[\mathrm{0},\:\mathrm{2}\pi\right] \\ $$$$\:\:\:\theta=\:\mathrm{0},\:\frac{\pi}{\mathrm{4}},\:\frac{\pi}{\mathrm{2}},\:\frac{\mathrm{3}\pi}{\mathrm{4}},\:\pi,\frac{\mathrm{5}\pi}{\mathrm{4}},\:\frac{\mathrm{3}\pi}{\mathrm{2}},\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$$${hence}\:\:\left({A}\right). \\ $$
Commented by rahul 19 last updated on 23/Oct/18

$${ok}\:{sir}... \\ $$
Commented by rahul 19 last updated on 23/Oct/18

$${thanks}\:{sir}. \\ $$
Commented by rahul 19 last updated on 23/Oct/18

$${Why}\:{option}\:\left({B}\right)\:{is}\:{wrong}\:? \\ $$
Commented by MJS last updated on 23/Oct/18
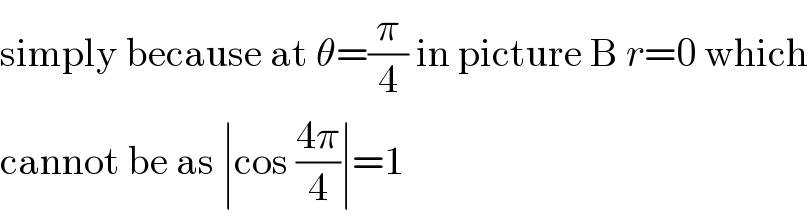
$$\mathrm{simply}\:\mathrm{because}\:\mathrm{at}\:\theta=\frac{\pi}{\mathrm{4}}\:\mathrm{in}\:\mathrm{picture}\:\mathrm{B}\:{r}=\mathrm{0}\:\mathrm{which} \\ $$$$\mathrm{cannot}\:\mathrm{be}\:\mathrm{as}\:\mid\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{4}}\mid=\mathrm{1} \\ $$
