Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 46238 by Meritguide1234 last updated on 23/Oct/18

Commented by math1967 last updated on 23/Oct/18

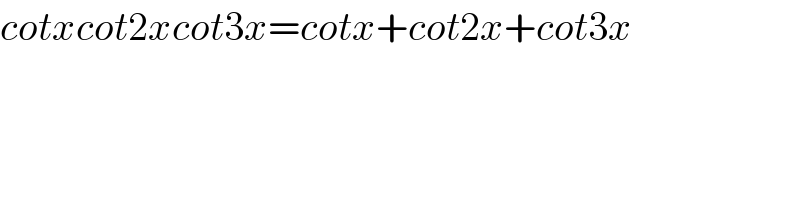
cotxcot2xcot3x=cotx+cot2x+cot3x

$${cotxcot}\mathrm{2}{xcot}\mathrm{3}{x}={cotx}+{cot}\mathrm{2}{x}+{cot}\mathrm{3}{x} \\ $$

Commented by Meritguide1234 last updated on 23/Oct/18

no

$${no} \\ $$

Commented by math1967 last updated on 23/Oct/18

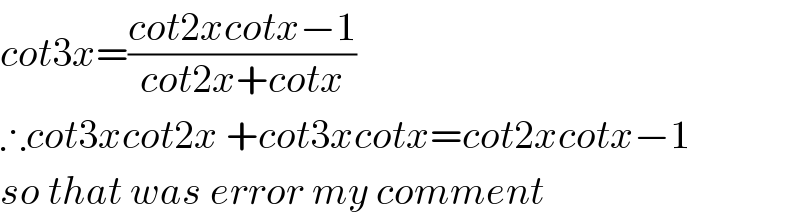
cot3x=((cot2xcotx−1)/(cot2x+cotx)) ∴cot3xcot2x +cot3xcotx=cot2xcotx−1 so that was error my comment

$${cot}\mathrm{3}{x}=\frac{{cot}\mathrm{2}{xcotx}−\mathrm{1}}{{cot}\mathrm{2}{x}+{cotx}} \\ $$$$\therefore{cot}\mathrm{3}{xcot}\mathrm{2}{x}\:+{cot}\mathrm{3}{xcotx}={cot}\mathrm{2}{xcotx}−\mathrm{1} \\ $$$${so}\:{that}\:{was}\:{error}\:{my}\:{comment} \\ $$

Commented by MJS last updated on 23/Oct/18

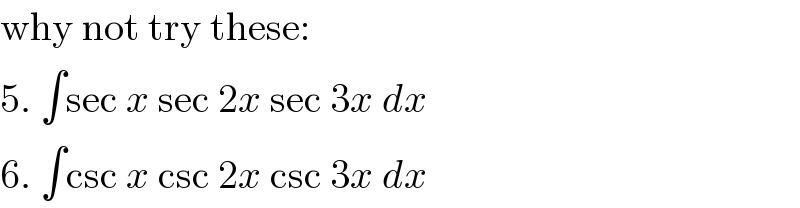
why not try these: 5. ∫sec x sec 2x sec 3x dx 6. ∫csc x csc 2x csc 3x dx

$$\mathrm{why}\:\mathrm{not}\:\mathrm{try}\:\mathrm{these}: \\ $$$$\mathrm{5}.\:\int\mathrm{sec}\:{x}\:\mathrm{sec}\:\mathrm{2}{x}\:\mathrm{sec}\:\mathrm{3}{x}\:{dx} \\ $$$$\mathrm{6}.\:\int\mathrm{csc}\:{x}\:\mathrm{csc}\:\mathrm{2}{x}\:\mathrm{csc}\:\mathrm{3}{x}\:{dx} \\ $$

Commented by Meritguide1234 last updated on 23/Oct/18

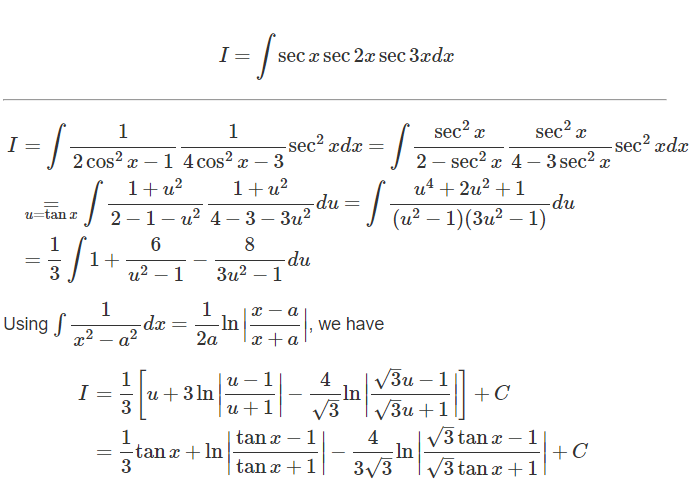
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Oct/18

3)tan3x=tan(x+2x) =((tanx+tan2x)/(1−tanx.tan2x)) tan3x−tanxtan2xtan3x=tanx+tan2x tan3x−tanx−tan2x=tanxtan2xtan3x so∫tanxtan2xtan3xdx =∫(tan3x−tan2x−tanx) dx =(1/3)×lnsec3x−(1/2)×lnsec2x−lnsecx +c =corrected

$$\left.\mathrm{3}\right){tan}\mathrm{3}{x}={tan}\left({x}+\mathrm{2}{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{tanx}+{tan}\mathrm{2}{x}}{\mathrm{1}−{tanx}.{tan}\mathrm{2}{x}} \\ $$$${tan}\mathrm{3}{x}−{tanxtan}\mathrm{2}{xtan}\mathrm{3}{x}={tanx}+{tan}\mathrm{2}{x} \\ $$$${tan}\mathrm{3}{x}−{tanx}−{tan}\mathrm{2}{x}={tanxtan}\mathrm{2}{xtan}\mathrm{3}{x} \\ $$$${so}\int{tanxtan}\mathrm{2}{xtan}\mathrm{3}{xdx} \\ $$$$=\int\left({tan}\mathrm{3}{x}−{tan}\mathrm{2}{x}−{tanx}\right)\:\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×{lnsec}\mathrm{3}{x}−\frac{\mathrm{1}}{\mathrm{2}}×{lnsec}\mathrm{2}{x}−{lnsecx}\:\:+{c} \\ $$$$={corrected} \\ $$

Commented by Meritguide1234 last updated on 23/Oct/18

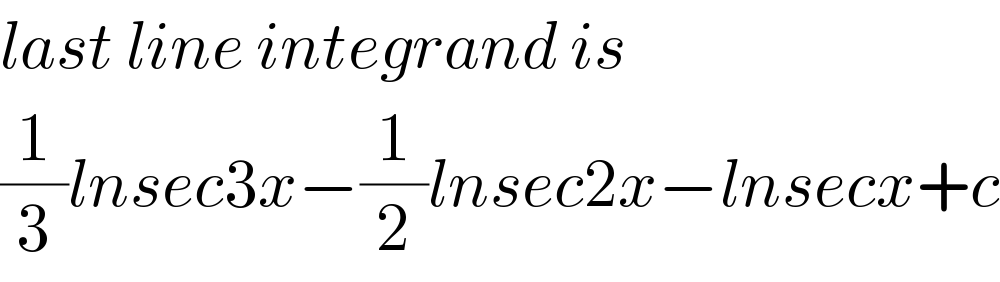
last line integrand is (1/3)lnsec3x−(1/2)lnsec2x−lnsecx+c

$${last}\:{line}\:{integrand}\:{is}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{lnsec}\mathrm{3}{x}−\frac{\mathrm{1}}{\mathrm{2}}{lnsec}\mathrm{2}{x}−{lnsecx}+{c} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 23/Oct/18

yes in hurry...

$${yes}\:{in}\:{hurry}... \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 23/Oct/18

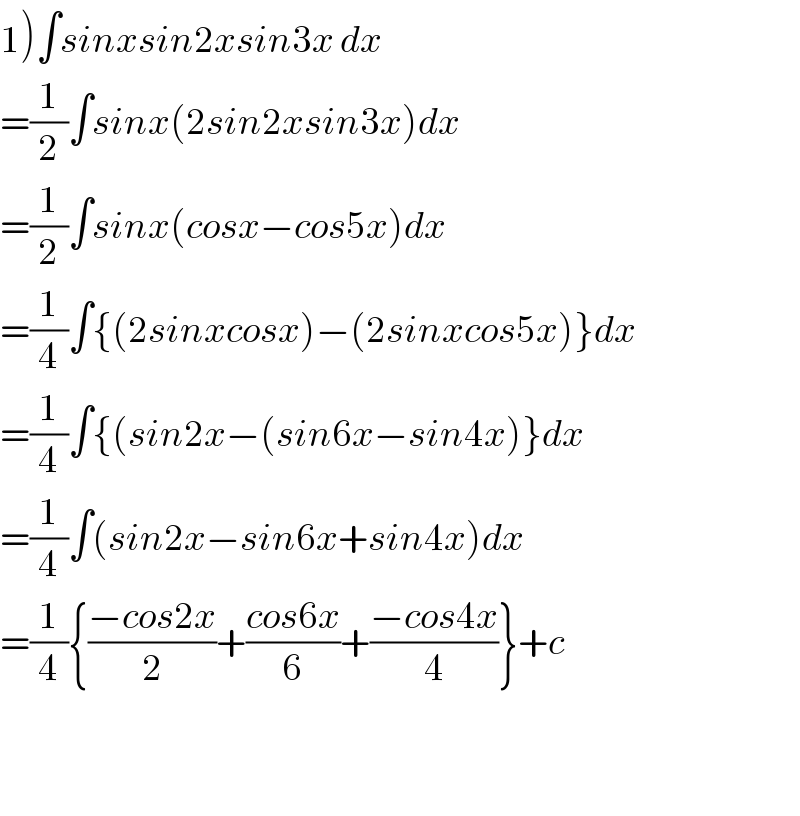
1)∫sinxsin2xsin3x dx =(1/2)∫sinx(2sin2xsin3x)dx =(1/2)∫sinx(cosx−cos5x)dx =(1/4)∫{(2sinxcosx)−(2sinxcos5x)}dx =(1/4)∫{(sin2x−(sin6x−sin4x)}dx =(1/4)∫(sin2x−sin6x+sin4x)dx =(1/4){((−cos2x)/2)+((cos6x)/6)+((−cos4x)/4)}+c

$$\left.\mathrm{1}\right)\int{sinxsin}\mathrm{2}{xsin}\mathrm{3}{x}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{sinx}\left(\mathrm{2}{sin}\mathrm{2}{xsin}\mathrm{3}{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{sinx}\left({cosx}−{cos}\mathrm{5}{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left\{\left(\mathrm{2}{sinxcosx}\right)−\left(\mathrm{2}{sinxcos}\mathrm{5}{x}\right)\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left\{\left({sin}\mathrm{2}{x}−\left({sin}\mathrm{6}{x}−{sin}\mathrm{4}{x}\right)\right\}{dx}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left({sin}\mathrm{2}{x}−{sin}\mathrm{6}{x}+{sin}\mathrm{4}{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{−{cos}\mathrm{2}{x}}{\mathrm{2}}+\frac{{cos}\mathrm{6}{x}}{\mathrm{6}}+\frac{−{cos}\mathrm{4}{x}}{\mathrm{4}}\right\}+{c} \\ $$$$ \\ $$$$ \\ $$

Commented by Meritguide1234 last updated on 23/Oct/18

correct

$${correct} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 23/Oct/18

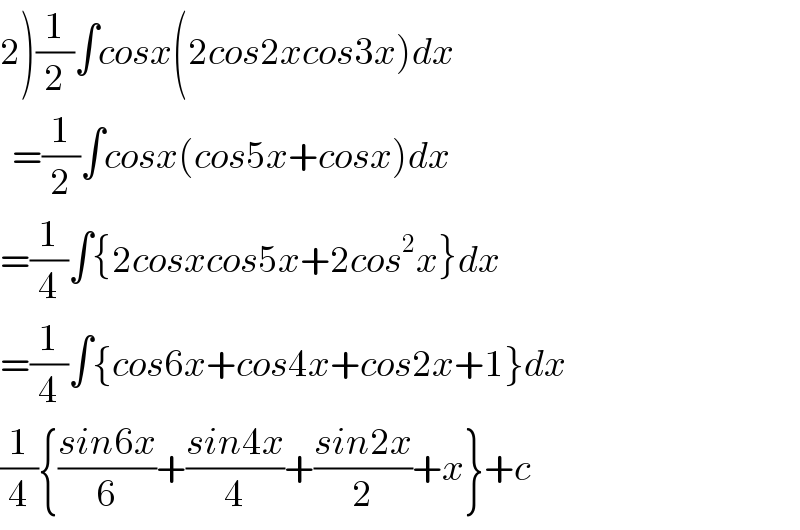
2)(1/2)∫cosx(2cos2xcos3x)dx =(1/2)∫cosx(cos5x+cosx)dx =(1/4)∫{2cosxcos5x+2cos^2 x}dx =(1/4)∫{cos6x+cos4x+cos2x+1}dx (1/4){((sin6x)/6)+((sin4x)/4)+((sin2x)/2)+x}+c

$$\left.\mathrm{2}\right)\frac{\mathrm{1}}{\mathrm{2}}\int{cosx}\left(\mathrm{2}{cos}\mathrm{2}{xcos}\mathrm{3}{x}\right){dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int{cosx}\left({cos}\mathrm{5}{x}+{cosx}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left\{\mathrm{2}{cosxcos}\mathrm{5}{x}+\mathrm{2}{cos}^{\mathrm{2}} {x}\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left\{{cos}\mathrm{6}{x}+{cos}\mathrm{4}{x}+{cos}\mathrm{2}{x}+\mathrm{1}\right\}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{{sin}\mathrm{6}{x}}{\mathrm{6}}+\frac{{sin}\mathrm{4}{x}}{\mathrm{4}}+\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}+{x}\right\}+{c} \\ $$

Commented by Meritguide1234 last updated on 23/Oct/18

correct...try no 4

$${correct}...{try}\:{no}\:\mathrm{4} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 23/Oct/18

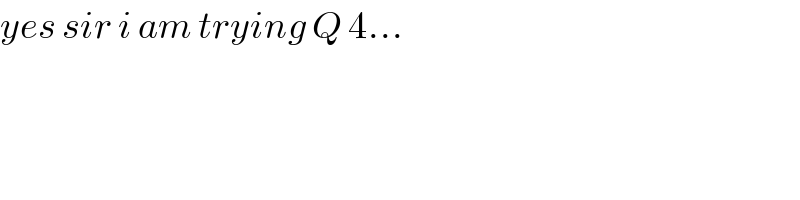
yes sir i am trying Q 4...

$${yes}\:{sir}\:{i}\:{am}\:{trying}\:{Q}\:\mathrm{4}... \\ $$

Answered by MJS last updated on 23/Oct/18

∫cot x cot 2x cot 3x dx= =∫(cot x ×((cos^2 x −sin^2 x)/(2cos x sin x))×((cos x (cos^2 x −3sin^2 x))/(sin x (3cos^2 x −sin^2 x)))dx= [cos x =((cot x)/(csc x)); sin x =(1/(csc x)); csc^2 x =1+cot^2 x] =∫((csc^2 x cot x (cot^4 x −4cot^2 x +3))/(2(3cot^4 x +2cot^2 x −1)))dx= [t=cot x → dx=−(dt/(csc^2 x))] =−(1/2)∫((t(t^4 −4t^2 +3))/(3t^4 +2t^2 −1))dt=−(1/6)∫tdt+(1/3)∫((t(7t^2 −5))/(3t^4 +2t^2 −1))dt −(1/6)∫tdt=−(t^2 /(12))=−((cot^2 x)/(12)) (1/3)∫((t(7t^2 −5))/(3t^4 +2t^2 −1))dt=∫(t/(t^2 +1))dt−(2/3)∫(t/(3t^2 −1))dt ∫(t/(t^2 +1))dt=(1/2)ln (t^2 +1) =(1/2)ln (1+cot^2 x) =ln ∣csc x∣ −(2/3)∫(t/(3t^2 −1))dt=−(1/9)ln (3t^2 −1)=−(1/9)ln ∣1−3cot^2 x∣ ∫cot x cot 2x cot 3x dx= =ln ∣csc x∣ −(1/9)ln ∣1−3cot^2 x∣ −((cot^2 x)/(12))+C

$$\int\mathrm{cot}\:{x}\:\mathrm{cot}\:\mathrm{2}{x}\:\mathrm{cot}\:\mathrm{3}{x}\:{dx}= \\ $$$$=\int\left(\mathrm{cot}\:{x}\:×\frac{\mathrm{cos}^{\mathrm{2}} \:{x}\:−\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{2cos}\:{x}\:\mathrm{sin}\:{x}}×\frac{\mathrm{cos}\:{x}\:\left(\mathrm{cos}^{\mathrm{2}} \:{x}\:−\mathrm{3sin}^{\mathrm{2}} \:{x}\right)}{\mathrm{sin}\:{x}\:\left(\mathrm{3cos}^{\mathrm{2}} \:{x}\:−\mathrm{sin}^{\mathrm{2}} \:{x}\right.}\right){dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{cos}\:{x}\:=\frac{\mathrm{cot}\:{x}}{\mathrm{csc}\:{x}};\:\mathrm{sin}\:{x}\:=\frac{\mathrm{1}}{\mathrm{csc}\:{x}};\:\mathrm{csc}^{\mathrm{2}} \:{x}\:=\mathrm{1}+\mathrm{cot}^{\mathrm{2}} \:{x}\right] \\ $$$$=\int\frac{\mathrm{csc}^{\mathrm{2}} \:{x}\:\mathrm{cot}\:{x}\:\left(\mathrm{cot}^{\mathrm{4}} \:{x}\:−\mathrm{4cot}^{\mathrm{2}} \:{x}\:+\mathrm{3}\right)}{\mathrm{2}\left(\mathrm{3cot}^{\mathrm{4}} \:{x}\:+\mathrm{2cot}^{\mathrm{2}} \:{x}\:−\mathrm{1}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cot}\:{x}\:\rightarrow\:{dx}=−\frac{{dt}}{\mathrm{csc}^{\mathrm{2}} \:{x}}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{t}\left({t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{3}{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}}{dt}=−\frac{\mathrm{1}}{\mathrm{6}}\int{tdt}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{t}\left(\mathrm{7}{t}^{\mathrm{2}} −\mathrm{5}\right)}{\mathrm{3}{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$ \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{6}}\int{tdt}=−\frac{{t}^{\mathrm{2}} }{\mathrm{12}}=−\frac{\mathrm{cot}^{\mathrm{2}} \:{x}}{\mathrm{12}} \\ $$$$ \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{t}\left(\mathrm{7}{t}^{\mathrm{2}} −\mathrm{5}\right)}{\mathrm{3}{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}}{dt}=\int\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{t}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\int\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{cot}^{\mathrm{2}} \:{x}\right)\:=\mathrm{ln}\:\mid\mathrm{csc}\:{x}\mid \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{t}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}{dt}=−\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right)=−\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\mid\mathrm{1}−\mathrm{3cot}^{\mathrm{2}} \:{x}\mid \\ $$$$ \\ $$$$\int\mathrm{cot}\:{x}\:\mathrm{cot}\:\mathrm{2}{x}\:\mathrm{cot}\:\mathrm{3}{x}\:{dx}= \\ $$$$=\mathrm{ln}\:\mid\mathrm{csc}\:{x}\mid\:−\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\mid\mathrm{1}−\mathrm{3cot}^{\mathrm{2}} \:{x}\mid\:−\frac{\mathrm{cot}^{\mathrm{2}} \:{x}}{\mathrm{12}}+{C} \\ $$

Commented by Meritguide1234 last updated on 23/Oct/18

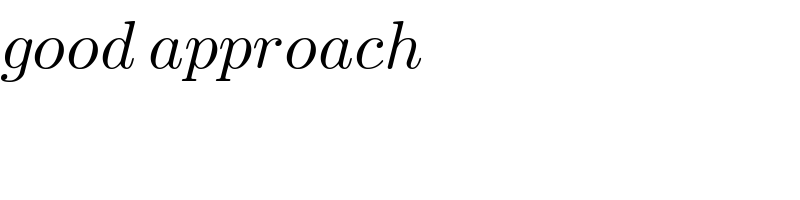
good approach

$${good}\:{approach} \\ $$

Commented by Meritguide1234 last updated on 23/Oct/18

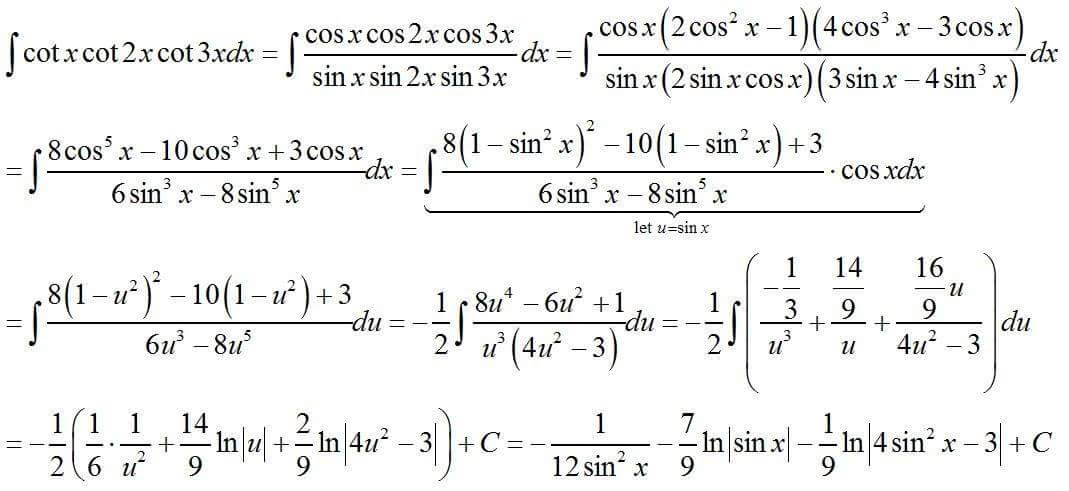
Commented by Meritguide1234 last updated on 23/Oct/18

Terms of Service

Privacy Policy

Contact: info@tinkutara.com