Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 46110 by Tawa1 last updated on 21/Oct/18

Commented by math khazana by abdo last updated on 22/Oct/18

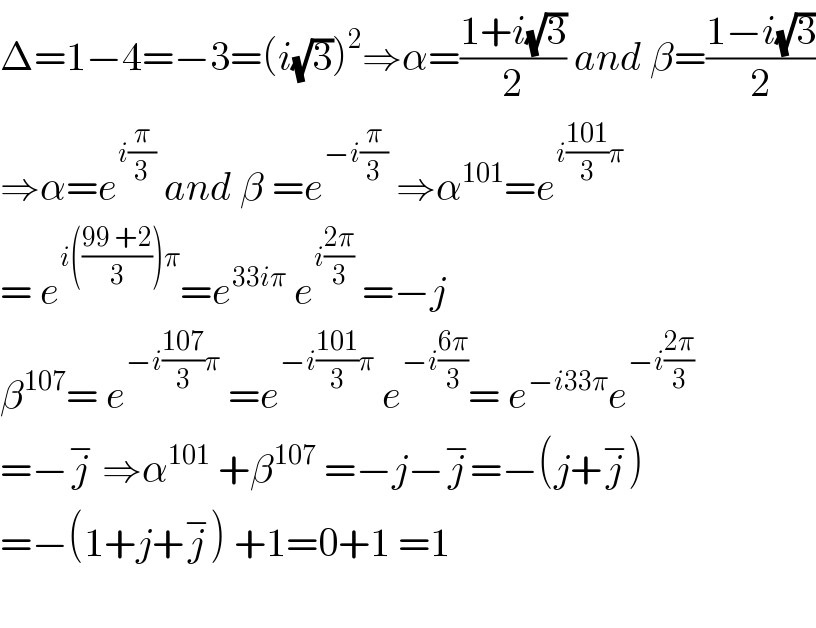
Δ=1−4=−3=(i(√3))^2 ⇒α=((1+i(√3))/2) and β=((1−i(√3))/2) ⇒α=e^(i(π/3)) and β =e^(−i(π/3)) ⇒α^(101) =e^(i((101)/3)π) = e^(i(((99 +2)/3))π) =e^(33iπ) e^(i((2π)/3)) =−j β^(107) = e^(−i((107)/3)π) =e^(−i((101)/3)π) e^(−i((6π)/3)) = e^(−i33π) e^(−i((2π)/3)) =−j^− ⇒α^(101) +β^(107) =−j−j^− =−(j+j^− ) =−(1+j+j^− ) +1=0+1 =1

$$\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \Rightarrow\alpha=\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:{and}\:\beta=\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\alpha={e}^{{i}\frac{\pi}{\mathrm{3}}} \:{and}\:\beta\:={e}^{−{i}\frac{\pi}{\mathrm{3}}} \:\Rightarrow\alpha^{\mathrm{101}} ={e}^{{i}\frac{\mathrm{101}}{\mathrm{3}}\pi} \\ $$$$=\:{e}^{{i}\left(\frac{\mathrm{99}\:+\mathrm{2}}{\mathrm{3}}\right)\pi} ={e}^{\mathrm{33}{i}\pi} \:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:=−{j} \\ $$$$\beta^{\mathrm{107}} =\:{e}^{−{i}\frac{\mathrm{107}}{\mathrm{3}}\pi} \:={e}^{−{i}\frac{\mathrm{101}}{\mathrm{3}}\pi} \:{e}^{−{i}\frac{\mathrm{6}\pi}{\mathrm{3}}} =\:{e}^{−{i}\mathrm{33}\pi} {e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$=−\overset{−} {{j}}\:\Rightarrow\alpha^{\mathrm{101}} \:+\beta^{\mathrm{107}} \:=−{j}−\overset{−} {{j}}=−\left({j}+\overset{−} {{j}}\right) \\ $$$$=−\left(\mathrm{1}+{j}+\overset{−} {{j}}\right)\:+\mathrm{1}=\mathrm{0}+\mathrm{1}\:=\mathrm{1} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 22/Oct/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 21/Oct/18

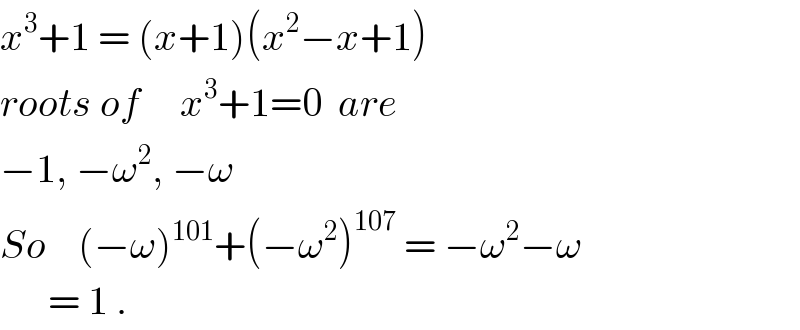
x^3 +1 = (x+1)(x^2 −x+1) roots of x^3 +1=0 are −1, −ω^2 , −ω So (−ω)^(101) +(−ω^2 )^(107) = −ω^2 −ω = 1 .

$${x}^{\mathrm{3}} +\mathrm{1}\:=\:\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$${roots}\:{of}\:\:\:\:\:{x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0}\:\:{are} \\ $$$$−\mathrm{1},\:−\omega^{\mathrm{2}} ,\:−\omega \\ $$$${So}\:\:\:\:\left(−\omega\right)^{\mathrm{101}} +\left(−\omega^{\mathrm{2}} \right)^{\mathrm{107}} \:=\:−\omega^{\mathrm{2}} −\omega \\ $$$$\:\:\:\:\:\:=\:\mathrm{1}\:. \\ $$

Commented by Tawa1 last updated on 21/Oct/18

God bless you sir. but i don′t really understand sir. from the (− ω) and the substitution to get 1

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{but}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{really}\:\mathrm{understand}\:\mathrm{sir}.\:\:\mathrm{from}\:\mathrm{the}\:\:\left(−\:\omega\right) \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{substitution}\:\mathrm{to}\:\mathrm{get}\:\:\mathrm{1} \\ $$

Commented by $@ty@m last updated on 21/Oct/18

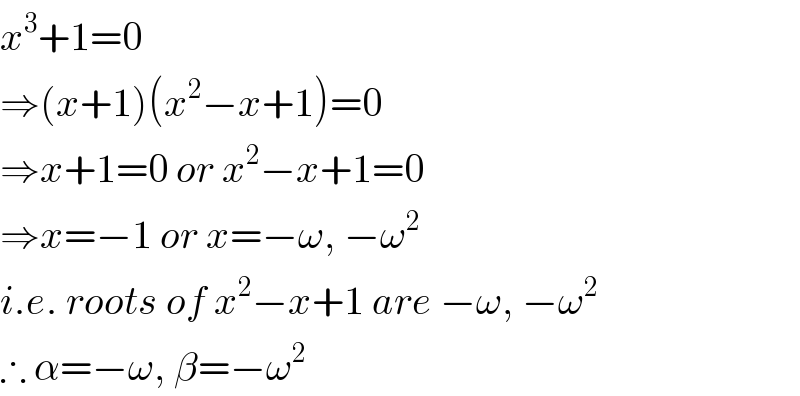
x^3 +1=0 ⇒(x+1)(x^2 −x+1)=0 ⇒x+1=0 or x^2 −x+1=0 ⇒x=−1 or x=−ω, −ω^2 i.e. roots of x^2 −x+1 are −ω, −ω^2 ∴ α=−ω, β=−ω^2

$${x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}+\mathrm{1}=\mathrm{0}\:{or}\:{x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{1}\:{or}\:{x}=−\omega,\:−\omega^{\mathrm{2}} \\ $$$${i}.{e}.\:{roots}\:{of}\:{x}^{\mathrm{2}} −{x}+\mathrm{1}\:{are}\:−\omega,\:−\omega^{\mathrm{2}} \\ $$$$\therefore\:\alpha=−\omega,\:\beta=−\omega^{\mathrm{2}} \\ $$

Commented by Tawa1 last updated on 21/Oct/18

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com