Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 46042 by naka3546 last updated on 20/Oct/18

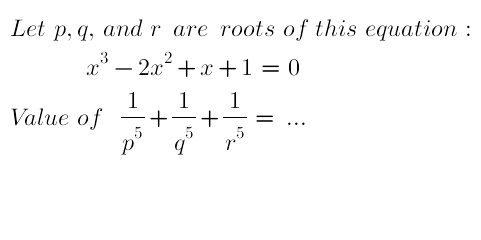
Commented by Tawa1 last updated on 20/Oct/18

Sir, can you share me the link to download this pdf or how can i get it sir

$$\mathrm{Sir},\:\mathrm{can}\:\mathrm{you}\:\mathrm{share}\:\mathrm{me}\:\mathrm{the}\:\mathrm{link}\:\mathrm{to}\:\mathrm{download}\:\mathrm{this}\:\mathrm{pdf}\:\mathrm{or}\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{get}\:\mathrm{it}\:\mathrm{sir} \\ $$

Commented by Kunal12588 last updated on 20/Oct/18

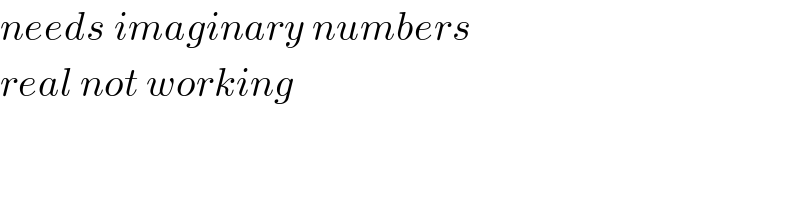
needs imaginary numbers real not working

$${needs}\:{imaginary}\:{numbers}\: \\ $$$${real}\:{not}\:{working} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

i have checked Hall and knight higher algebra and Bernard and child ...found some theorem i have solved the problem tsking help...

$${i}\:{have}\:{checked}\:{Hall}\:{and}\:{knight}\:{higher}\:{algebra} \\ $$$${and}\:{Bernard}\:{and}\:{child}\:...{found}\:{some}\:{theorem} \\ $$$${i}\:{have}\:{solved}\:{the}\:{problem}\:{tsking}\:{help}... \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

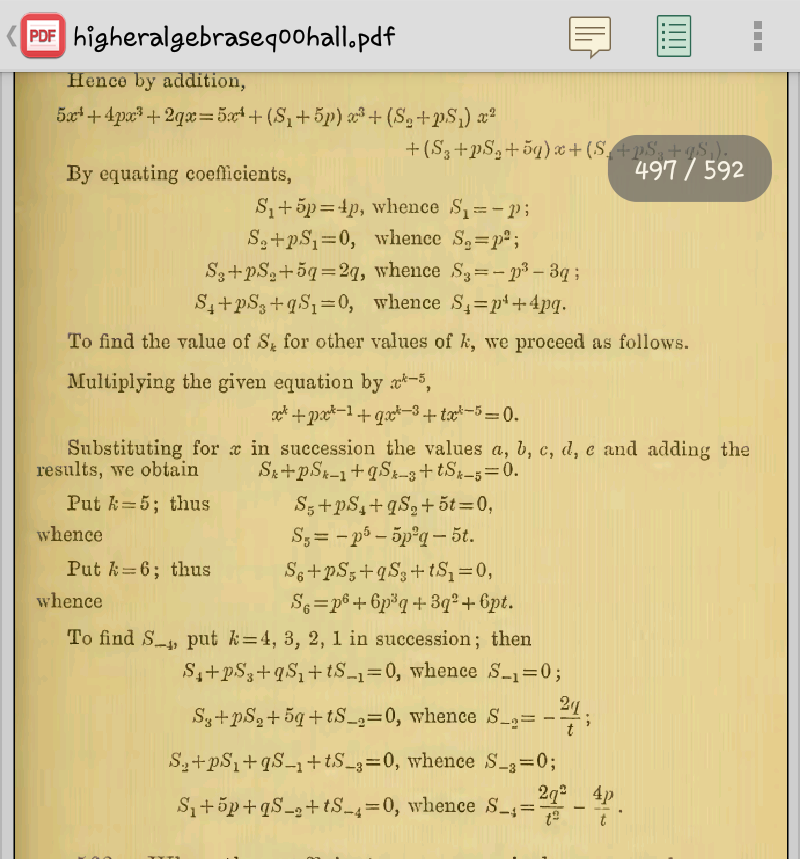
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

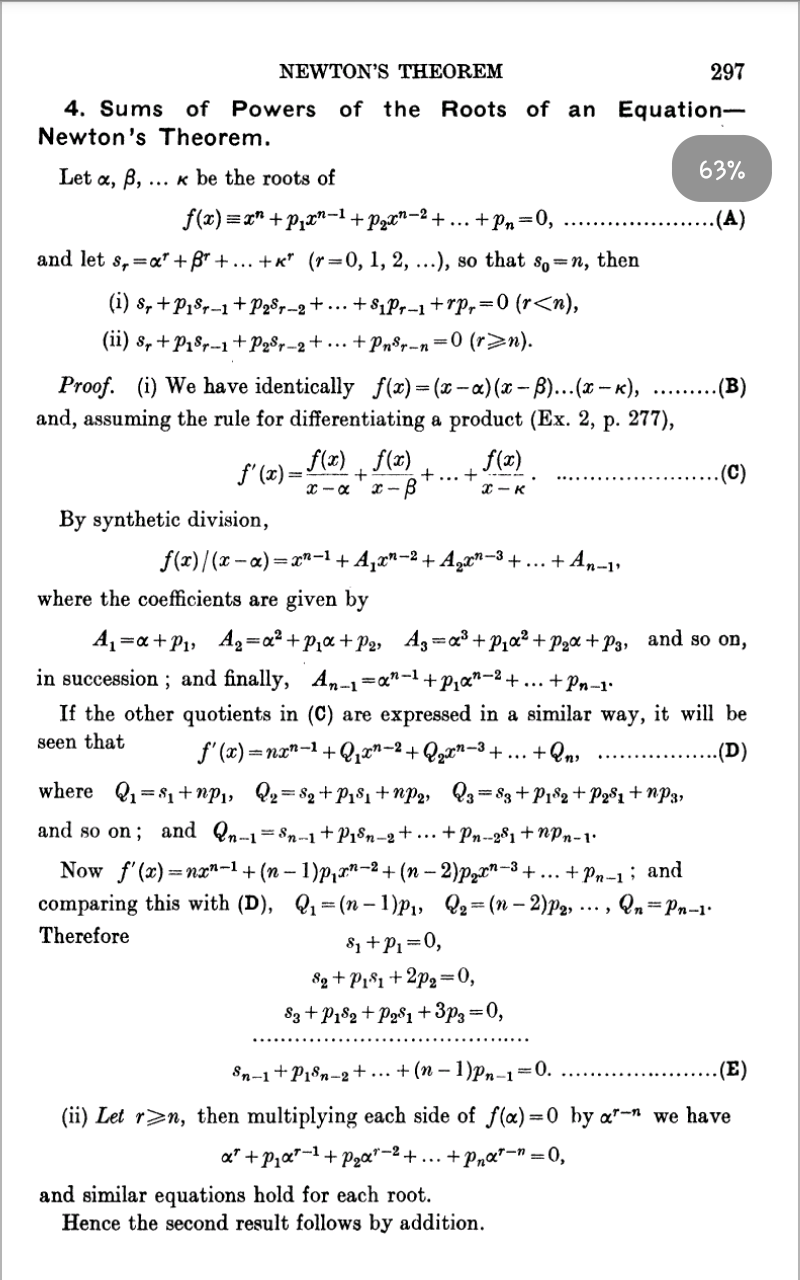
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

Commented by Tawa1 last updated on 20/Oct/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by MJS last updated on 20/Oct/18

hope this helps: we can write the solutions of any polynome of 3^(rd) degree with real factors as x_1 =t ⇒ x_1 ^5 =t^5 x_2 =re^(iα) ⇒ x_2 ^5 =r^5 e^(5iα) x_3 =re^(−iα) ⇒ x_3 ^5 =r^5 e^(−5iα) (1/x_1 ^5 )+(1/x_2 ^5 )+(1/x_3 ^5 )=t^(−5) +r^(−5) (e^(5iα) +e^(−5iα) )= =(1/t^5 )+(2/r^5 )cos 5α and this is a real number

$$\mathrm{hope}\:\mathrm{this}\:\mathrm{helps}: \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{write}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{any}\:\mathrm{polynome} \\ $$$$\mathrm{of}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{with}\:\mathrm{real}\:\mathrm{factors}\:\mathrm{as} \\ $$$${x}_{\mathrm{1}} ={t}\:\Rightarrow\:{x}_{\mathrm{1}} ^{\mathrm{5}} ={t}^{\mathrm{5}} \\ $$$${x}_{\mathrm{2}} ={r}\mathrm{e}^{\mathrm{i}\alpha} \:\Rightarrow\:\:{x}_{\mathrm{2}} ^{\mathrm{5}} ={r}^{\mathrm{5}} \mathrm{e}^{\mathrm{5i}\alpha} \\ $$$${x}_{\mathrm{3}} ={r}\mathrm{e}^{−\mathrm{i}\alpha} \:\Rightarrow\:{x}_{\mathrm{3}} ^{\mathrm{5}} ={r}^{\mathrm{5}} \mathrm{e}^{−\mathrm{5i}\alpha} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{x}_{\mathrm{1}} ^{\mathrm{5}} }+\frac{\mathrm{1}}{{x}_{\mathrm{2}} ^{\mathrm{5}} }+\frac{\mathrm{1}}{{x}_{\mathrm{3}} ^{\mathrm{5}} }={t}^{−\mathrm{5}} +{r}^{−\mathrm{5}} \left(\mathrm{e}^{\mathrm{5i}\alpha} +\mathrm{e}^{−\mathrm{5i}\alpha} \right)= \\ $$$$=\frac{\mathrm{1}}{{t}^{\mathrm{5}} }+\frac{\mathrm{2}}{{r}^{\mathrm{5}} }\mathrm{cos}\:\mathrm{5}\alpha\:\:\:\:\:\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{real}\:\mathrm{number} \\ $$

Answered by ajfour last updated on 20/Oct/18

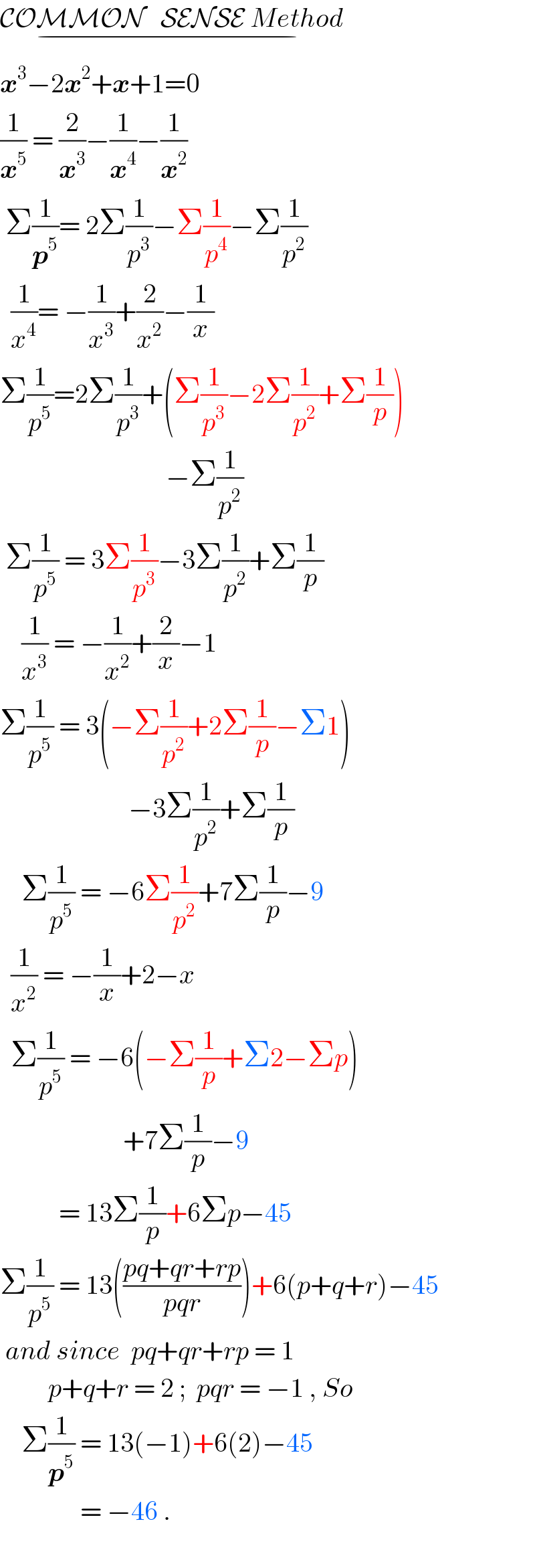
COMMON SENSE Method _(−) x^3 −2x^2 +x+1=0 (1/x^5 ) = (2/x^3 )−(1/x^4 )−(1/x^2 ) Σ(1/p^5 )= 2Σ(1/p^3 )−Σ(1/p^4 )−Σ(1/p^2 ) (1/x^4 )= −(1/x^3 )+(2/x^2 )−(1/x) Σ(1/p^5 )=2Σ(1/p^3 )+(Σ(1/p^3 )−2Σ(1/p^2 )+Σ(1/p)) −Σ(1/p^2 ) Σ(1/p^5 ) = 3Σ(1/p^3 )−3Σ(1/p^2 )+Σ(1/p) (1/x^3 ) = −(1/x^2 )+(2/x)−1 Σ(1/p^5 ) = 3(−Σ(1/p^2 )+2Σ(1/p)−Σ1) −3Σ(1/p^2 )+Σ(1/p) Σ(1/p^5 ) = −6Σ(1/p^2 )+7Σ(1/p)−9 (1/x^2 ) = −(1/x)+2−x Σ(1/p^5 ) = −6(−Σ(1/p)+Σ2−Σp) +7Σ(1/p)−9 = 13Σ(1/p)+6Σp−45 Σ(1/p^5 ) = 13(((pq+qr+rp)/(pqr)))+6(p+q+r)−45 and since pq+qr+rp = 1 p+q+r = 2 ; pqr = −1 , So Σ(1/p^5 ) = 13(−1)+6(2)−45 = −46 .

$$\underset{−} {\mathcal{COMMON}\:\:\:\mathcal{SENSE}\:{Method}\:} \\ $$$$\boldsymbol{{x}}^{\mathrm{3}} −\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{5}} }\:=\:\frac{\mathrm{2}}{\boldsymbol{{x}}^{\mathrm{3}} }−\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{4}} }−\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} } \\ $$$$\:\Sigma\frac{\mathrm{1}}{\boldsymbol{{p}}^{\mathrm{5}} }=\:\mathrm{2}\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{3}} }−\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{4}} }−\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{2}} } \\ $$$$\:\:\frac{\mathrm{1}}{{x}^{\mathrm{4}} }=\:−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}} \\ $$$$\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{5}} }=\mathrm{2}\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{3}} }+\left(\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{3}} }−\mathrm{2}\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\Sigma\frac{\mathrm{1}}{{p}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{2}} } \\ $$$$\:\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{5}} }\:=\:\mathrm{3}\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{3}} }−\mathrm{3}\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\Sigma\frac{\mathrm{1}}{{p}} \\ $$$$\:\:\:\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:=\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{2}}{{x}}−\mathrm{1} \\ $$$$\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{5}} }\:=\:\mathrm{3}\left(−\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\mathrm{2}\Sigma\frac{\mathrm{1}}{{p}}−\Sigma\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\Sigma\frac{\mathrm{1}}{{p}} \\ $$$$\:\:\:\:\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{5}} }\:=\:−\mathrm{6}\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\mathrm{7}\Sigma\frac{\mathrm{1}}{{p}}−\mathrm{9} \\ $$$$\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:=\:−\frac{\mathrm{1}}{{x}}+\mathrm{2}−{x} \\ $$$$\:\:\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{5}} }\:=\:−\mathrm{6}\left(−\Sigma\frac{\mathrm{1}}{{p}}+\Sigma\mathrm{2}−\Sigma{p}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{7}\Sigma\frac{\mathrm{1}}{{p}}−\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{13}\Sigma\frac{\mathrm{1}}{{p}}+\mathrm{6}\Sigma{p}−\mathrm{45} \\ $$$$\Sigma\frac{\mathrm{1}}{{p}^{\mathrm{5}} }\:=\:\mathrm{13}\left(\frac{{pq}+{qr}+{rp}}{{pqr}}\right)+\mathrm{6}\left({p}+{q}+{r}\right)−\mathrm{45} \\ $$$$\:{and}\:{since}\:\:{pq}+{qr}+{rp}\:=\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:{p}+{q}+{r}\:=\:\mathrm{2}\:;\:\:{pqr}\:=\:−\mathrm{1}\:,\:{So} \\ $$$$\:\:\:\:\Sigma\frac{\mathrm{1}}{\boldsymbol{{p}}^{\mathrm{5}} }\:=\:\mathrm{13}\left(−\mathrm{1}\right)+\mathrm{6}\left(\mathrm{2}\right)−\mathrm{45} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{46}\:. \\ $$$$ \\ $$

Commented by naka3546 last updated on 20/Oct/18

−46

$$−\mathrm{46} \\ $$

Commented by ajfour last updated on 20/Oct/18

yes, i corrected!

$${yes},\:{i}\:{corrected}! \\ $$

Answered by naka3546 last updated on 20/Oct/18

Commented by Tawa1 last updated on 20/Oct/18

The image is not clear sir

$$\mathrm{The}\:\mathrm{image}\:\mathrm{is}\:\mathrm{not}\:\mathrm{clear}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

Commented by tanmay.chaudhury50@gmail.com last updated on 20/Oct/18

Terms of Service

Privacy Policy

Contact: info@tinkutara.com