Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 45346 by Tawa1 last updated on 12/Oct/18

Commented by Meritguide1234 last updated on 12/Oct/18

this is my old post 45204

$${this}\:{is}\:{my}\:{old}\:{post}\:\mathrm{45204} \\ $$

Commented by Tawa1 last updated on 12/Oct/18

What is the solution

$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18

=Σ_(r=1) ^(99) ((√(10+(√r) ))/(√(10−(√r) ))) (√(10+(√(99)))) > (√(10+(√1))) >(√(10+(√1))) (√(10+(√(99)))) > (√(10+(√2))) >(√(10+(√1))) (√(10+(√(99)))) >(√(10+(√3) )) >(√(10+(√1))) ........... ........... adding them 99×(√(10+(√(99)))) >N_r >99×(√(11)) x=10+(√(99)) 2x=20+2×(√(11)) ×3 2x=((√(11)) +3)^2 x=(1/2)((√(11)) +3)^2 (√x) =((3+(√(11)))/(√2)) =((3/(√2))+(√((11)/2)) ) 99×((3/(√2))+(√((11)/2)) )>N_r >99(√(11)) it is logic based justification...microsoft Excell can give the answer of the problem (√(10−(√(99)))) <(√(10−(√1))) <(√(10−(√1))) (√(10−(√(99)))) <(√(10−(√2))) <(√(10−(√1))) (√(10−(√(99)))) <(√(10−(√3))) <(√(10−(√1))) ........ ........ add them 99×(√(10−(√(99)))) <D_r <99×3 99×((√((11)/2)) −(3/(√2)))<D_r <99×3

$$=\underset{{r}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\frac{\sqrt{\mathrm{10}+\sqrt{{r}}\:}}{\sqrt{\mathrm{10}−\sqrt{{r}}\:}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{10}+\sqrt{\mathrm{99}}}\:\:\:\:>\:\:\sqrt{\mathrm{10}+\sqrt{\mathrm{1}}}\:\:\:\:\:>\sqrt{\mathrm{10}+\sqrt{\mathrm{1}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{10}+\sqrt{\mathrm{99}}}\:\:\:\:>\:\:\sqrt{\mathrm{10}+\sqrt{\mathrm{2}}}\:\:\:\:>\sqrt{\mathrm{10}+\sqrt{\mathrm{1}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{10}+\sqrt{\mathrm{99}}}\:\:\:\:>\sqrt{\mathrm{10}+\sqrt{\mathrm{3}}\:}\:\:\:\:\:\:>\sqrt{\mathrm{10}+\sqrt{\mathrm{1}}} \\ $$$$\:\:\:........... \\ $$$$\:\:\:\:\:...........\:\:\:{adding}\:{them} \\ $$$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{99}×\sqrt{\mathrm{10}+\sqrt{\mathrm{99}}}\:\:\:>{N}_{{r}} \:\:\:>\mathrm{99}×\sqrt{\mathrm{11}}\: \\ $$$${x}=\mathrm{10}+\sqrt{\mathrm{99}}\: \\ $$$$\mathrm{2}{x}=\mathrm{20}+\mathrm{2}×\sqrt{\mathrm{11}}\:×\mathrm{3} \\ $$$$\mathrm{2}{x}=\left(\sqrt{\mathrm{11}}\:+\mathrm{3}\right)^{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{11}}\:\:+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\sqrt{{x}}\:=\frac{\mathrm{3}+\sqrt{\mathrm{11}}}{\sqrt{\mathrm{2}}}\:=\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}+\sqrt{\frac{\mathrm{11}}{\mathrm{2}}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{99}×\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}+\sqrt{\frac{\mathrm{11}}{\mathrm{2}}}\:\right)>{N}_{{r}} >\mathrm{99}\sqrt{\mathrm{11}}\: \\ $$$${it}\:{is}\:{logic}\:{based}\:{justification}...{microsoft}\: \\ $$$${Excell}\:{can}\:{give}\:{the}\:{answer}\:{of}\:{the}\:{problem} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{10}−\sqrt{\mathrm{99}}}\:\:<\sqrt{\mathrm{10}−\sqrt{\mathrm{1}}}\:\:<\sqrt{\mathrm{10}−\sqrt{\mathrm{1}}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{10}−\sqrt{\mathrm{99}}}\:\:<\sqrt{\mathrm{10}−\sqrt{\mathrm{2}}}\:\:<\sqrt{\mathrm{10}−\sqrt{\mathrm{1}}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{10}−\sqrt{\mathrm{99}}}\:\:<\sqrt{\mathrm{10}−\sqrt{\mathrm{3}}}\:\:\:<\sqrt{\mathrm{10}−\sqrt{\mathrm{1}}}\: \\ $$$$\:\:\:\:\:\:\:\:\:........ \\ $$$$\:\:\:\:\:\:\:\:........\:\:\:\:{add}\:{them}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{99}×\sqrt{\mathrm{10}−\sqrt{\mathrm{99}}}\:\:<{D}_{{r}} <\mathrm{99}×\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{99}×\left(\sqrt{\frac{\mathrm{11}}{\mathrm{2}}}\:−\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\right)<{D}_{{r}} <\mathrm{99}×\mathrm{3} \\ $$

Commented by Tawa1 last updated on 12/Oct/18

God bless you sir. What is the final answer.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}. \\ $$

Commented by Meritguide1234 last updated on 12/Oct/18

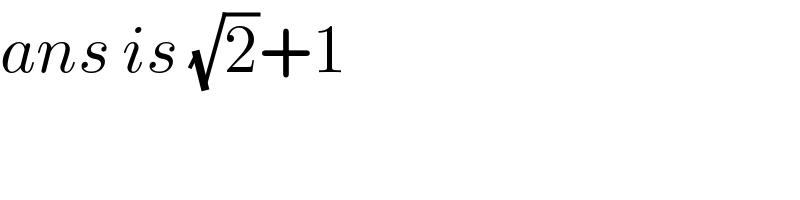
ans is (√2)+1

$${ans}\:{is}\:\sqrt{\mathrm{2}}+\mathrm{1} \\ $$

Commented by Meritguide1234 last updated on 12/Oct/18

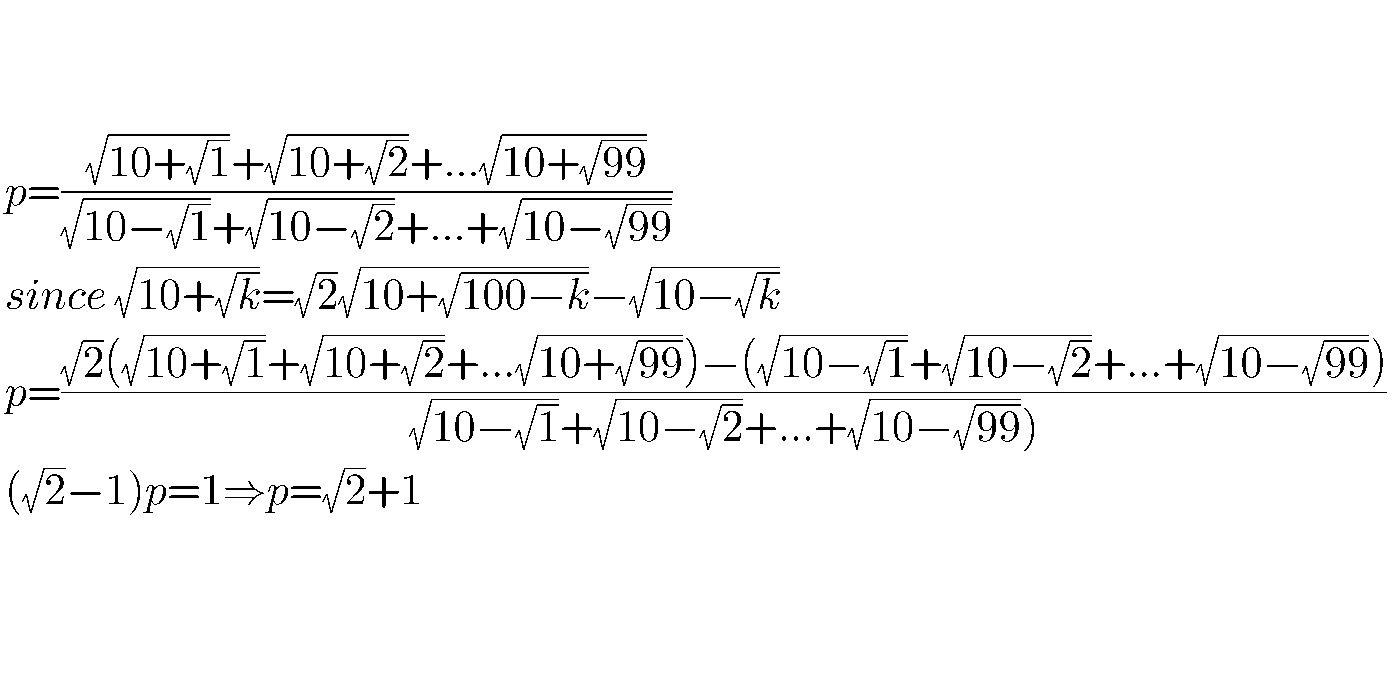
Commented by Tawa1 last updated on 12/Oct/18

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com