
Question Number 42422 by ajfour last updated on 25/Aug/18
Commented by ajfour last updated on 25/Aug/18
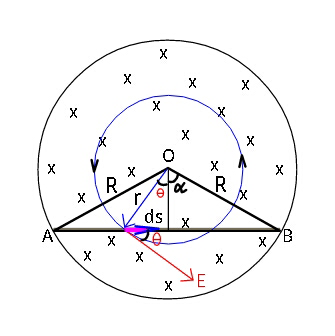
$${Q}.\mathrm{42278}\:\:{solution}\:\:\left({rishav}'{s}\:{question}\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Aug/18

$${pls}\:{explain}... \\ $$
Answered by ajfour last updated on 25/Aug/18

$${considering}\:{area}\:\bar {{A}}_{{OAB}} \:\:: \\ $$$$\frac{{d}\phi_{{B}} }{{dt}}=\:\frac{{l}}{\mathrm{2}}\frac{{dB}}{{dt}}\sqrt{{R}^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{\mathrm{4}}}\:=\:\oint_{{OAB}} \bar {{E}}.{d}\bar {{s}} \\ $$$$\Rightarrow\:\:\:\:\:\frac{{l}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{\mathrm{4}}}\:=\:\int_{{O}} ^{\:\:{A}} \bar {{E}}.{d}\bar {{s}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\int_{{A}} ^{\:\:{B}} \bar {{E}}.{d}\bar {{s}}\:+\int_{{B}} ^{\:\:{O}} \bar {{E}}.{d}\bar {{s}} \\ $$$$\Rightarrow\:\frac{{l}}{\mathrm{2}}\frac{{dB}}{{dt}}\sqrt{{R}^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{\mathrm{4}}}\:=\:\mathrm{0}+\left({V}_{{A}} −{V}_{{B}} \right)+\mathrm{0} \\ $$$${hence}\:{induced}\:{emf}\:{along}\:{rod}\:{ends} \\ $$$$\:\:\:\:{V}_{{A}} −{V}_{{B}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\frac{{dB}}{{dt}}\sqrt{{R}^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{\mathrm{4}}}\:. \\ $$$${Alternate}\:{method}\:: \\ $$$${Applying}\:{Faraday}'{s}\:{law}\:{around} \\ $$$${circle}\:{of}\:{radius}\:\boldsymbol{{r}}. \\ $$$$\oint\bar {{E}}.{d}\bar {{s}}\:=\:\frac{{d}\phi_{{B}} }{{dt}}\:=\:\pi{r}^{\mathrm{2}} \frac{{dB}}{{dt}} \\ $$$${E}\left(\mathrm{2}\pi{r}\right)=\pi{r}^{\mathrm{2}} \frac{{dB}}{{dt}} \\ $$$${E}\:=\:\frac{{r}}{\mathrm{2}}\frac{{dB}}{{dt}} \\ $$$${let}\:\bot\:{distance}\:{of}\:{rod}\:{from}\:{centre} \\ $$$${be}\:{h}\:. \\ $$$${Then}\:{along}\:{the}\:{rod} \\ $$$${V}_{{A}} +\int_{{A}} ^{\:\:{B}} \bar {{E}}.{d}\bar {{s}}\:={V}_{{B}} \\ $$$$\Rightarrow\:{V}_{{B}} −{V}_{{A}} =\frac{\mathrm{1}}{\mathrm{2}}\frac{{dB}}{{dt}}\int_{{A}} ^{\:\:{B}} \:{r}\left({ds}\right)\mathrm{cos}\:\theta \\ $$$$\:\:\:\:{V}_{{BA}} =\frac{\mathrm{1}}{\mathrm{2}}\frac{{dB}}{{dt}}\int_{−\alpha} ^{\:\:\alpha} \left({h}\mathrm{sec}\:\theta\right){ds}\left(\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\frac{{dB}}{{dt}}×{h}\int_{{A}} ^{\:\:{B}} {ds} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\frac{{dB}}{{dt}}×{hl} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{{l}}{\mathrm{2}}\frac{{dB}}{{dt}}\sqrt{{R}^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{\mathrm{4}}}\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Aug/18
$${excellent}...{bah}\:{darun}.. \\ $$
