
Previous in Relation and Functions Next in Relation and Functions
Question Number 42278 by rish@bh last updated on 21/Aug/18
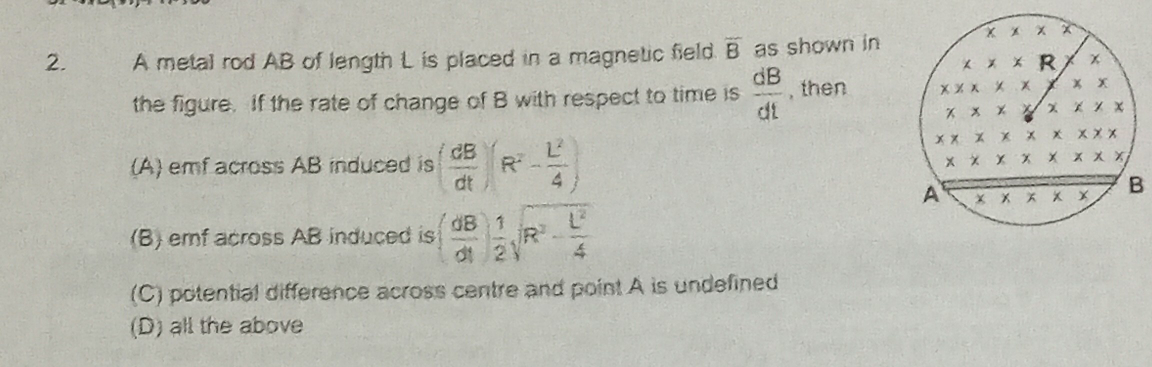
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Aug/18

$${excellent}\:{problem}... \\ $$$$\Psi=\overset{\rightarrow} {{B}}.\overset{\rightarrow} {{A}} \\ $$$$\frac{{d}\Psi}{{dt}}=\overset{\rightarrow} {{B}}.\frac{{d}\overset{\rightarrow} {{A}}}{{dt}}+\frac{{d}\overset{\rightarrow} {{B}}}{{dt}}.\overset{\rightarrow} {{A}}\:\:\:\:\:\:{B}={magnetic}\:{flux} \\ $$$$\overset{\rightarrow} {{A}}={area}\:{vector} \\ $$$${here}\frac{{d}\overset{\rightarrow} {{A}}}{{dt}}=\mathrm{0}{since}\:{no}\:{relative}\:{motion}\:{between}\:\overset{\rightarrow} {{B}} \\ $$$${and}\:{area}\:{vector}\:\overset{\rightarrow} {{A}} \\ $$$$ \\ $$$$\frac{{d}\Psi}{{dt}}=\frac{{dB}}{{dt}}.\overset{\rightarrow} {{A}} \\ $$$$−{e}=\frac{{d}\Psi}{{dt}}=\frac{{d}\overset{\rightarrow} {{B}}}{{dt}}.\overset{\rightarrow} {{A}} \\ $$$${now}\:{what}\:{is}\:{the}\:{value}\:{of}\:\overset{\rightarrow} {{A}} \\ $$$${let}\:{me}\:{think}...{wait}... \\ $$
