Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 41160 by behi83417@gmail.com last updated on 02/Aug/18

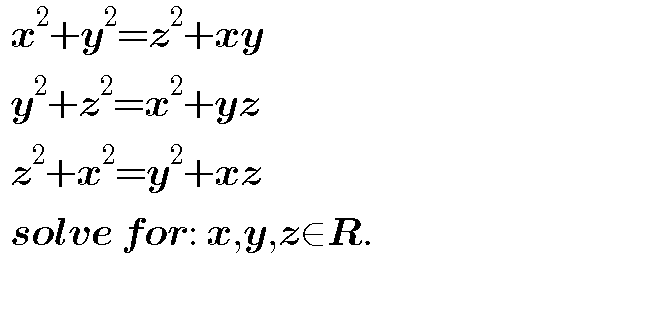
Commented by behi83417@gmail.com last updated on 02/Aug/18

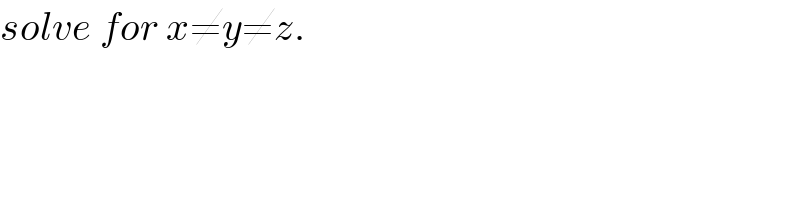
solve for x≠y≠z.

$${solve}\:{for}\:{x}\neq{y}\neq{z}. \\ $$

Commented by MJS last updated on 02/Aug/18

you know any solution? I don′t think there is one but I could be wrong

$$\mathrm{you}\:\mathrm{know}\:\mathrm{any}\:\mathrm{solution}? \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{there}\:\mathrm{is}\:\mathrm{one}\:\mathrm{but}\:\mathrm{I}\:\mathrm{could}\:\mathrm{be}\:\mathrm{wrong} \\ $$

Commented by MJS last updated on 02/Aug/18

(1) z=±(√(−x^2 +xy−y^2 )) (2) z=(y/2)±((√(4x^2 −3y^2 ))/2) (3) z=(x/2)±((√(−3x^2 +4y^2 ))/2) we have to solve ±(√(−x^2 +xy−y^2 ))=(y/2)±((√(4x^2 −3y^2 ))/2) ±(√(−x^2 +xy−y^2 ))=(x/2)±((√(−3x^2 +4y^2 ))/2) (y/2)±((√(4x^2 −3y^2 ))/2)=(x/2)±((√(−3x^2 +4y^2 ))/2) each line represents 4 equations but all of them have got the only solution x=y ⇒ ⇒ x=y=z

$$\left(\mathrm{1}\right)\:{z}=\pm\sqrt{−{x}^{\mathrm{2}} +{xy}−{y}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}\right)\:{z}=\frac{{y}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:{z}=\frac{{x}}{\mathrm{2}}\pm\frac{\sqrt{−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\pm\sqrt{−{x}^{\mathrm{2}} +{xy}−{y}^{\mathrm{2}} }=\frac{{y}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\pm\sqrt{−{x}^{\mathrm{2}} +{xy}−{y}^{\mathrm{2}} }=\frac{{x}}{\mathrm{2}}\pm\frac{\sqrt{−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\frac{{y}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} }}{\mathrm{2}}=\frac{{x}}{\mathrm{2}}\pm\frac{\sqrt{−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\mathrm{each}\:\mathrm{line}\:\mathrm{represents}\:\mathrm{4}\:\mathrm{equations}\:\mathrm{but}\:\mathrm{all}\:\mathrm{of} \\ $$$$\mathrm{them}\:\mathrm{have}\:\mathrm{got}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:{x}={y}\:\Rightarrow \\ $$$$\Rightarrow\:{x}={y}={z} \\ $$

Answered by MJS last updated on 02/Aug/18

x=y=z maybe more... ...no.

$${x}={y}={z} \\ $$$$\mathrm{maybe}\:\mathrm{more}... \\ $$$$...\mathrm{no}. \\ $$

Commented by rahul 19 last updated on 02/Aug/18

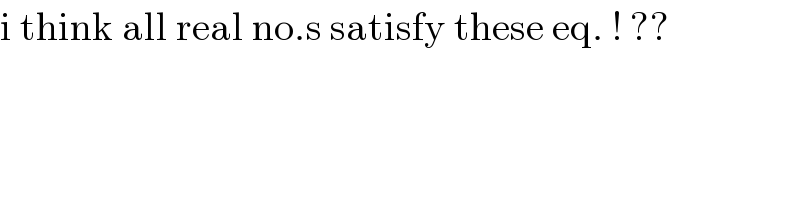
i think all real no.s satisfy these eq. ! ??

$$\mathrm{i}\:\mathrm{think}\:\mathrm{all}\:\mathrm{real}\:\mathrm{no}.\mathrm{s}\:\mathrm{satisfy}\:\mathrm{these}\:\mathrm{eq}.\:!\:?? \\ $$

Commented by MJS last updated on 02/Aug/18

yes

$$\mathrm{yes} \\ $$

Answered by rahul 19 last updated on 02/Aug/18

x=y=z=k where k ε R.

$${x}={y}={z}={k} \\ $$$${where}\:{k}\:\epsilon\:\mathrm{R}. \\ $$

Answered by behi83417@gmail.com last updated on 02/Aug/18

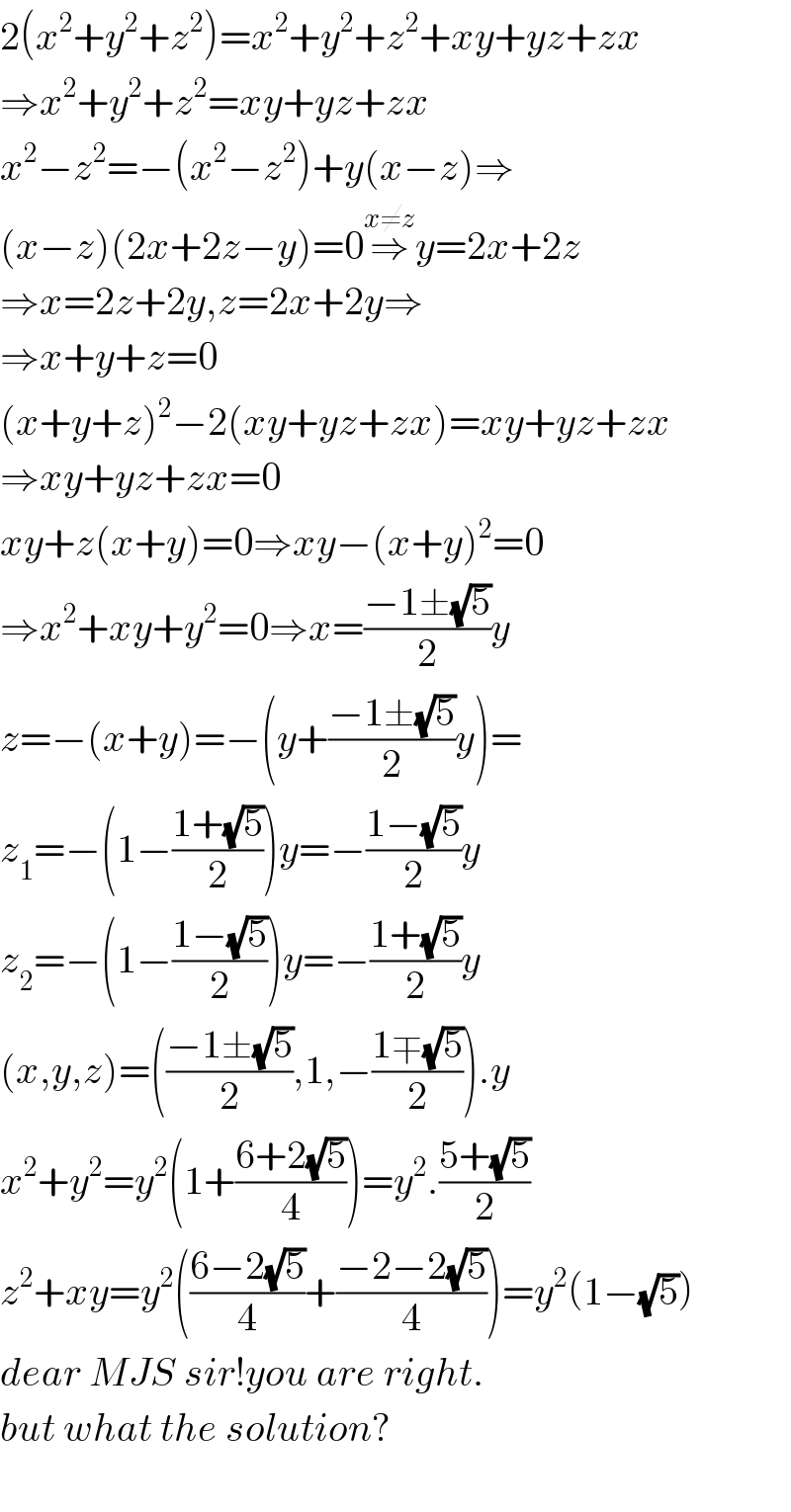
2(x^2 +y^2 +z^2 )=x^2 +y^2 +z^2 +xy+yz+zx ⇒x^2 +y^2 +z^2 =xy+yz+zx x^2 −z^2 =−(x^2 −z^2 )+y(x−z)⇒ (x−z)(2x+2z−y)=0⇒^(x≠z) y=2x+2z ⇒x=2z+2y,z=2x+2y⇒ ⇒x+y+z=0 (x+y+z)^2 −2(xy+yz+zx)=xy+yz+zx ⇒xy+yz+zx=0 xy+z(x+y)=0⇒xy−(x+y)^2 =0 ⇒x^2 +xy+y^2 =0⇒x=((−1±(√5))/2)y z=−(x+y)=−(y+((−1±(√5))/2)y)= z_1 =−(1−((1+(√5))/2))y=−((1−(√5))/2)y z_2 =−(1−((1−(√5))/2))y=−((1+(√5))/2)y (x,y,z)=(((−1±(√5))/2),1,−((1∓(√5))/2)).y x^2 +y^2 =y^2 (1+((6+2(√5))/4))=y^2 .((5+(√5))/2) z^2 +xy=y^2 (((6−2(√5))/4)+((−2−2(√5))/4))=y^2 (1−(√5)) dear MJS sir!you are right. but what the solution?

$$\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{xy}+{yz}+{zx} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={xy}+{yz}+{zx} \\ $$$${x}^{\mathrm{2}} −{z}^{\mathrm{2}} =−\left({x}^{\mathrm{2}} −{z}^{\mathrm{2}} \right)+{y}\left({x}−{z}\right)\Rightarrow \\ $$$$\left({x}−{z}\right)\left(\mathrm{2}{x}+\mathrm{2}{z}−{y}\right)=\mathrm{0}\overset{{x}\neq{z}} {\Rightarrow}{y}=\mathrm{2}{x}+\mathrm{2}{z} \\ $$$$\Rightarrow{x}=\mathrm{2}{z}+\mathrm{2}{y},{z}=\mathrm{2}{x}+\mathrm{2}{y}\Rightarrow \\ $$$$\Rightarrow{x}+{y}+{z}=\mathrm{0} \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{2}} −\mathrm{2}\left({xy}+{yz}+{zx}\right)={xy}+{yz}+{zx} \\ $$$$\Rightarrow{xy}+{yz}+{zx}=\mathrm{0} \\ $$$${xy}+{z}\left({x}+{y}\right)=\mathrm{0}\Rightarrow{xy}−\left({x}+{y}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}{y} \\ $$$${z}=−\left({x}+{y}\right)=−\left({y}+\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}{y}\right)= \\ $$$${z}_{\mathrm{1}} =−\left(\mathrm{1}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right){y}=−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{y} \\ $$$${z}_{\mathrm{2}} =−\left(\mathrm{1}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right){y}=−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{y} \\ $$$$\left({x},{y},{z}\right)=\left(\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}},\mathrm{1},−\frac{\mathrm{1}\mp\sqrt{\mathrm{5}}}{\mathrm{2}}\right).{y} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={y}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}\right)={y}^{\mathrm{2}} .\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} +{xy}={y}^{\mathrm{2}} \left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}+\frac{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}\right)={y}^{\mathrm{2}} \left(\mathrm{1}−\sqrt{\mathrm{5}}\right) \\ $$$${dear}\:{MJS}\:{sir}!{you}\:{are}\:{right}. \\ $$$${but}\:{what}\:{the}\:{solution}? \\ $$$$ \\ $$

Commented by MJS last updated on 02/Aug/18

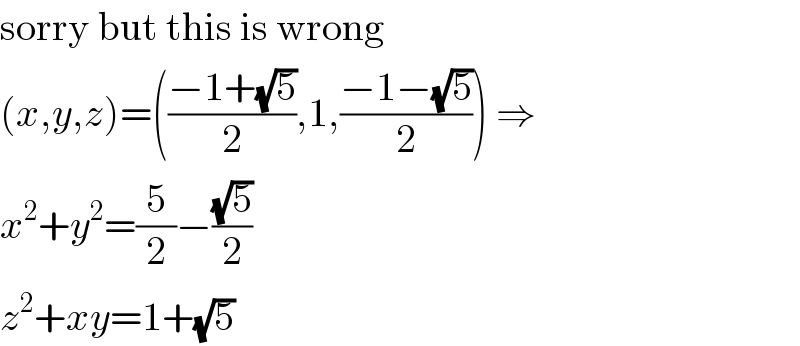
sorry but this is wrong (x,y,z)=(((−1+(√5))/2),1,((−1−(√5))/2)) ⇒ x^2 +y^2 =(5/2)−((√5)/2) z^2 +xy=1+(√5)

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\left({x},{y},{z}\right)=\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\mathrm{1},\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} +{xy}=\mathrm{1}+\sqrt{\mathrm{5}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com