
Question Number 40952 by Raj Singh last updated on 30/Jul/18
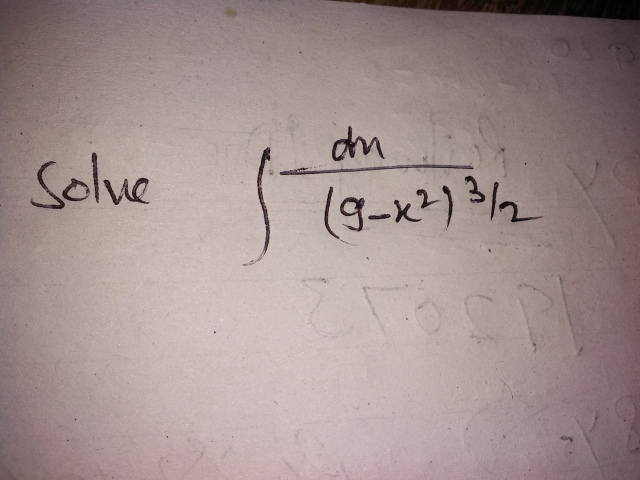
Commented by abdo mathsup 649 cc last updated on 30/Jul/18
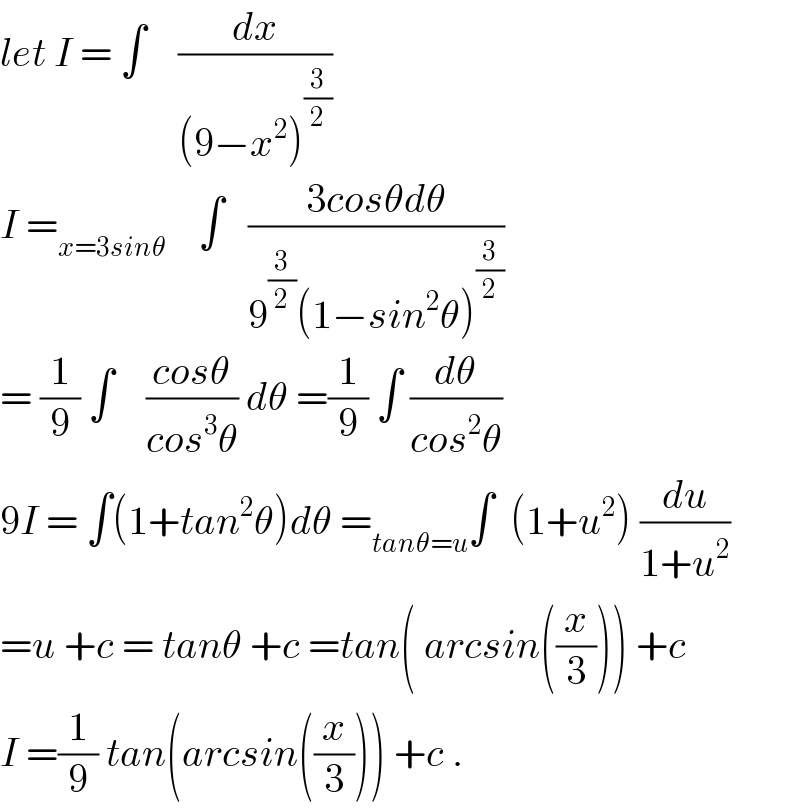
$${let}\:{I}\:=\:\int\:\:\:\:\frac{{dx}}{\left(\mathrm{9}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${I}\:=_{{x}=\mathrm{3}{sin}\theta} \:\:\:\:\int\:\:\:\frac{\mathrm{3}{cos}\theta{d}\theta}{\mathrm{9}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}−{sin}^{\mathrm{2}} \theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{9}}\:\int\:\:\:\:\frac{{cos}\theta}{{cos}^{\mathrm{3}} \theta}\:{d}\theta\:=\frac{\mathrm{1}}{\mathrm{9}}\:\int\:\frac{{d}\theta}{{cos}^{\mathrm{2}} \theta} \\ $$$$\mathrm{9}{I}\:=\:\int\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta\:=_{{tan}\theta={u}} \int\:\:\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$={u}\:+{c}\:=\:{tan}\theta\:+{c}\:={tan}\left(\:{arcsin}\left(\frac{{x}}{\mathrm{3}}\right)\right)\:+{c} \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{9}}\:{tan}\left({arcsin}\left(\frac{{x}}{\mathrm{3}}\right)\right)\:+{c}\:. \\ $$
