
Question Number 40306 by behi83417@gmail.com last updated on 19/Jul/18
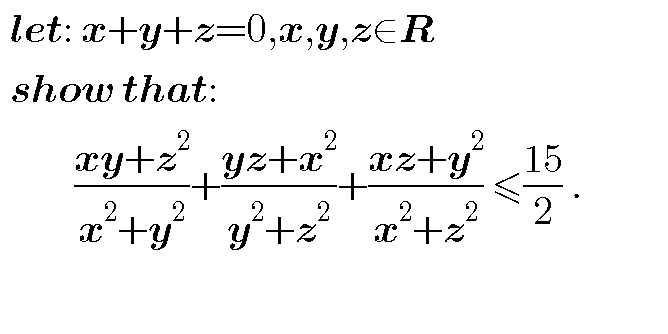
Commented by MJS last updated on 20/Jul/18
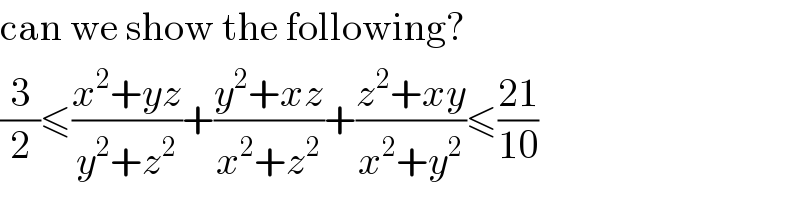
$$\mathrm{can}\:\mathrm{we}\:\mathrm{show}\:\mathrm{the}\:\mathrm{following}? \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\leqslant\frac{{x}^{\mathrm{2}} +{yz}}{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} +{xz}}{{x}^{\mathrm{2}} +{z}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} +{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{21}}{\mathrm{10}} \\ $$
Commented by MJS last updated on 20/Jul/18
![f(x,y,z)=((x^2 +yz)/(y^2 +z^2 ))+((y^2 +xz)/(x^2 +z^2 ))+((z^2 +xy)/(x^2 +y^2 )) z=−(x+y) f(x,y,−(x+y))= =g(x,y)=((3(x^6 +y^6 +3xy(x^4 +y^4 )+8x^2 y^2 (x^2 +y^2 )+11x^3 y^3 ))/((x^2 +y^2 )((x+y)^2 +x^2 )((x+y)^2 +y^2 ))) (d/dx)[g(x,y)]=−((15xy^2 (2(x^8 −y^8 )+9xy(x^6 −y^6 )+16x^2 y^2 (x^4 −y^4 )+14x^3 y^3 (x^2 −y^2 )))/((x^2 +y^2 )^2 ((x+_ y)^2 +x^2 )^2 ((x+y)^2 +y^2 )^2 )) (d/dx)[g(x,y)]=0 ⇒ x=0 ∨ y=0 ∨ 2(x^8 −y^8 )+9xy(x^6 −y^6 )+16x^2 y^2 (x^4 −y^4 )+14x^3 y^3 (x^2 −y^2 )=0 x={−2y; −y; −(y/2); 0; y; −(y/2)(1+i(√3)); −(y/2)(1−i(√3))} f(x, y, z)={((21)/(10)); (3/2); ((21)/(10)); (3/2); ((21)/(10)); −6; −6} so these are the minima and maxima of f(x, y, z)](Q40359.png)
$${f}\left({x},{y},{z}\right)=\frac{{x}^{\mathrm{2}} +{yz}}{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} +{xz}}{{x}^{\mathrm{2}} +{z}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} +{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${z}=−\left({x}+{y}\right) \\ $$$${f}\left({x},{y},−\left({x}+{y}\right)\right)= \\ $$$$={g}\left({x},{y}\right)=\frac{\mathrm{3}\left({x}^{\mathrm{6}} +{y}^{\mathrm{6}} +\mathrm{3}{xy}\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} \right)+\mathrm{8}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+\mathrm{11}{x}^{\mathrm{3}} {y}^{\mathrm{3}} \right)}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left(\left({x}+{y}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} \right)\left(\left({x}+{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} \\ $$$$\frac{{d}}{{dx}}\left[{g}\left({x},{y}\right)\right]=−\frac{\mathrm{15}{xy}^{\mathrm{2}} \left(\mathrm{2}\left({x}^{\mathrm{8}} −{y}^{\mathrm{8}} \right)+\mathrm{9}{xy}\left({x}^{\mathrm{6}} −{y}^{\mathrm{6}} \right)+\mathrm{16}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{4}} −{y}^{\mathrm{4}} \right)+\mathrm{14}{x}^{\mathrm{3}} {y}^{\mathrm{3}} \left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\right)}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\left({x}+_{} {y}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\left({x}+{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\frac{{d}}{{dx}}\left[{g}\left({x},{y}\right)\right]=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{0}\:\vee\:{y}=\mathrm{0}\:\vee \\ $$$$\mathrm{2}\left({x}^{\mathrm{8}} −{y}^{\mathrm{8}} \right)+\mathrm{9}{xy}\left({x}^{\mathrm{6}} −{y}^{\mathrm{6}} \right)+\mathrm{16}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{4}} −{y}^{\mathrm{4}} \right)+\mathrm{14}{x}^{\mathrm{3}} {y}^{\mathrm{3}} \left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${x}=\left\{−\mathrm{2}{y};\:−{y};\:−\frac{{y}}{\mathrm{2}};\:\mathrm{0};\:{y};\:−\frac{{y}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}\right);\:−\frac{{y}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}\right)\right\} \\ $$$${f}\left({x},\:{y},\:{z}\right)=\left\{\frac{\mathrm{21}}{\mathrm{10}};\:\frac{\mathrm{3}}{\mathrm{2}};\:\frac{\mathrm{21}}{\mathrm{10}};\:\frac{\mathrm{3}}{\mathrm{2}};\:\frac{\mathrm{21}}{\mathrm{10}};\:−\mathrm{6};\:−\mathrm{6}\right\} \\ $$$$\mathrm{so}\:\mathrm{these}\:\mathrm{are}\:\mathrm{the}\:\mathrm{minima}\:\mathrm{and}\:\mathrm{maxima}\:\mathrm{of}\:{f}\left({x},\:{y},\:{z}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jul/18
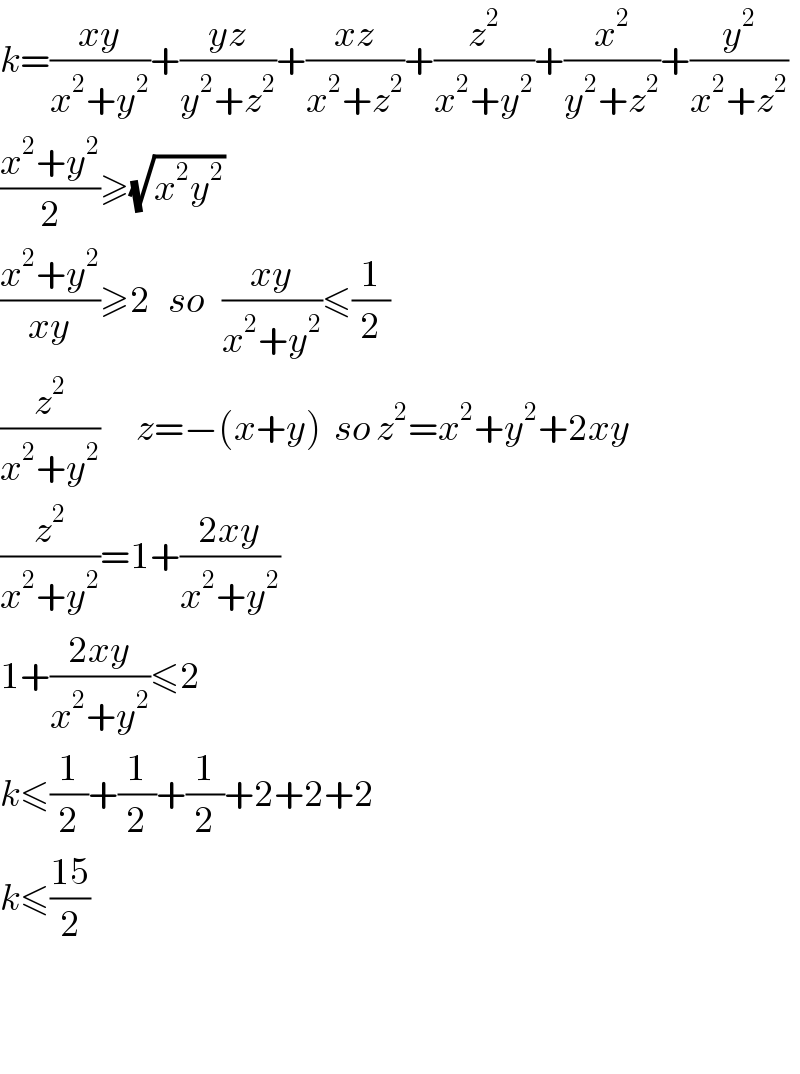
$${k}=\frac{{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+\frac{{yz}}{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }+\frac{{xz}}{{x}^{\mathrm{2}} +{z}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{z}^{\mathrm{2}} } \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}\geqslant\sqrt{{x}^{\mathrm{2}} {y}^{\mathrm{2}} } \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{xy}}\geqslant\mathrm{2}\:\:\:{so}\:\:\:\frac{{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:\:\:\:\:{z}=−\left({x}+{y}\right)\:\:{so}\:{z}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy} \\ $$$$\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\mathrm{1}+\frac{\mathrm{2}{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\mathrm{1}+\frac{\mathrm{2}{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\mathrm{2} \\ $$$${k}\leqslant\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}+\mathrm{2}+\mathrm{2} \\ $$$${k}\leqslant\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Answered by math1967 last updated on 19/Jul/18
![x,y,z∈R ∴(x−y)^2 ≥0 (y−z)^2 ≥0,(z−x)^2 ≥0 ∴x^2 +y^2 ≥2xy .......1 From 1 (1/(x^2 +y^2 ))≤(1/(2xy)) ((xy)/(x^2 +y^2 ))≤(1/2) ......(2) Again x+y+z=0 ⇒x^2 +y^2 +2xy=z^2 ∴x^2 +y^2 +3xy=xy+z^2 From (2) ((3xy)/(x^2 +y^2 ))≤(3/2) 1+((3xy)/(x^2 +y^2 ))≤(5/2) ((x^2 +y^2 +3xy)/(x^2 +y^2 ))≤(5/2) ((xy+z^2 )/(x^2 +y^2 ))≤(5/2) [x^2 +y^2 +3xy=xy+z^2 ] similarly ((yz+x^2 )/(y^2 +z^2 ))≤(5/2) ((zx+y^2 )/(z^2 +x^2 ))≤(5/2) ∴((xy+z^2 )/(x^2 +y^2 )) +((yz+x^2 )/(y^2 +z^2 )) +((zx+y^2 )/(z^2 +x^2 ))≤((15)/2)](Q40312.png)
$${x},{y},{z}\in{R}\:\:\therefore\left({x}−{y}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\left({y}−{z}\right)^{\mathrm{2}} \geqslant\mathrm{0},\left({z}−{x}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\therefore{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \geqslant\mathrm{2}{xy}\:.......\mathrm{1} \\ $$$${From}\:\mathrm{1}\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{2}{xy}}\:\:\: \\ $$$$\:\:\:\frac{{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:......\left(\mathrm{2}\right) \\ $$$$ \\ $$$${Again}\:{x}+{y}+{z}=\mathrm{0} \\ $$$$\:\:\:\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy}={z}^{\mathrm{2}} \\ $$$$\therefore{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{xy}={xy}+{z}^{\mathrm{2}} \: \\ $$$${From}\:\left(\mathrm{2}\right)\:\frac{\mathrm{3}{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\mathrm{1}+\frac{\mathrm{3}{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\frac{{xy}+{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{5}}{\mathrm{2}}\:\:\:\:\left[{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{xy}={xy}+{z}^{\mathrm{2}} \right] \\ $$$${similarly}\:\frac{{yz}+{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }\leqslant\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\frac{{zx}+{y}^{\mathrm{2}} }{{z}^{\mathrm{2}} +{x}^{\mathrm{2}} }\leqslant\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\therefore\frac{{xy}+{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:+\frac{{yz}+{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }\:+\frac{{zx}+{y}^{\mathrm{2}} }{{z}^{\mathrm{2}} +{x}^{\mathrm{2}} }\leqslant\frac{\mathrm{15}}{\mathrm{2}} \\ $$$$ \\ $$
