
Question Number 39174 by jasno91 last updated on 03/Jul/18

Answered by MrW3 last updated on 03/Jul/18
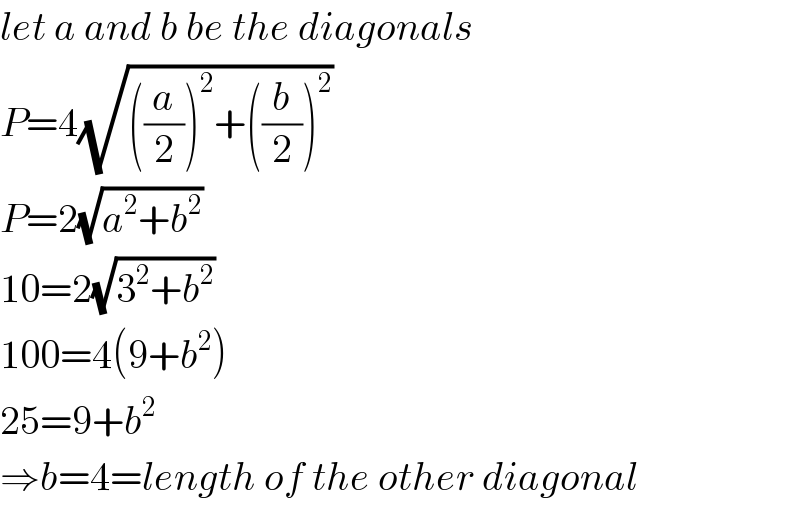
$${let}\:{a}\:{and}\:{b}\:{be}\:{the}\:{diagonals} \\ $$$${P}=\mathrm{4}\sqrt{\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${P}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\mathrm{10}=\mathrm{2}\sqrt{\mathrm{3}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\mathrm{100}=\mathrm{4}\left(\mathrm{9}+{b}^{\mathrm{2}} \right) \\ $$$$\mathrm{25}=\mathrm{9}+{b}^{\mathrm{2}} \\ $$$$\Rightarrow{b}=\mathrm{4}={length}\:{of}\:{the}\:{other}\:{diagonal} \\ $$
