
Question Number 36855 by Tinkutara last updated on 06/Jun/18

Commented by Tinkutara last updated on 06/Jun/18

Answered by ajfour last updated on 11/Jun/18

$$\frac{\tau_{{A}} }{\tau_{{B}} }\:=\:\frac{\mathrm{6}}{\sqrt{\mathrm{11}}}\:. \\ $$
Commented by Tinkutara last updated on 11/Jun/18
How?
Commented by ajfour last updated on 11/Jun/18
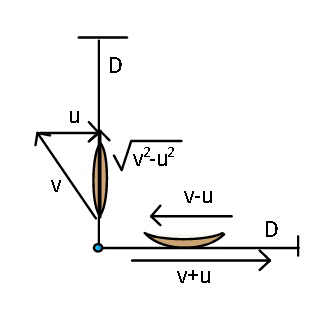
Commented by ajfour last updated on 11/Jun/18
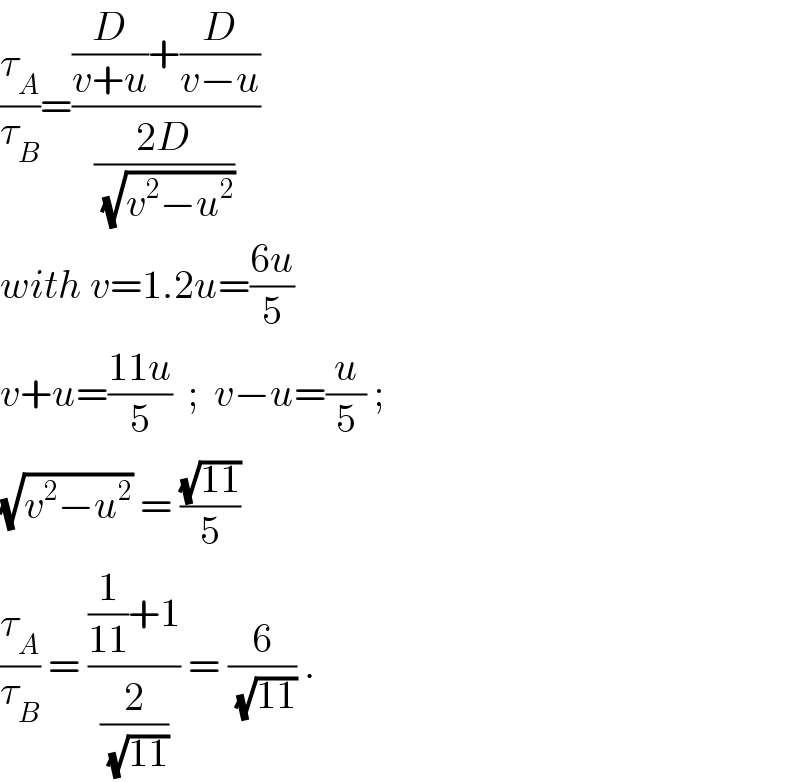
$$\frac{\tau_{{A}} }{\tau_{{B}} }=\frac{\frac{{D}}{{v}+{u}}+\frac{{D}}{{v}−{u}}}{\frac{\mathrm{2}{D}}{\sqrt{{v}^{\mathrm{2}} −{u}^{\mathrm{2}} }}}\: \\ $$$${with}\:{v}=\mathrm{1}.\mathrm{2}{u}=\frac{\mathrm{6}{u}}{\mathrm{5}} \\ $$$${v}+{u}=\frac{\mathrm{11}{u}}{\mathrm{5}}\:\:;\:\:{v}−{u}=\frac{{u}}{\mathrm{5}}\:;\: \\ $$$$\sqrt{{v}^{\mathrm{2}} −{u}^{\mathrm{2}} }\:=\:\frac{\sqrt{\mathrm{11}}}{\mathrm{5}} \\ $$$$\frac{\tau_{{A}} }{\tau_{{B}} }\:=\:\frac{\frac{\mathrm{1}}{\mathrm{11}}+\mathrm{1}}{\frac{\mathrm{2}}{\sqrt{\mathrm{11}}}}\:=\:\frac{\mathrm{6}}{\sqrt{\mathrm{11}}}\:. \\ $$
Commented by Tinkutara last updated on 14/Jun/18
Thanks Sir!
