
Question Number 33452 by ajfour last updated on 16/Apr/18
Commented by ajfour last updated on 16/Apr/18

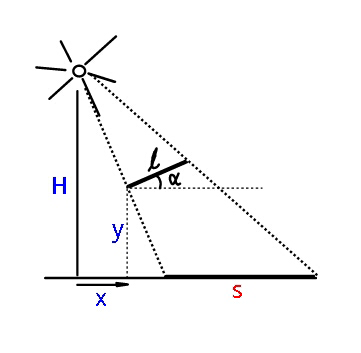
$${Find}\:{length}\:{of}\:{shadow}\:{s}\:{of}\:{a}\: \\ $$$${stick}\:{of}\:{length}\:\boldsymbol{{l}}\:{when}\:{source} \\ $$$${of}\:{light}\:{is}\:{a}\:{point}\:{source}\:{at} \\ $$$${height}\:{H}\:{above}\:{ground}. \\ $$
Commented by ajfour last updated on 19/Apr/18
$${question}\:{for}\:{you},\:{mrW}\:{Sir}... \\ $$$$ \\ $$
Answered by MrW3 last updated on 12/Jun/18
Commented by MrW3 last updated on 12/Jun/18
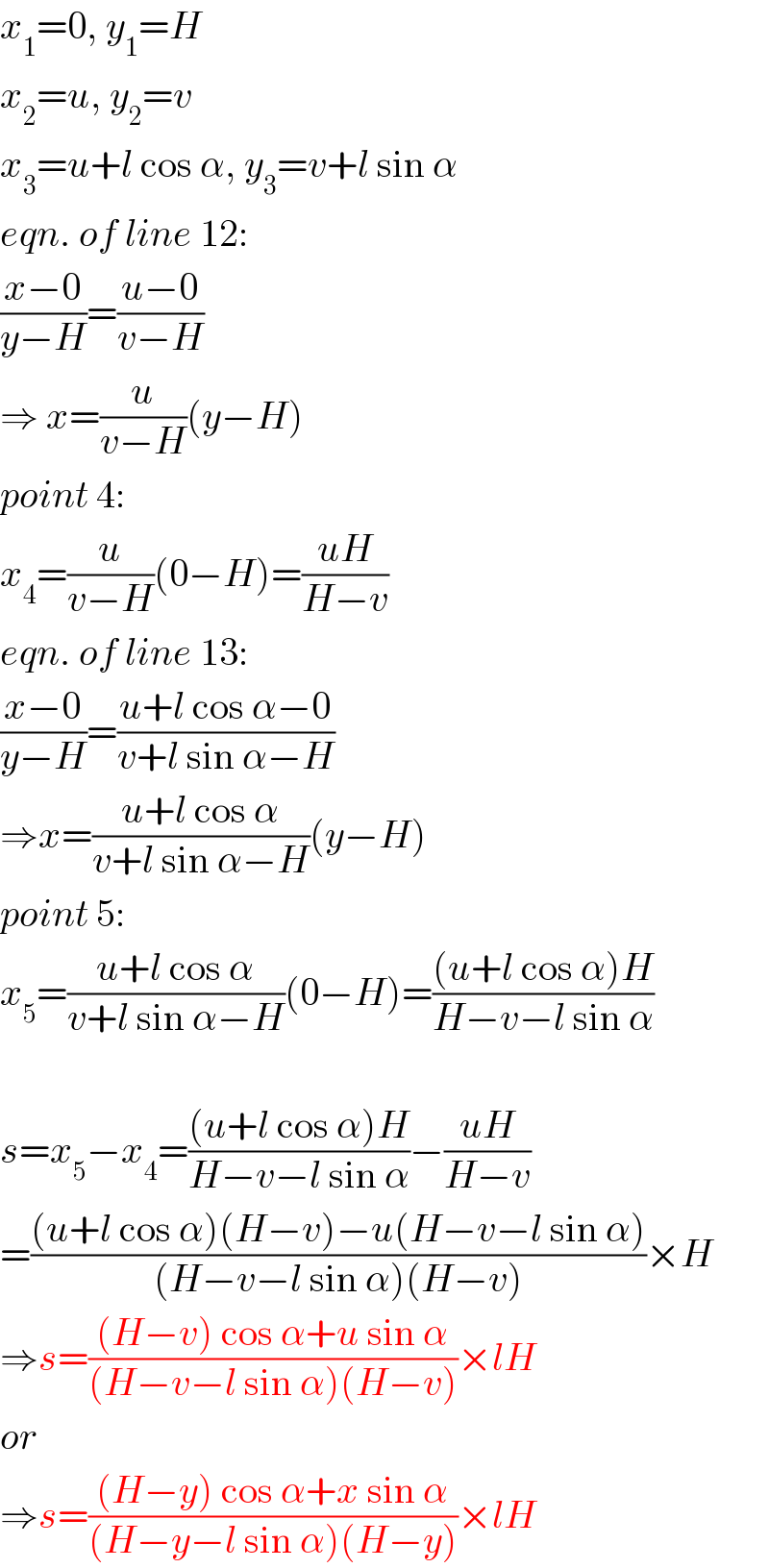
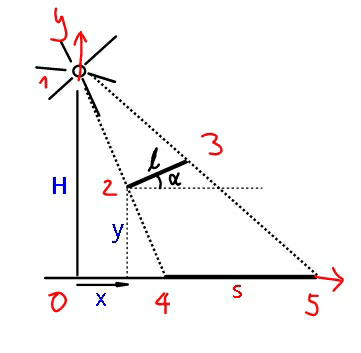
$${x}_{\mathrm{1}} =\mathrm{0},\:{y}_{\mathrm{1}} ={H} \\ $$$${x}_{\mathrm{2}} ={u},\:{y}_{\mathrm{2}} ={v} \\ $$$${x}_{\mathrm{3}} ={u}+{l}\:\mathrm{cos}\:\alpha,\:{y}_{\mathrm{3}} ={v}+{l}\:\mathrm{sin}\:\alpha \\ $$$${eqn}.\:{of}\:{line}\:\mathrm{12}: \\ $$$$\frac{{x}−\mathrm{0}}{{y}−{H}}=\frac{{u}−\mathrm{0}}{{v}−{H}} \\ $$$$\Rightarrow\:{x}=\frac{{u}}{{v}−{H}}\left({y}−{H}\right) \\ $$$${point}\:\mathrm{4}: \\ $$$${x}_{\mathrm{4}} =\frac{{u}}{{v}−{H}}\left(\mathrm{0}−{H}\right)=\frac{{uH}}{{H}−{v}} \\ $$$${eqn}.\:{of}\:{line}\:\mathrm{13}: \\ $$$$\frac{{x}−\mathrm{0}}{{y}−{H}}=\frac{{u}+{l}\:\mathrm{cos}\:\alpha−\mathrm{0}}{{v}+{l}\:\mathrm{sin}\:\alpha−{H}} \\ $$$$\Rightarrow{x}=\frac{{u}+{l}\:\mathrm{cos}\:\alpha}{{v}+{l}\:\mathrm{sin}\:\alpha−{H}}\left({y}−{H}\right) \\ $$$${point}\:\mathrm{5}: \\ $$$${x}_{\mathrm{5}} =\frac{{u}+{l}\:\mathrm{cos}\:\alpha}{{v}+{l}\:\mathrm{sin}\:\alpha−{H}}\left(\mathrm{0}−{H}\right)=\frac{\left({u}+{l}\:\mathrm{cos}\:\alpha\right){H}}{{H}−{v}−{l}\:\mathrm{sin}\:\alpha} \\ $$$$ \\ $$$${s}={x}_{\mathrm{5}} −{x}_{\mathrm{4}} =\frac{\left({u}+{l}\:\mathrm{cos}\:\alpha\right){H}}{{H}−{v}−{l}\:\mathrm{sin}\:\alpha}−\frac{{uH}}{{H}−{v}} \\ $$$$=\frac{\left({u}+{l}\:\mathrm{cos}\:\alpha\right)\left({H}−{v}\right)−{u}\left({H}−{v}−{l}\:\mathrm{sin}\:\alpha\right)}{\left({H}−{v}−{l}\:\mathrm{sin}\:\alpha\right)\left({H}−{v}\right)}×{H} \\ $$$$\Rightarrow{s}=\frac{\left({H}−{v}\right)\:\mathrm{cos}\:\alpha+{u}\:\mathrm{sin}\:\alpha}{\left({H}−{v}−{l}\:\mathrm{sin}\:\alpha\right)\left({H}−{v}\right)}×{lH} \\ $$$${or} \\ $$$$\Rightarrow{s}=\frac{\left({H}−{y}\right)\:\mathrm{cos}\:\alpha+{x}\:\mathrm{sin}\:\alpha}{\left({H}−{y}−{l}\:\mathrm{sin}\:\alpha\right)\left({H}−{y}\right)}×{lH} \\ $$
