
Question Number 33239 by Tinkutara last updated on 13/Apr/18

Answered by ajfour last updated on 14/Apr/18
![2[mucos ((α/2))]=(2m)((u/2)) ⇒ cos ((α/2))=(1/2) ⇒ α = 120° .](Q33324.png)
$$\mathrm{2}\left[{mu}\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\right]=\left(\mathrm{2}{m}\right)\left(\frac{{u}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\Rightarrow\:\:\alpha\:=\:\mathrm{120}°\:. \\ $$
Commented by Tinkutara last updated on 15/Apr/18
But why after collision particles will stick together? Because components of velocities normal to Line of Impact will remain unchanged.
Commented by ajfour last updated on 15/Apr/18
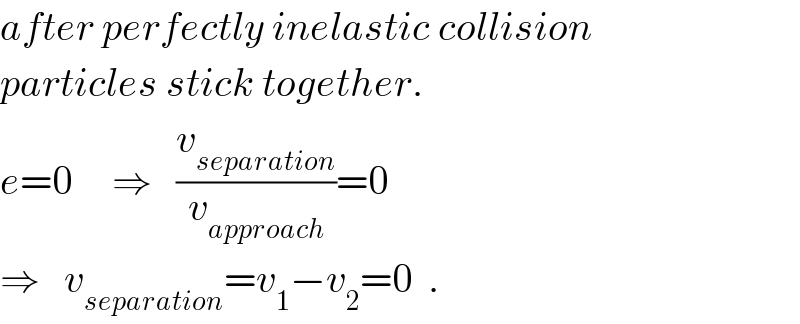
$${after}\:{perfectly}\:{inelastic}\:{collision} \\ $$$${particles}\:{stick}\:{together}. \\ $$$${e}=\mathrm{0}\:\:\:\:\:\Rightarrow\:\:\:\frac{{v}_{{separation}} }{{v}_{{approach}} }=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{v}_{{separation}} ={v}_{\mathrm{1}} −{v}_{\mathrm{2}} =\mathrm{0}\:\:. \\ $$
Commented by Tinkutara last updated on 15/Apr/18
But isn't that only in 1D and not in 2D?
Commented by ajfour last updated on 15/Apr/18

$${in}\:\:\mathrm{3}{D}\:\:{as}\:{well}. \\ $$
Commented by Tinkutara last updated on 15/Apr/18
Thank you very much Sir! I got the answer. ��������
