Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 31596 by Nayon.Sm last updated on 11/Mar/18

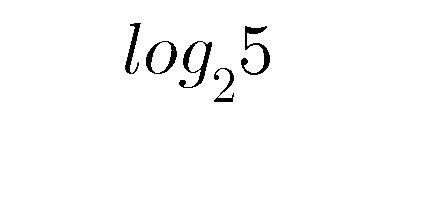
Commented by Nayon.Sm last updated on 11/Mar/18

Proof that it is irrational

Commented by rahul 19 last updated on 11/Mar/18

such type of questions are easily done by contradiction !

$${such}\:{type}\:{of}\:{questions}\:{are}\:{easily}\:{done}\: \\ $$$${by}\:{contradiction}\:! \\ $$

Answered by Joel578 last updated on 11/Mar/18

If log_2 5 is rational, then there is number a and b satisfy log_2 5 = (a/b), where a, b ∈ Z, b ≠ 0 log_2 5 = (a/b) → 2^(a/b) = 5 → 2^a = 5^b There is no number that satisfy the equation because LHS always even and RHS always odd Hence, log_2 5 is irrational

$$\mathrm{If}\:\:\mathrm{log}_{\mathrm{2}} \:\mathrm{5}\:\mathrm{is}\:\mathrm{rational},\:\mathrm{then}\:\mathrm{there}\:\mathrm{is}\:\mathrm{number}\:{a}\:\mathrm{and}\:{b} \\ $$$$\mathrm{satisfy}\:\mathrm{log}_{\mathrm{2}} \:\mathrm{5}\:=\:\frac{{a}}{{b}},\:\mathrm{where}\:{a},\:{b}\:\in\:\mathbb{Z},\:{b}\:\neq\:\mathrm{0} \\ $$$$\mathrm{log}_{\mathrm{2}} \:\mathrm{5}\:=\:\frac{\mathrm{a}}{\mathrm{b}}\:\:\rightarrow\:\:\mathrm{2}^{\frac{{a}}{{b}}} \:=\:\mathrm{5}\:\:\rightarrow\:\:\mathrm{2}^{{a}} \:=\:\mathrm{5}^{{b}} \\ $$$$\mathrm{There}\:\mathrm{is}\:\mathrm{no}\:\mathrm{number}\:\mathrm{that}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{because}\:\mathrm{LHS}\:\mathrm{always}\:\mathrm{even}\:\mathrm{and}\:\mathrm{RHS}\:\mathrm{always}\:\mathrm{odd} \\ $$$$\mathrm{Hence},\:\mathrm{log}_{\mathrm{2}} \:\mathrm{5}\:\mathrm{is}\:\mathrm{irrational} \\ $$

Answered by mrW2 last updated on 11/Mar/18

assume log_2 5 is rational, i.e. it can be expressed as log_2 5=(m/n) where m, n are integers and gcd(m,n)=1. ⇒2^(m/n) =5 ⇒2^m =5^n since 2 and 5 are co−prime, ⇒m=n=0. i.e. log_2 5 can not be expressed as (m/n), it′s irrational.

$${assume}\:\mathrm{log}_{\mathrm{2}} \:\mathrm{5}\:{is}\:{rational},\:{i}.{e}.\:{it}\:{can} \\ $$$${be}\:{expressed}\:{as}\: \\ $$$$\mathrm{log}_{\mathrm{2}} \:\mathrm{5}=\frac{{m}}{{n}} \\ $$$${where}\:{m},\:{n}\:{are}\:{integers}\:{and}\:{gcd}\left({m},{n}\right)=\mathrm{1}. \\ $$$$\Rightarrow\mathrm{2}^{\frac{{m}}{{n}}} =\mathrm{5} \\ $$$$\Rightarrow\mathrm{2}^{{m}} =\mathrm{5}^{{n}} \\ $$$${since}\:\mathrm{2}\:{and}\:\mathrm{5}\:{are}\:{co}−{prime}, \\ $$$$\Rightarrow{m}={n}=\mathrm{0}. \\ $$$${i}.{e}.\:\mathrm{log}_{\mathrm{2}} \:\mathrm{5}\:{can}\:{not}\:{be}\:{expressed}\:{as}\:\frac{{m}}{{n}}, \\ $$$${it}'{s}\:{irrational}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com