
Question Number 31595 by Nayon.Sm last updated on 11/Mar/18

Commented by Rasheed.Sindhi last updated on 11/Mar/18

$${a}=\mathrm{0},{b}=\mathrm{353} \\ $$
Commented by Joel578 last updated on 11/Mar/18
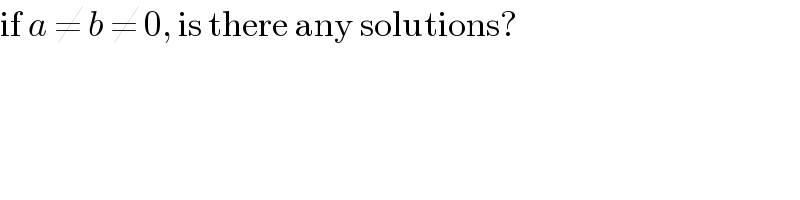
$$\mathrm{if}\:{a}\:\neq\:{b}\:\neq\:\mathrm{0},\:\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{solutions}? \\ $$
Answered by Rasheed.Sindhi last updated on 11/Mar/18

$$\mathrm{It}\:\mathrm{can}\:\mathrm{be}\:\mathrm{proved}\:\mathrm{that}\:\:\:\: \\ $$$$\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} ,\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} \:\&\:\mathrm{2mn}\:\mathrm{is}\:\mathrm{a}\:\mathrm{pathagorean} \\ $$$$\mathrm{triplet}\:\mathrm{for}\:\mathrm{m},\mathrm{n}\in\mathbb{N}\:\&\:\mathrm{m}>\mathrm{n}\:\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} =\mathrm{353} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{a}=\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{b}=\mathrm{2mn} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{n}^{\mathrm{2}} =\mathrm{353}−\mathrm{m}^{\mathrm{2}} \\ $$$$\mathrm{For}\:\mathrm{what}\:\mathrm{values}\:\mathrm{of}\:\mathrm{m}\:\:\mathrm{353}−\mathrm{m}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{perfect} \\ $$$$\mathrm{square}?\:\mathrm{Recall} \\ $$$$\mathrm{that}\:\mathrm{1}\leqslant\mathrm{m}^{\mathrm{2}} \leqslant\mathrm{353}\Rightarrow\mathrm{1}\:\leqslant\mathrm{m}\leqslant\sqrt{\mathrm{353}}=\mathrm{18} \\ $$$$\mathrm{So}\:\mathrm{testing}\:\mathrm{353}−\mathrm{1}^{\mathrm{2}} ,\mathrm{353}−\mathrm{2}^{\mathrm{2}} ,...,\mathrm{353}−\mathrm{18}^{\mathrm{2}} \\ $$$$\mathrm{we}\:'\mathrm{ll}\:\mathrm{find}\:\mathrm{that}\:\mathrm{m}=\mathrm{17},\mathrm{n}=\mathrm{8}\:. \\ $$$$\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} =\mathrm{17}^{\mathrm{2}} −\mathrm{8}^{\mathrm{2}} =\mathrm{225} \\ $$$$\mathrm{2mn}=\mathrm{2}×\mathrm{17}×\mathrm{8}=\mathrm{272} \\ $$$$\:\:\mathrm{272}^{\mathrm{2}} +\mathrm{225}^{\mathrm{2}} =\mathrm{353}^{\mathrm{2}} \\ $$
Answered by naka3546 last updated on 11/Mar/18

Commented by Rasheed.Sindhi last updated on 11/Mar/18
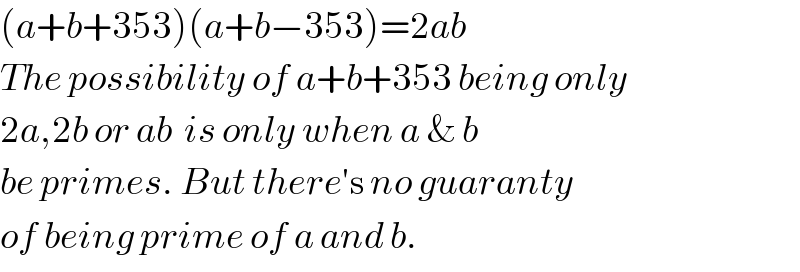
$$\left({a}+{b}+\mathrm{353}\right)\left({a}+{b}−\mathrm{353}\right)=\mathrm{2}{ab} \\ $$$${The}\:{possibility}\:{of}\:{a}+{b}+\mathrm{353}\:{being}\:{only} \\ $$$$\mathrm{2}{a},\mathrm{2}{b}\:{or}\:{ab}\:\:{is}\:{only}\:{when}\:{a}\:\&\:{b} \\ $$$${be}\:{primes}.\:{But}\:{there}'\mathrm{s}\:{no}\:{guaranty} \\ $$$${of}\:{being}\:{prime}\:{of}\:{a}\:{and}\:{b}. \\ $$
Commented by Rasheed.Sindhi last updated on 11/Mar/18
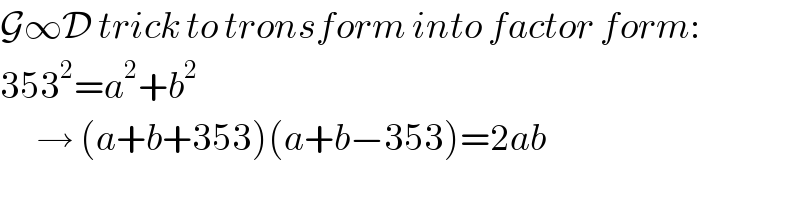
$$\mathcal{G}\infty\mathcal{D}\:{trick}\:{to}\:{tronsform}\:{into}\:{factor}\:{form}: \\ $$$$\mathrm{353}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\rightarrow\:\left({a}+{b}+\mathrm{353}\right)\left({a}+{b}−\mathrm{353}\right)=\mathrm{2}{ab} \\ $$
Commented by mrW2 last updated on 11/Mar/18
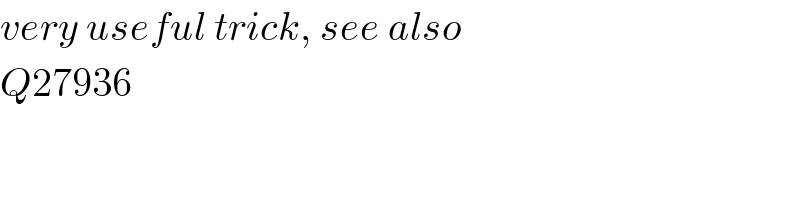
$${very}\:{useful}\:{trick},\:{see}\:{also} \\ $$$${Q}\mathrm{27936} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Mar/18
��
