
Question Number 31591 by Tinkutara last updated on 10/Mar/18
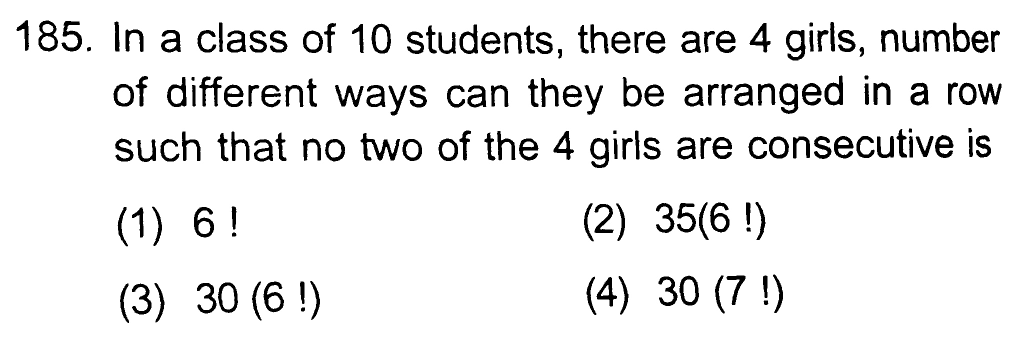
Commented by mrW2 last updated on 11/Mar/18
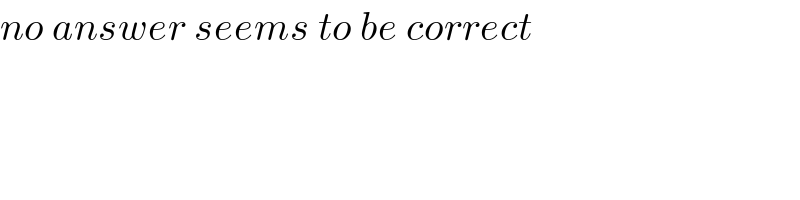
$${no}\:{answer}\:{seems}\:{to}\:{be}\:{correct} \\ $$
Commented by Tinkutara last updated on 11/Mar/18
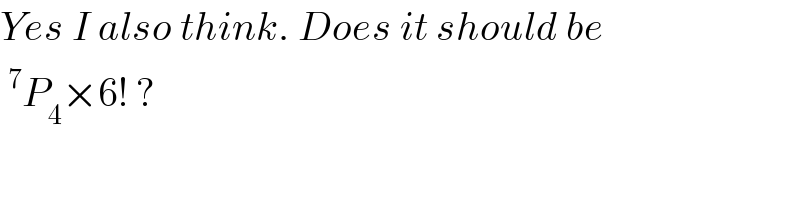
$${Yes}\:{I}\:{also}\:{think}.\:{Does}\:{it}\:{should}\:{be} \\ $$$$\:^{\mathrm{7}} {P}_{\mathrm{4}} ×\mathrm{6}!\:? \\ $$
Commented by mrW2 last updated on 11/Mar/18
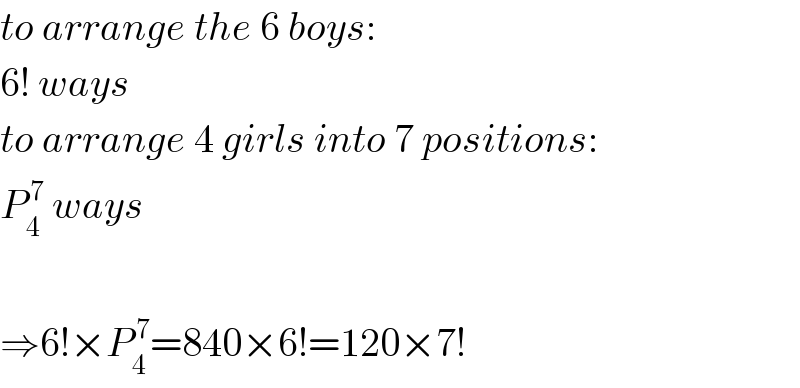
$${to}\:{arrange}\:{the}\:\mathrm{6}\:{boys}: \\ $$$$\mathrm{6}!\:{ways} \\ $$$${to}\:{arrange}\:\mathrm{4}\:{girls}\:{into}\:\mathrm{7}\:{positions}: \\ $$$${P}_{\mathrm{4}} ^{\:\mathrm{7}} \:{ways} \\ $$$$ \\ $$$$\Rightarrow\mathrm{6}!×{P}_{\mathrm{4}} ^{\:\mathrm{7}} =\mathrm{840}×\mathrm{6}!=\mathrm{120}×\mathrm{7}! \\ $$
Commented by Tinkutara last updated on 11/Mar/18
Thank you very much Sir! I got the answer. ������☺
Answered by MJS last updated on 11/Mar/18

$$\mathrm{the}\:\mathrm{girls}\:\mathrm{can}\:\mathrm{be}\:\mathrm{on}\:\mathrm{these}\:\mathrm{positions} \\ $$$$\left(\mathrm{0}\:\mathrm{stands}\:\mathrm{for}\:\mathrm{10}\right): \\ $$$$\mathrm{1357}\:\mathrm{1358}\:\mathrm{1359}\:\mathrm{1350} \\ $$$$\mathrm{1368}\:\mathrm{1369}\:\mathrm{1360} \\ $$$$\mathrm{1379}\:\mathrm{1370} \\ $$$$\mathrm{1380} \\ $$$$\mathrm{1468}\:\mathrm{1469}\:\mathrm{1460} \\ $$$$\mathrm{1479}\:\mathrm{1470} \\ $$$$\mathrm{1480} \\ $$$$\mathrm{1579}\:\mathrm{1570} \\ $$$$\mathrm{1580} \\ $$$$\mathrm{1680} \\ $$$$\mathrm{2468}\:\mathrm{2469}\:\mathrm{2460} \\ $$$$\mathrm{2479}\:\mathrm{2470} \\ $$$$\mathrm{2480} \\ $$$$\mathrm{2579}\:\mathrm{2570} \\ $$$$\mathrm{2580} \\ $$$$\mathrm{2680} \\ $$$$\mathrm{3579}\:\mathrm{3570} \\ $$$$\mathrm{3580} \\ $$$$\mathrm{3680} \\ $$$$\mathrm{4680} \\ $$$$\mathrm{so}\:\mathrm{it}'\mathrm{s}\:\mathrm{35}×\mathrm{4}!×\mathrm{6}!=\mathrm{5}×\mathrm{7}×\mathrm{4}!×\mathrm{6}!= \\ $$$$=\mathrm{5}!×\mathrm{7}! \\ $$
Commented by mrW2 last updated on 11/Mar/18

$${this}\:{is}\:{my}\:{solution}: \\ $$$${between}\:{two}\:{girls}\:{there}\:{must}\:{be}\:{at} \\ $$$${least}\:{one}\:{boy},\:{that}'{s}\:{to}\:{say}\:{the}\:{four} \\ $$$${girls}\:{can}\:{only}\:{be}\:{placed}\:{in}\:{the}\:{positions} \\ $$$${marked}\:{as}\:\circleddash: \\ $$$$\circleddash\circledast\circleddash\circledast\circleddash\circledast\circleddash\circledast\circleddash\circledast\circleddash\circledast\circleddash \\ $$$${where}\:\circledast\:{means}\:{a}\:{boy}. \\ $$$$ \\ $$$${following}\:{is}\:{e}.{g}.\:{a}\:{valid}\:{arrangement}: \\ $$$$\circleddash\circledast\square\circledast\circleddash\circledast\square\circledast\square\circledast\circleddash\circledast\square \\ $$$${where}\:\square\:{means}\:{a}\:{girl},\:\circleddash\:{means}\:{empty}. \\ $$$$ \\ $$$${to}\:{arrange}\:{the}\:\mathrm{6}\:{boys}\:\circledast:\:\mathrm{6}!\:{ways} \\ $$$${to}\:{arrange}\:{the}\:\mathrm{4}\:{girls}\:\square:\:{P}_{\mathrm{4}} ^{\:\mathrm{7}} \:{ways} \\ $$$$\Rightarrow{result}={P}_{\mathrm{4}} ^{\:\mathrm{7}} ×\mathrm{6}!\:{ways}. \\ $$$$ \\ $$$${generally}:\:{n}\:{students},\:{m}\:{girls} \\ $$$$\Rightarrow{P}_{{m}} ^{\:{n}−{m}+\mathrm{1}} ×\left({n}−{m}\right)! \\ $$
