
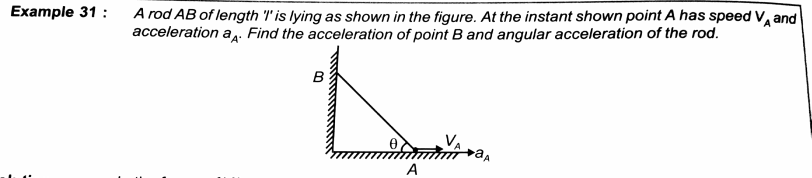
Question Number 31584 by Tinkutara last updated on 10/Mar/18
Answered by mrW2 last updated on 10/Mar/18
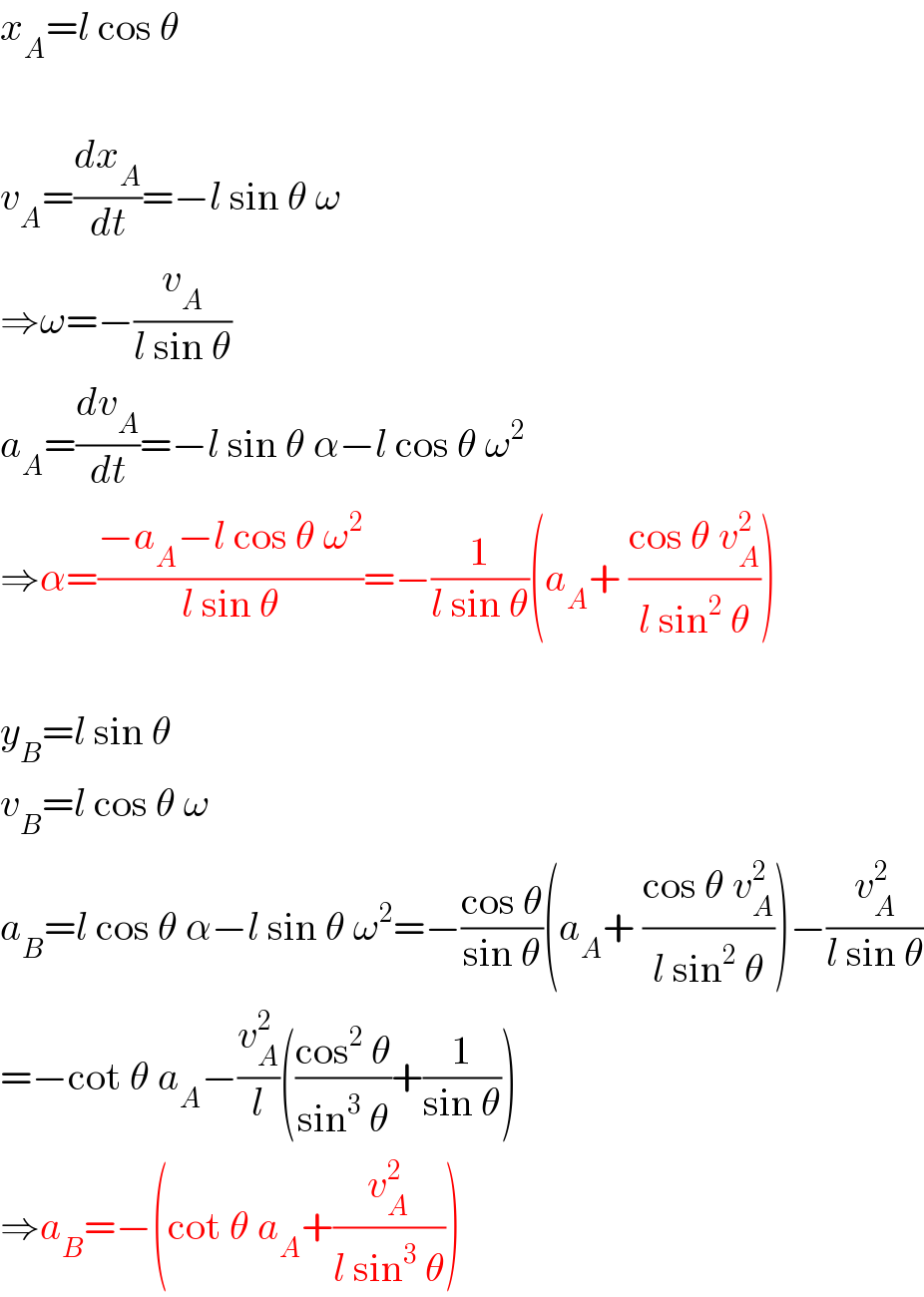
$${x}_{{A}} ={l}\:\mathrm{cos}\:\theta \\ $$$$ \\ $$$${v}_{{A}} =\frac{{dx}_{{A}} }{{dt}}=−{l}\:\mathrm{sin}\:\theta\:\omega \\ $$$$\Rightarrow\omega=−\frac{{v}_{{A}} }{{l}\:\mathrm{sin}\:\theta} \\ $$$${a}_{{A}} =\frac{{dv}_{{A}} }{{dt}}=−{l}\:\mathrm{sin}\:\theta\:\alpha−{l}\:\mathrm{cos}\:\theta\:\omega^{\mathrm{2}} \\ $$$$\Rightarrow\alpha=\frac{−{a}_{{A}} −{l}\:\mathrm{cos}\:\theta\:\omega^{\mathrm{2}} }{{l}\:\mathrm{sin}\:\theta}=−\frac{\mathrm{1}}{{l}\:\mathrm{sin}\:\theta}\left({a}_{{A}} +\:\frac{\mathrm{cos}\:\theta\:{v}_{{A}} ^{\mathrm{2}} }{{l}\:\mathrm{sin}^{\mathrm{2}} \:\theta}\right) \\ $$$$ \\ $$$${y}_{{B}} ={l}\:\mathrm{sin}\:\theta \\ $$$${v}_{{B}} ={l}\:\mathrm{cos}\:\theta\:\omega \\ $$$${a}_{{B}} ={l}\:\mathrm{cos}\:\theta\:\alpha−{l}\:\mathrm{sin}\:\theta\:\omega^{\mathrm{2}} =−\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\left({a}_{{A}} +\:\frac{\mathrm{cos}\:\theta\:{v}_{{A}} ^{\mathrm{2}} }{{l}\:\mathrm{sin}^{\mathrm{2}} \:\theta}\right)−\frac{{v}_{{A}} ^{\mathrm{2}} }{{l}\:\mathrm{sin}\:\theta} \\ $$$$=−\mathrm{cot}\:\theta\:{a}_{{A}} −\frac{{v}_{{A}} ^{\mathrm{2}} }{{l}}\left(\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{sin}^{\mathrm{3}} \:\theta}+\frac{\mathrm{1}}{\mathrm{sin}\:\theta}\right) \\ $$$$\Rightarrow{a}_{{B}} =−\left(\mathrm{cot}\:\theta\:{a}_{{A}} +\frac{{v}_{{A}} ^{\mathrm{2}} }{{l}\:\mathrm{sin}^{\mathrm{3}} \:\theta}\right) \\ $$
Commented by Tinkutara last updated on 10/Mar/18

Commented by Tinkutara last updated on 10/Mar/18

$${Do}\:{I}\:{need}\:{to}\:{further}\:{do}\:{vector}\:{sum} \\ $$$${of}\:{these}?\:{And}\:{how}\:{to}\:{find}\:\omega\:{and}\:{I}\alpha? \\ $$
Commented by Tinkutara last updated on 11/Mar/18
Please see it's my book solution but I can't understand that.
Commented by mrW2 last updated on 11/Mar/18

$${i}\:{can}\:{not}\:{help}\:{you}\:{sir}.\:{i}\:{personally} \\ $$$${won}'{t}\:{do}\:{in}\:{that}\:{way}\:{as}\:{the}\:{book}. \\ $$
Commented by Tinkutara last updated on 11/Mar/18
I am not asking you sir to solve that way. I am just asking that the book is correct to say that the final acceleration is the vector sum of that 3 so we need to find that? I highly appreciate your method!
