
Question Number 31573 by mondodotto@gmail.com last updated on 10/Mar/18
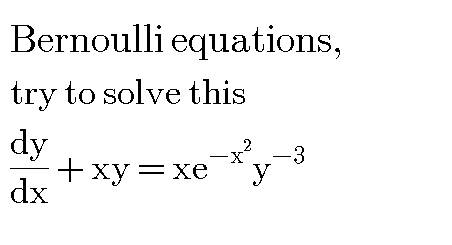
Commented by MJS last updated on 10/Mar/18
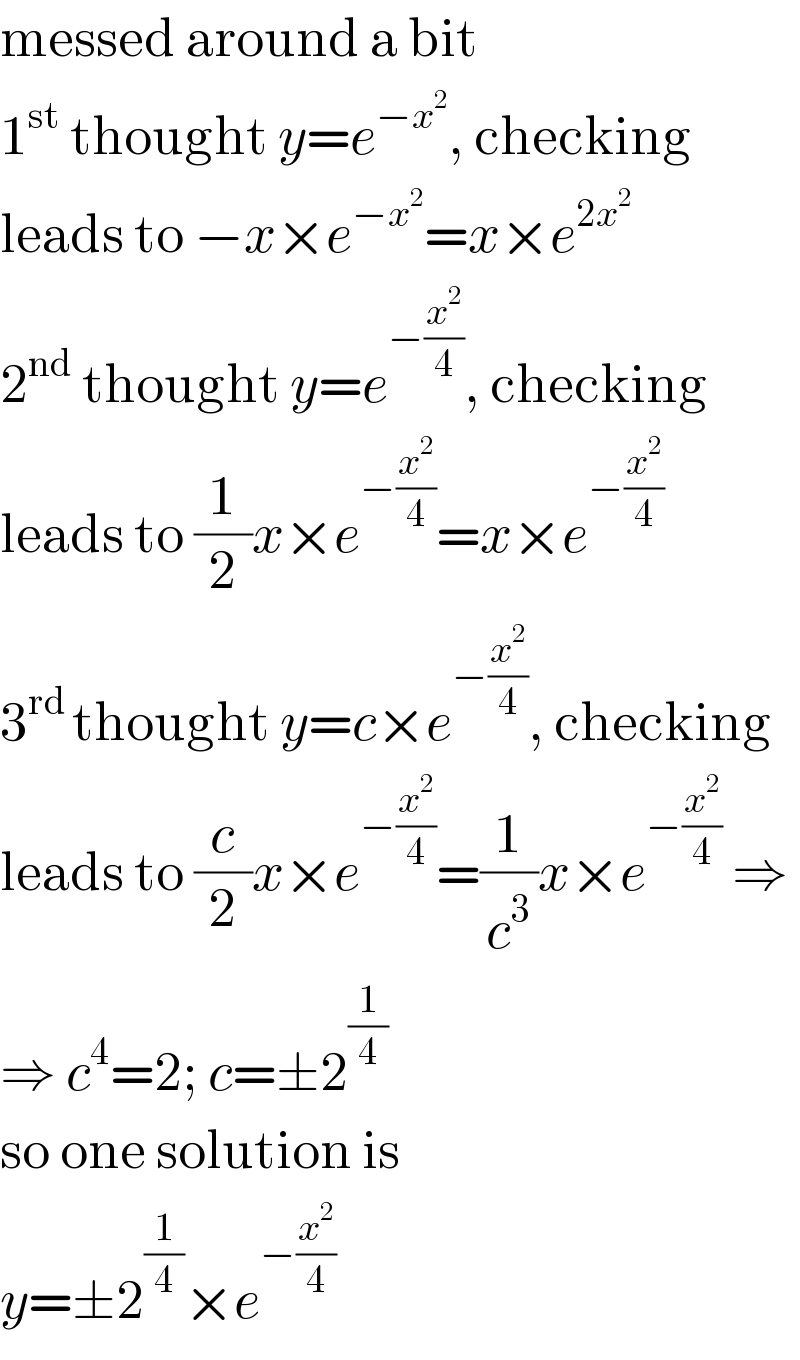
$$\mathrm{messed}\:\mathrm{around}\:\mathrm{a}\:\mathrm{bit} \\ $$$$\mathrm{1}^{\mathrm{st}} \:\mathrm{thought}\:{y}={e}^{−{x}^{\mathrm{2}} } ,\:\mathrm{checking} \\ $$$$\mathrm{leads}\:\mathrm{to}\:−{x}×{e}^{−{x}^{\mathrm{2}} } ={x}×{e}^{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{thought}\:{y}={e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} ,\:\mathrm{checking} \\ $$$$\mathrm{leads}\:\mathrm{to}\:\frac{\mathrm{1}}{\mathrm{2}}{x}×{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} ={x}×{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\mathrm{3}^{\mathrm{rd}\:} \mathrm{thought}\:{y}={c}×{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} ,\:\mathrm{checking} \\ $$$$\mathrm{leads}\:\mathrm{to}\:\frac{{c}}{\mathrm{2}}{x}×{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} =\frac{\mathrm{1}}{{c}^{\mathrm{3}} }{x}×{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \:\Rightarrow \\ $$$$\Rightarrow\:{c}^{\mathrm{4}} =\mathrm{2};\:{c}=\pm\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\mathrm{so}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{is} \\ $$$${y}=\pm\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} ×{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$
