
Question Number 31572 by mondodotto@gmail.com last updated on 10/Mar/18
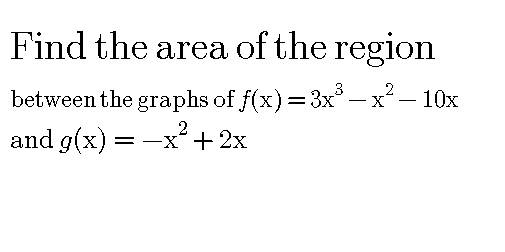
Answered by MJS last updated on 10/Mar/18
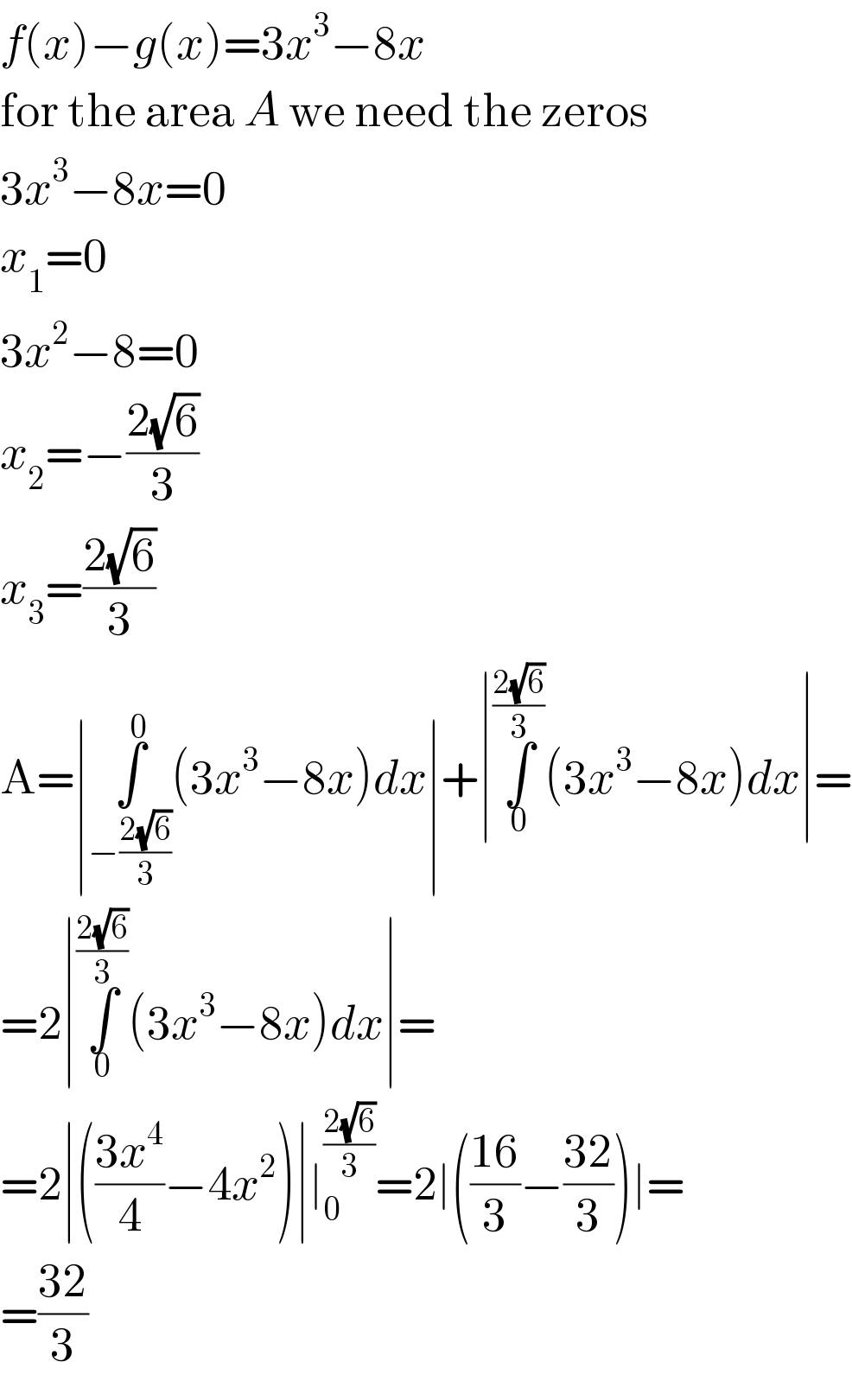
$${f}\left({x}\right)−{g}\left({x}\right)=\mathrm{3}{x}^{\mathrm{3}} −\mathrm{8}{x} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{area}\:{A}\:\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{zeros} \\ $$$$\mathrm{3}{x}^{\mathrm{3}} −\mathrm{8}{x}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{8}=\mathrm{0} \\ $$$${x}_{\mathrm{2}} =−\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\mathrm{A}=\mid\underset{−\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}} {\overset{\mathrm{0}} {\int}}\left(\mathrm{3}{x}^{\mathrm{3}} −\mathrm{8}{x}\right){dx}\mid+\mid\underset{\mathrm{0}} {\overset{\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}} {\int}}\left(\mathrm{3}{x}^{\mathrm{3}} −\mathrm{8}{x}\right){dx}\mid= \\ $$$$=\mathrm{2}\mid\underset{\mathrm{0}} {\overset{\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}} {\int}}\left(\mathrm{3}{x}^{\mathrm{3}} −\mathrm{8}{x}\right){dx}\mid= \\ $$$$=\mathrm{2}\mid\left(\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{4}}−\mathrm{4}{x}^{\mathrm{2}} \right)\mid\mid_{\mathrm{0}} ^{\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}} =\mathrm{2}\mid\left(\frac{\mathrm{16}}{\mathrm{3}}−\frac{\mathrm{32}}{\mathrm{3}}\right)\mid= \\ $$$$=\frac{\mathrm{32}}{\mathrm{3}} \\ $$
Commented by mondodotto@gmail.com last updated on 10/Mar/18

$$\mathrm{thanx}\: \\ $$
