
Question Number 27055 by Joel578 last updated on 01/Jan/18
Commented by Joel578 last updated on 01/Jan/18

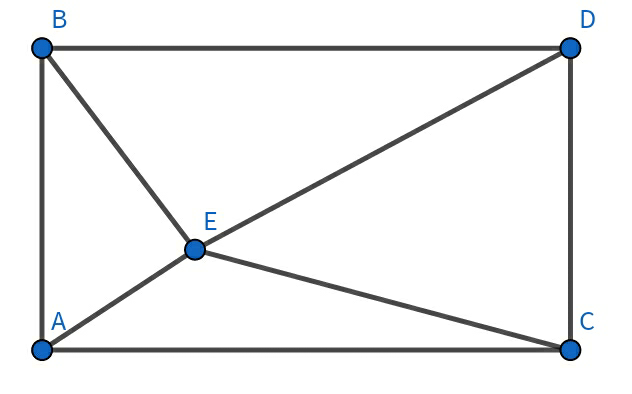
$${EB}\:=\:\mathrm{4} \\ $$$${ED}\:=\:\mathrm{8} \\ $$$${EC}\:=\:\mathrm{7} \\ $$$$\mathrm{Find}\:{EA} \\ $$
Answered by mrW1 last updated on 01/Jan/18
Commented by mrW1 last updated on 01/Jan/18
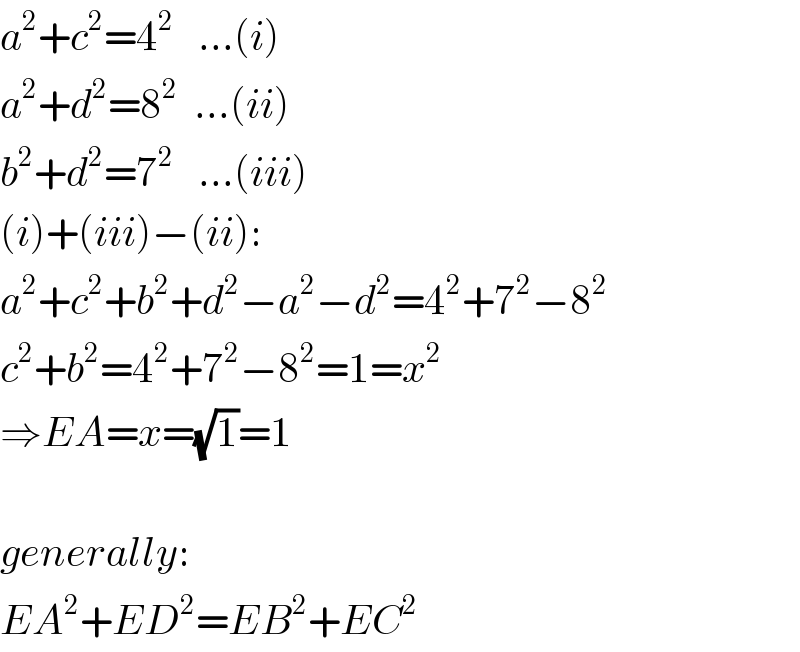
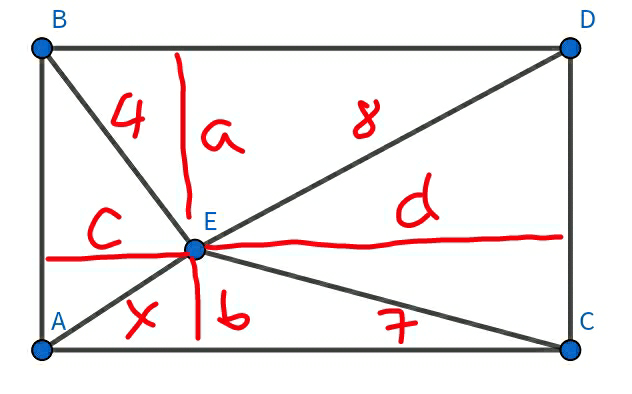
$${a}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$${a}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{8}^{\mathrm{2}} \:\:...\left({ii}\right) \\ $$$${b}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} \:\:\:...\left({iii}\right) \\ $$$$\left({i}\right)+\left({iii}\right)−\left({ii}\right): \\ $$$${a}^{\mathrm{2}} +{c}^{\mathrm{2}} +{b}^{\mathrm{2}} +{d}^{\mathrm{2}} −{a}^{\mathrm{2}} −{d}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{8}^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{8}^{\mathrm{2}} =\mathrm{1}={x}^{\mathrm{2}} \\ $$$$\Rightarrow{EA}={x}=\sqrt{\mathrm{1}}=\mathrm{1} \\ $$$$ \\ $$$${generally}: \\ $$$${EA}^{\mathrm{2}} +{ED}^{\mathrm{2}} ={EB}^{\mathrm{2}} +{EC}^{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Jan/18

$$\mathcal{E}{xcellent}! \\ $$
Commented by Joel578 last updated on 02/Jan/18
$${thank}\:{you}\:{very}\:{much} \\ $$
