
Question Number 25457 by Tinkutara last updated on 10/Dec/17
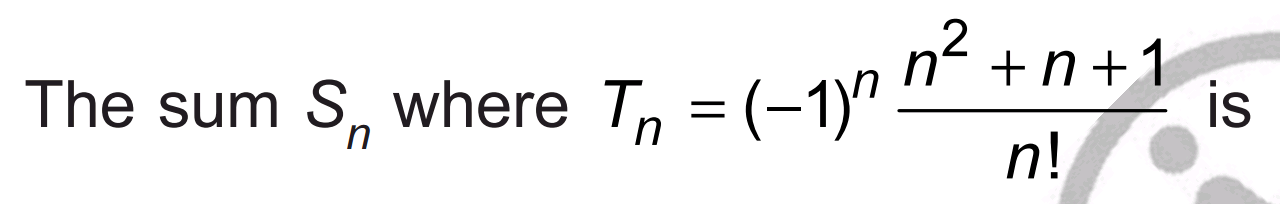
Answered by prakash jain last updated on 10/Dec/17
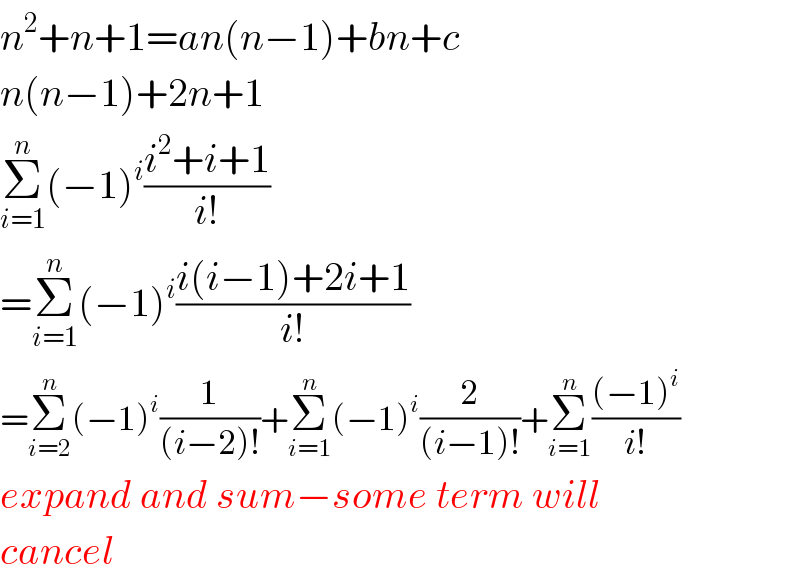
$${n}^{\mathrm{2}} +{n}+\mathrm{1}={an}\left({n}−\mathrm{1}\right)+{bn}+{c} \\ $$$${n}\left({n}−\mathrm{1}\right)+\mathrm{2}{n}+\mathrm{1} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \frac{{i}^{\mathrm{2}} +{i}+\mathrm{1}}{{i}!} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \frac{{i}\left({i}−\mathrm{1}\right)+\mathrm{2}{i}+\mathrm{1}}{{i}!} \\ $$$$=\underset{{i}=\mathrm{2}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \frac{\mathrm{1}}{\left({i}−\mathrm{2}\right)!}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \frac{\mathrm{2}}{\left({i}−\mathrm{1}\right)!}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{i}} }{{i}!} \\ $$$${expand}\:{and}\:{sum}−{some}\:{term}\:{will} \\ $$$${cancel} \\ $$
Commented by Tinkutara last updated on 10/Dec/17
Yes Sir thanks it telescopes
