
Question Number 24817 by A1B1C1D1 last updated on 26/Nov/17
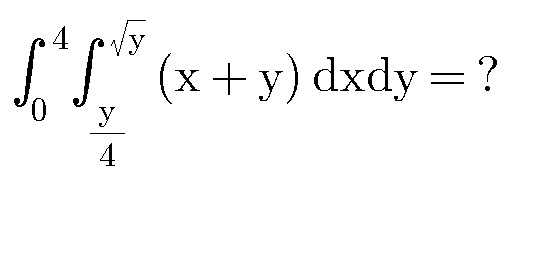
Answered by mrW1 last updated on 26/Nov/17
![=∫_0 ^( 4) [(1/2)(y−(y^2 /(16)))+y((√y)−(y/4))]dy =∫_0 ^( 4) ((y/2)−((9y^2 )/(32))+y^(3/2) )dy =[(y^2 /4)−((3y^3 )/(32))+((2y^(5/2) )/5)]_0 ^4 =((16)/4)−((3×64)/(32))+((2×32)/5) =((54)/5)](Q24818.png)
$$=\int_{\mathrm{0}} ^{\:\mathrm{4}} \left[\frac{\mathrm{1}}{\mathrm{2}}\left({y}−\frac{{y}^{\mathrm{2}} }{\mathrm{16}}\right)+{y}\left(\sqrt{{y}}−\frac{{y}}{\mathrm{4}}\right)\right]{dy} \\ $$$$=\int_{\mathrm{0}} ^{\:\mathrm{4}} \left(\frac{{y}}{\mathrm{2}}−\frac{\mathrm{9}{y}^{\mathrm{2}} }{\mathrm{32}}+{y}^{\frac{\mathrm{3}}{\mathrm{2}}} \right){dy} \\ $$$$=\left[\frac{{y}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{3}{y}^{\mathrm{3}} }{\mathrm{32}}+\frac{\mathrm{2}{y}^{\frac{\mathrm{5}}{\mathrm{2}}} }{\mathrm{5}}\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$=\frac{\mathrm{16}}{\mathrm{4}}−\frac{\mathrm{3}×\mathrm{64}}{\mathrm{32}}+\frac{\mathrm{2}×\mathrm{32}}{\mathrm{5}} \\ $$$$=\frac{\mathrm{54}}{\mathrm{5}} \\ $$
Commented by A1B1C1D1 last updated on 27/Nov/17

$$\mathrm{Thank}\:\mathrm{you}. \\ $$
