Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 24576 by math solver last updated on 21/Nov/17

Commented by math solver last updated on 21/Nov/17

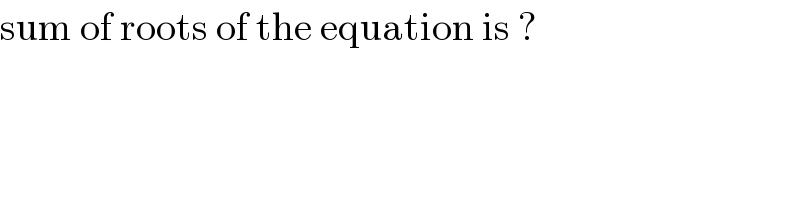
sum of roots of the equation is ?

$$\mathrm{sum}\:\mathrm{of}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{is}\:? \\ $$

Answered by mrW1 last updated on 21/Nov/17

((x+1)/2)=log_2 (2^x +3)−((log_2 (1980−2^(−x) ) )/(log_2 4)) ((x+1)/2)=log_2 (2^x +3)−((log_2 (1980−2^(−x) ) )/2) x+1=2log_2 (2^x +3)−log_2 (1980−2^(−x) ) x+1=log_2 (((2^x +3)^2 )/(1980−2^(−x) )) 2^(x+1) =(((2^x +3)^2 )/(1980−2^(−x) )) 2×2^x =(((2^x +3)^2 )/(1980−2^(−x) )) 2×1980×2^x −2=(2^x +3)^2 =(2^x )^2 +6(2^x )+9 (2^x )^2 −3954(2^x )+11=0 ...(i) ⇒2^x =((3954±(√(3954^2 −4×11)))/2) ⇒2^x =1977±(√(3908518)) ⇒x=log_2 (1977±(√(3908518))) (≈−8.49 or 11.95) ⇒Σx=log_2 (1977+(√(3908518)))(1977−(√(3908518))) ⇒Σx=log_2 (1977^2 −3908518)=log_2 11≈3.46 or directly from (i) 2^x_1 ×2^x_2 =11 ⇒2^(x_1 +x_2 ) =11 ⇒x_1 +x_2 =log_2 11

$$\frac{{x}+\mathrm{1}}{\mathrm{2}}=\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{2}^{{x}} +\mathrm{3}\right)−\frac{\mathrm{log}_{\mathrm{2}} \left(\mathrm{1980}−\mathrm{2}^{−{x}} \right)\:}{\mathrm{log}_{\mathrm{2}} \:\mathrm{4}} \\ $$$$\frac{{x}+\mathrm{1}}{\mathrm{2}}=\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{2}^{{x}} +\mathrm{3}\right)−\frac{\mathrm{log}_{\mathrm{2}} \left(\mathrm{1980}−\mathrm{2}^{−{x}} \right)\:}{\mathrm{2}} \\ $$$${x}+\mathrm{1}=\mathrm{2log}_{\mathrm{2}} \:\left(\mathrm{2}^{{x}} +\mathrm{3}\right)−\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{1980}−\mathrm{2}^{−{x}} \right) \\ $$$${x}+\mathrm{1}=\mathrm{log}_{\mathrm{2}} \:\frac{\left(\mathrm{2}^{{x}} +\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{1980}−\mathrm{2}^{−{x}} } \\ $$$$\mathrm{2}^{{x}+\mathrm{1}} =\frac{\left(\mathrm{2}^{{x}} +\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{1980}−\mathrm{2}^{−{x}} } \\ $$$$\mathrm{2}×\mathrm{2}^{{x}} =\frac{\left(\mathrm{2}^{{x}} +\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{1980}−\mathrm{2}^{−{x}} } \\ $$$$\mathrm{2}×\mathrm{1980}×\mathrm{2}^{{x}} −\mathrm{2}=\left(\mathrm{2}^{{x}} +\mathrm{3}\right)^{\mathrm{2}} =\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} +\mathrm{6}\left(\mathrm{2}^{{x}} \right)+\mathrm{9} \\ $$$$\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} −\mathrm{3954}\left(\mathrm{2}^{{x}} \right)+\mathrm{11}=\mathrm{0}\:\:\:\:\:\:...\left({i}\right) \\ $$$$\Rightarrow\mathrm{2}^{{x}} =\frac{\mathrm{3954}\pm\sqrt{\mathrm{3954}^{\mathrm{2}} −\mathrm{4}×\mathrm{11}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}^{{x}} =\mathrm{1977}\pm\sqrt{\mathrm{3908518}} \\ $$$$\Rightarrow{x}=\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{1977}\pm\sqrt{\mathrm{3908518}}\right) \\ $$$$\left(\approx−\mathrm{8}.\mathrm{49}\:{or}\:\mathrm{11}.\mathrm{95}\right) \\ $$$$\Rightarrow\Sigma{x}=\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{1977}+\sqrt{\mathrm{3908518}}\right)\left(\mathrm{1977}−\sqrt{\mathrm{3908518}}\right) \\ $$$$\Rightarrow\Sigma{x}=\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{1977}^{\mathrm{2}} −\mathrm{3908518}\right)=\mathrm{log}_{\mathrm{2}} \:\mathrm{11}\approx\mathrm{3}.\mathrm{46} \\ $$$$ \\ $$$${or}\:{directly}\:{from}\:\left({i}\right) \\ $$$$\mathrm{2}^{{x}_{\mathrm{1}} } ×\mathrm{2}^{{x}_{\mathrm{2}} } =\mathrm{11} \\ $$$$\Rightarrow\mathrm{2}^{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} } =\mathrm{11} \\ $$$$\Rightarrow{x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\mathrm{log}_{\mathrm{2}} \:\mathrm{11} \\ $$

Commented by mrW1 last updated on 22/Nov/17

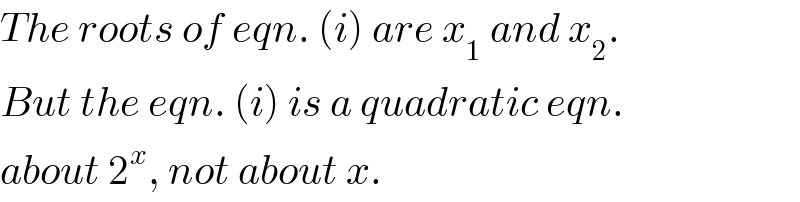
The roots of eqn. (i) are x_1 and x_2 . But the eqn. (i) is a quadratic eqn. about 2^x , not about x.

$${The}\:{roots}\:{of}\:{eqn}.\:\left({i}\right)\:{are}\:{x}_{\mathrm{1}} \:{and}\:{x}_{\mathrm{2}} . \\ $$$${But}\:{the}\:{eqn}.\:\left({i}\right)\:{is}\:{a}\:{quadratic}\:{eqn}.\: \\ $$$${about}\:\mathrm{2}^{{x}} ,\:{not}\:{about}\:{x}. \\ $$

Commented by math solver last updated on 22/Nov/17

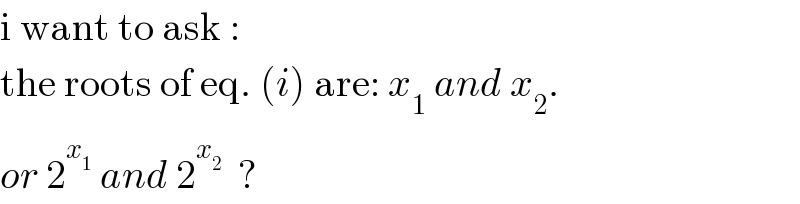
i want to ask : the roots of eq. (i) are: x_1 and x_2 . or 2^x_1 and 2^x_2 ?

$$\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{ask}\:: \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{eq}.\:\left({i}\right)\:\mathrm{are}:\:{x}_{\mathrm{1}} \:{and}\:{x}_{\mathrm{2}} . \\ $$$${or}\:\mathrm{2}^{{x}_{\mathrm{1}} } \:{and}\:\mathrm{2}^{{x}_{\mathrm{2}} } \:\:? \\ $$

Commented by mrW1 last updated on 22/Nov/17

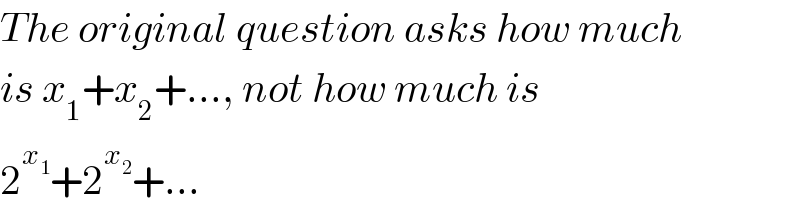
The original question asks how much is x_1 +x_2 +..., not how much is 2^x_1 +2^x_2 +...

$${The}\:{original}\:{question}\:{asks}\:{how}\:{much} \\ $$$${is}\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +...,\:{not}\:{how}\:{much}\:{is} \\ $$$$\mathrm{2}^{{x}_{\mathrm{1}} } +\mathrm{2}^{{x}_{\mathrm{2}} } +... \\ $$

Commented by math solver last updated on 22/Nov/17

thank you sir!

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com