
Question Number 23960 by ajfour last updated on 10/Nov/17
Commented by ajfour last updated on 10/Nov/17

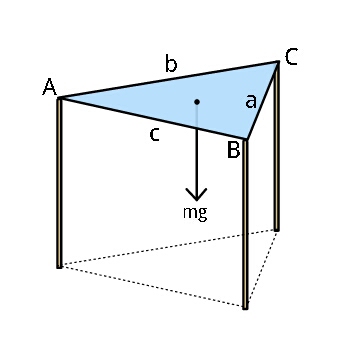
$${Find}\:{the}\:{Normal}\:{reaction}\:{forces} \\ $$$${at}\:{the}\:{foot}\:{of}\:{the}\:{three}\:{legs}\: \\ $$$${supporting}\:{a}\:{uniform}\:{horizontal} \\ $$$${triangular}\:{table}\:{top}\:{of}\:{mass}\:{m}, \\ $$$${in}\:{terms}\:{of}\:{the}\:{weight}\:\boldsymbol{{mg}}. \\ $$$$ \\ $$
Commented by mrW1 last updated on 10/Nov/17
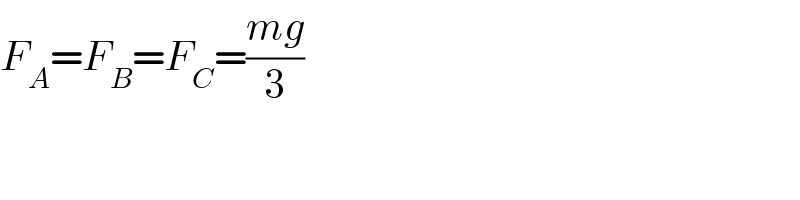
$${F}_{{A}} ={F}_{{B}} ={F}_{{C}} =\frac{{mg}}{\mathrm{3}} \\ $$
Commented by Physics lover last updated on 10/Nov/17
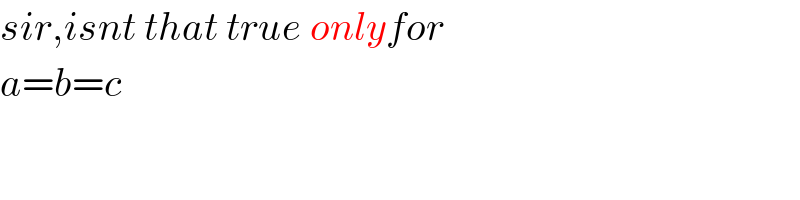
$${sir},{isnt}\:{that}\:{true}\:{onlyfor} \\ $$$${a}={b}={c} \\ $$
Commented by Physics lover last updated on 10/Nov/17

$$??? \\ $$
Answered by ajfour last updated on 10/Nov/17
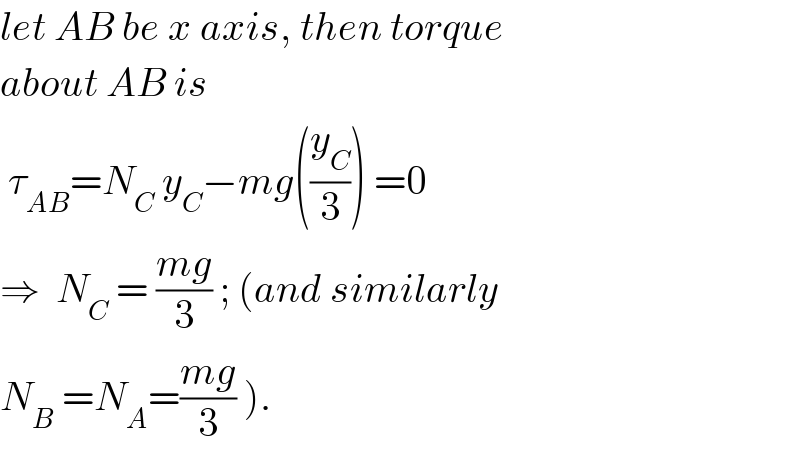
$${let}\:{AB}\:{be}\:{x}\:{axis},\:{then}\:{torque}\: \\ $$$${about}\:{AB}\:{is} \\ $$$$\:\tau_{{AB}} ={N}_{{C}} \:{y}_{{C}} −{mg}\left(\frac{{y}_{{C}} }{\mathrm{3}}\right)\:=\mathrm{0} \\ $$$$\Rightarrow\:\:{N}_{{C}} \:=\:\frac{{mg}}{\mathrm{3}}\:;\:\left({and}\:{similarly}\right. \\ $$$$\left.{N}_{{B}} \:={N}_{{A}} =\frac{{mg}}{\mathrm{3}}\:\right). \\ $$
Commented by mrW1 last updated on 10/Nov/17
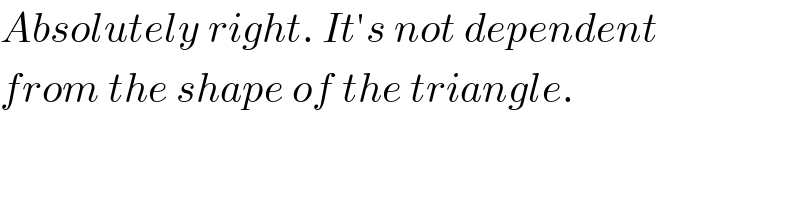
$${Absolutely}\:{right}.\:{It}'{s}\:{not}\:{dependent} \\ $$$${from}\:{the}\:{shape}\:{of}\:{the}\:{triangle}. \\ $$
