
Question Number 23688 by A1B1C1D1 last updated on 04/Nov/17
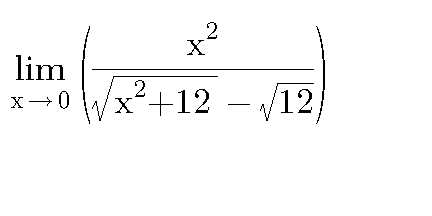
Answered by $@ty@m last updated on 04/Nov/17

$${Use}\:{method}\:{of}\:{rationalization} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{{x}^{\mathrm{2}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{12}}+\sqrt{\mathrm{12}}\right)}{{x}^{\mathrm{2}} +\mathrm{12}−\mathrm{12}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{{x}^{\mathrm{2}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{12}}+\sqrt{\mathrm{12}}\right)}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{12}}+\sqrt{\mathrm{12}}\right) \\ $$$$=\sqrt{\mathrm{12}}+\sqrt{\mathrm{12}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{12}} \\ $$$$=\mathrm{4}\sqrt{\mathrm{3}} \\ $$
