
Question Number 22730 by selestian last updated on 22/Oct/17
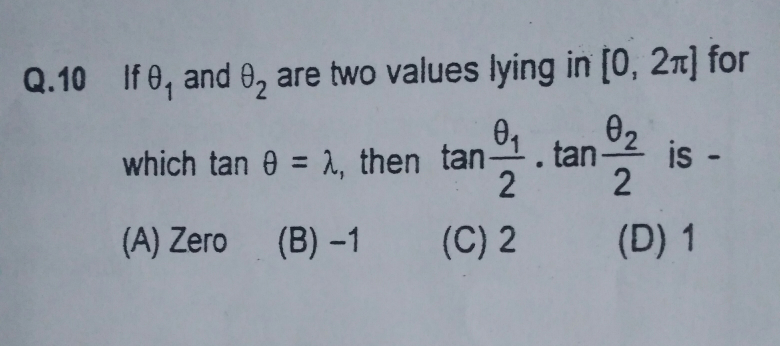
Commented by math solver last updated on 22/Oct/17

$$−\mathrm{1}.\:{we}\:{know}\:{tan}\:{is}\:{positive}\:{in}\: \\ $$$$\mathrm{1}{st}\:{and}\:\mathrm{3}{rd}\:{quadrant}\:. \\ $$$${so}\:{there}\:{are}\:{infinite}\:{values}\:{which} \\ $$$${we}\:{can}\:{take}\:. \\ $$$${say}\:{we}\:{take}\:\mathrm{60}\:{degree}\:{and}\:\mathrm{240}\:{degree}. \\ $$
Commented by selestian last updated on 22/Oct/17
$${yes}\:{you}\:{are}\:{right}\:{thAnks}\:{i}\:{got}\:{the}\:{answer} \\ $$$$ \\ $$
Answered by ajfour last updated on 22/Oct/17
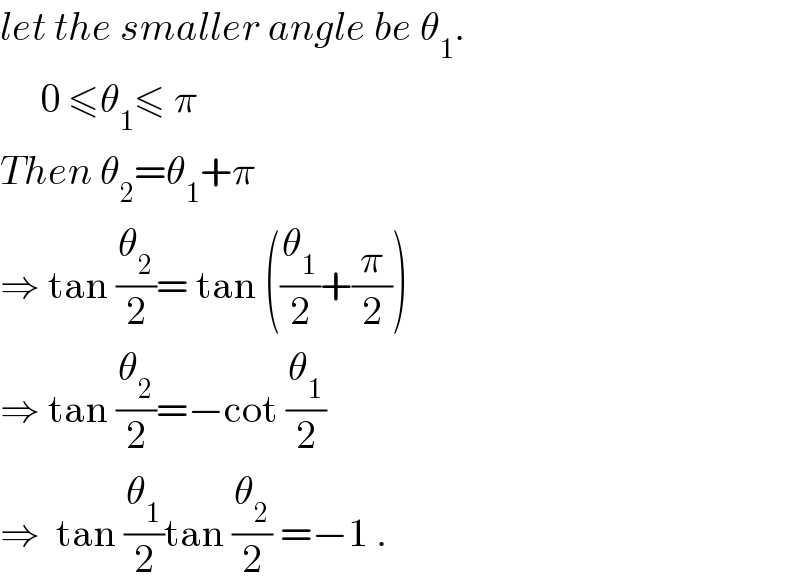
$${let}\:{the}\:{smaller}\:{angle}\:{be}\:\theta_{\mathrm{1}} . \\ $$$$\:\:\:\:\:\mathrm{0}\:\leqslant\theta_{\mathrm{1}} \leqslant\:\pi \\ $$$${Then}\:\theta_{\mathrm{2}} =\theta_{\mathrm{1}} +\pi \\ $$$$\Rightarrow\:\mathrm{tan}\:\frac{\theta_{\mathrm{2}} }{\mathrm{2}}=\:\mathrm{tan}\:\left(\frac{\theta_{\mathrm{1}} }{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\mathrm{tan}\:\frac{\theta_{\mathrm{2}} }{\mathrm{2}}=−\mathrm{cot}\:\frac{\theta_{\mathrm{1}} }{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\frac{\theta_{\mathrm{1}} }{\mathrm{2}}\mathrm{tan}\:\frac{\theta_{\mathrm{2}} }{\mathrm{2}}\:=−\mathrm{1}\:. \\ $$
