Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 219423 by SdC355 last updated on 24/Apr/25

Answered by SdC355 last updated on 24/Apr/25

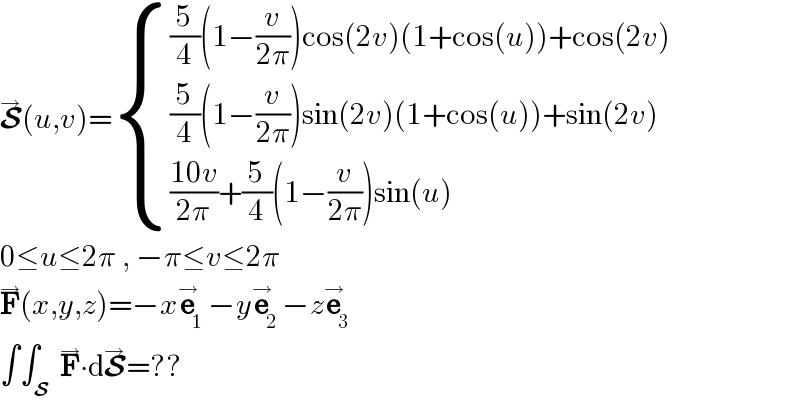
S^→ (u,v)= { (((5/4)(1−(v/(2π)))cos(2v)(1+cos(u))+cos(2v))),(((5/4)(1−(v/(2π)))sin(2v)(1+cos(u))+sin(2v))),((((10v)/(2π))+(5/4)(1−(v/(2π)))sin(u))) :} 0≤u≤2π , −π≤v≤2π F^→ (x,y,z)=−xe_1 ^→ −ye_2 ^→ −ze_3 ^→ ∫∫_S F^→ ∙dS^→ =??

$$\overset{\rightarrow} {\boldsymbol{\mathcal{S}}}\left({u},{v}\right)=\begin{cases}{\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{1}−\frac{{v}}{\mathrm{2}\pi}\right)\mathrm{cos}\left(\mathrm{2}{v}\right)\left(\mathrm{1}+\mathrm{cos}\left({u}\right)\right)+\mathrm{cos}\left(\mathrm{2}{v}\right)}\\{\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{1}−\frac{{v}}{\mathrm{2}\pi}\right)\mathrm{sin}\left(\mathrm{2}{v}\right)\left(\mathrm{1}+\mathrm{cos}\left({u}\right)\right)+\mathrm{sin}\left(\mathrm{2}{v}\right)}\\{\frac{\mathrm{10}{v}}{\mathrm{2}\pi}+\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{1}−\frac{{v}}{\mathrm{2}\pi}\right)\mathrm{sin}\left({u}\right)}\end{cases} \\ $$$$\mathrm{0}\leq{u}\leq\mathrm{2}\pi\:,\:−\pi\leq{v}\leq\mathrm{2}\pi \\ $$$$\overset{\rightarrow} {\boldsymbol{\mathrm{F}}}\left({x},{y},{z}\right)=−{x}\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{1}} −{y}\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{2}} −{z}\overset{\rightarrow} {\boldsymbol{\mathrm{e}}}_{\mathrm{3}} \\ $$$$\int\int_{\boldsymbol{\mathcal{S}}} \:\overset{\rightarrow} {\boldsymbol{\mathrm{F}}}\centerdot\mathrm{d}\overset{\rightarrow} {\boldsymbol{\mathcal{S}}}=?? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com