
Question Number 219384 by mnjuly1970 last updated on 23/Apr/25
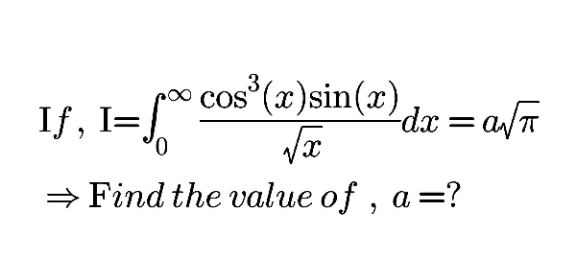
Answered by SdC355 last updated on 24/Apr/25
![∫ (dx/( (√x))) cos^3 (x)sin(x)=I ∫ (dx/( x)) (√x)cos^3 (x)sin(x)=∫ (dx/x) (√x)cos^2 (x)cos(x)sin(x) ∫ (dx/( 2x)) (√x)cos^2 (x)sin(2x)=∫ dx (e^(−xt) /x)(√x)cos^2 (x)sin(2x) ∫_( t) ^( ∞) dw L_w {(√x)cos^2 (x)sin(2x)}= ((√π)/(32)) i∫_( t) ^( ∞) dw {(2/( (√((w+2i)^3 ))))−(1/( (√((w−4i)^3 ))))+(1/( (√((w+4i)^3 ))))−(2/( (√((w−2i)^3 ))))} =[−((√π)/(32)) i{(4/( (√(w+2i))))−(2/( (√(w−4i))))+(2/( (√(w+4i))))−(4/( (√(w−2i))))}]_(w=t) ^(w=∞) ((√π)/(32)) i{(4/( (√(t+2i))))−(2/( (√(t−4i))))+(2/( (√(t+4i))))−(4/( (√(t−2i))))} t=0 ((√π)/(32)) i{(4/( (√(2i))))−(2/( (√(−4i))))+(2/( (√(4i))))−(4/( (√(−2i))))}=((4+(√2))/(32))(√π) ∴ α=((4+(√2))/(32))](Q219385.png)
$$\int\:\:\:\frac{\mathrm{d}{x}}{\:\sqrt{{x}}}\:\mathrm{cos}^{\mathrm{3}} \left({x}\right)\mathrm{sin}\left({x}\right)={I} \\ $$$$\int\:\:\:\frac{\mathrm{d}{x}}{\:{x}}\:\sqrt{{x}}\mathrm{cos}^{\mathrm{3}} \left({x}\right)\mathrm{sin}\left({x}\right)=\int\:\:\:\frac{\mathrm{d}{x}}{{x}}\:\sqrt{{x}}\mathrm{cos}^{\mathrm{2}} \left({x}\right)\mathrm{cos}\left({x}\right)\mathrm{sin}\left({x}\right) \\ $$$$\int\:\:\frac{\mathrm{d}{x}}{\:\mathrm{2}{x}}\:\sqrt{{x}}\mathrm{cos}^{\mathrm{2}} \left({x}\right)\mathrm{sin}\left(\mathrm{2}{x}\right)=\int\:\:\mathrm{d}{x}\:\frac{{e}^{−{xt}} }{{x}}\sqrt{{x}}\mathrm{cos}^{\mathrm{2}} \left({x}\right)\mathrm{sin}\left(\mathrm{2}{x}\right) \\ $$$$\int_{\:{t}} ^{\:\infty} \:\mathrm{d}{w}\:\mathcal{L}_{{w}} \left\{\sqrt{{x}}\mathrm{cos}^{\mathrm{2}} \left({x}\right)\mathrm{sin}\left(\mathrm{2}{x}\right)\right\}= \\ $$$$\frac{\sqrt{\pi}}{\mathrm{32}}\:\boldsymbol{{i}}\int_{\:{t}} ^{\:\infty} \:\mathrm{d}{w}\:\left\{\frac{\mathrm{2}}{\:\sqrt{\left({w}+\mathrm{2}\boldsymbol{{i}}\right)^{\mathrm{3}} }}−\frac{\mathrm{1}}{\:\sqrt{\left({w}−\mathrm{4}\boldsymbol{{i}}\right)^{\mathrm{3}} }}+\frac{\mathrm{1}}{\:\sqrt{\left({w}+\mathrm{4}\boldsymbol{{i}}\right)^{\mathrm{3}} }}−\frac{\mathrm{2}}{\:\sqrt{\left({w}−\mathrm{2}\boldsymbol{{i}}\right)^{\mathrm{3}} }}\right\} \\ $$$$=\left[−\frac{\sqrt{\pi}}{\mathrm{32}}\:\boldsymbol{{i}}\left\{\frac{\mathrm{4}}{\:\sqrt{{w}+\mathrm{2}\boldsymbol{{i}}}}−\frac{\mathrm{2}}{\:\sqrt{{w}−\mathrm{4}\boldsymbol{{i}}}}+\frac{\mathrm{2}}{\:\sqrt{{w}+\mathrm{4}\boldsymbol{{i}}}}−\frac{\mathrm{4}}{\:\sqrt{{w}−\mathrm{2}\boldsymbol{{i}}}}\right\}\right]_{{w}={t}} ^{{w}=\infty} \\ $$$$\frac{\sqrt{\pi}}{\mathrm{32}}\:\boldsymbol{{i}}\left\{\frac{\mathrm{4}}{\:\sqrt{{t}+\mathrm{2}\boldsymbol{{i}}}}−\frac{\mathrm{2}}{\:\sqrt{{t}−\mathrm{4}\boldsymbol{{i}}}}+\frac{\mathrm{2}}{\:\sqrt{{t}+\mathrm{4}\boldsymbol{{i}}}}−\frac{\mathrm{4}}{\:\sqrt{{t}−\mathrm{2}\boldsymbol{{i}}}}\right\} \\ $$$${t}=\mathrm{0} \\ $$$$\frac{\sqrt{\pi}}{\mathrm{32}}\:\boldsymbol{{i}}\left\{\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}\boldsymbol{{i}}}}−\frac{\mathrm{2}}{\:\sqrt{−\mathrm{4}\boldsymbol{{i}}}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}\boldsymbol{{i}}}}−\frac{\mathrm{4}}{\:\sqrt{−\mathrm{2}\boldsymbol{{i}}}}\right\}=\frac{\mathrm{4}+\sqrt{\mathrm{2}}}{\mathrm{32}}\sqrt{\pi} \\ $$$$\therefore\:\alpha=\frac{\mathrm{4}+\sqrt{\mathrm{2}}}{\mathrm{32}} \\ $$
Commented by mnjuly1970 last updated on 23/Apr/25
$${thanks}\:{alot}\:{bravo}\:{sir} \\ $$
