Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 219243 by mnjuly1970 last updated on 21/Apr/25

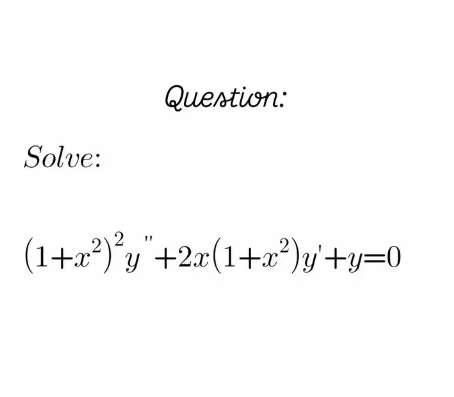
Commented by mr W last updated on 23/Apr/25

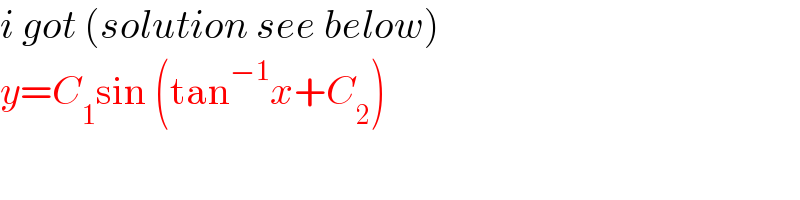
i got (solution see below) y=C_1 sin (tan^(−1) x+C_2 )

$${i}\:{got}\:\left({solution}\:{see}\:{below}\right) \\ $$$${y}={C}_{\mathrm{1}} \mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right) \\ $$

Commented by mr W last updated on 22/Apr/25

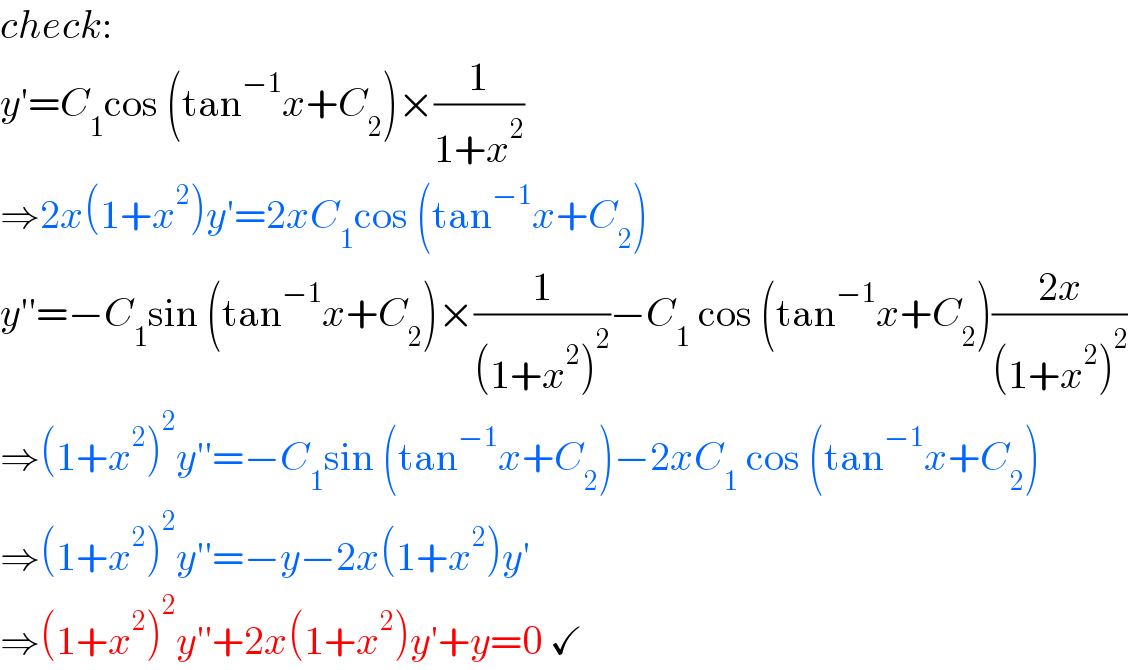
check: y′=C_1 cos (tan^(−1) x+C_2 )×(1/(1+x^2 )) ⇒2x(1+x^2 )y′=2xC_1 cos (tan^(−1) x+C_2 ) y′′=−C_1 sin (tan^(−1) x+C_2 )×(1/((1+x^2 )^2 ))−C_1 cos (tan^(−1) x+C_2 )((2x)/((1+x^2 )^2 )) ⇒(1+x^2 )^2 y′′=−C_1 sin (tan^(−1) x+C_2 )−2xC_1 cos (tan^(−1) x+C_2 ) ⇒(1+x^2 )^2 y′′=−y−2x(1+x^2 )y′ ⇒(1+x^2 )^2 y′′+2x(1+x^2 )y′+y=0 ✓

$${check}: \\ $$$${y}'={C}_{\mathrm{1}} \mathrm{cos}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right)×\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}'=\mathrm{2}{xC}_{\mathrm{1}} \mathrm{cos}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right) \\ $$$${y}''=−{C}_{\mathrm{1}} \mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right)×\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }−{C}_{\mathrm{1}} \:\mathrm{cos}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right)\frac{\mathrm{2}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} {y}''=−{C}_{\mathrm{1}} \mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right)−\mathrm{2}{xC}_{\mathrm{1}} \:\mathrm{cos}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right) \\ $$$$\Rightarrow\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} {y}''=−{y}−\mathrm{2}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}' \\ $$$$\Rightarrow\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} {y}''+\mathrm{2}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}'+{y}=\mathrm{0}\:\checkmark \\ $$

Answered by MathematicalUser2357 last updated on 21/Apr/25

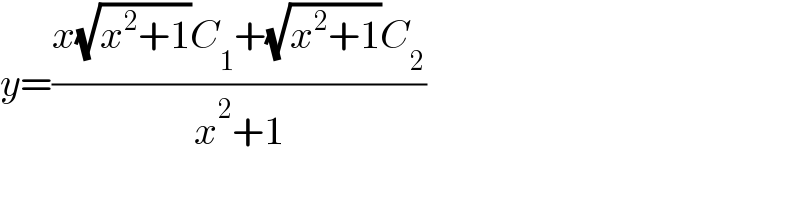
y=((x(√(x^2 +1))C_1 +(√(x^2 +1))C_2 )/(x^2 +1))

$${y}=\frac{{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{C}_{\mathrm{1}} +\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{C}_{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$

Commented by mnjuly1970 last updated on 21/Apr/25

thx please solution with details

$$\:{thx}\:\:{please}\:{solution}\:{with}\:{details} \\ $$

Commented by MathematicalUser2357 last updated on 22/Apr/25

solution with details (so, I can′t solve by hand, so WolframAlpha solved for me!)

$$\mathrm{solution}\:\mathrm{with}\:\mathrm{details} \\ $$$$\left(\mathrm{so},\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{hand},\:\mathrm{so}\:\mathrm{WolframAlpha}\:\mathrm{solved}\:\mathrm{for}\:\mathrm{me}!\right) \\ $$

Answered by Ghisom last updated on 21/Apr/25

this one is somehow obvious [at least with some experience] multiply the equation with (1+x^2 )^(1/2) (1+x^2 )^(5/2) y′′+2x(1+x^2 )^(3/2) y′+(1+x^2 )^(1/2) y=0 assume y=((ax+b)/( (1+x^2 )^(1/2) )) ⇒ y′=−((bx−a)/((1+x^2 )^(3/2) )) ⇒ y′′=((2bx^2 −3ax−b)/((1+x^2 )^(5/2) )) inserting above ⇒ true

$$\mathrm{this}\:\mathrm{one}\:\mathrm{is}\:\mathrm{somehow}\:\mathrm{obvious}\:\left[\mathrm{at}\:\mathrm{least}\:\mathrm{with}\right. \\ $$$$\left.\mathrm{some}\:\mathrm{experience}\right] \\ $$$$\mathrm{multiply}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{with}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} {y}''+\mathrm{2}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} {y}'+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} {y}=\mathrm{0} \\ $$$$\mathrm{assume}\:{y}=\frac{{ax}+{b}}{\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} } \\ $$$$\Rightarrow\:{y}'=−\frac{{bx}−{a}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\Rightarrow\:{y}''=\frac{\mathrm{2}{bx}^{\mathrm{2}} −\mathrm{3}{ax}−{b}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} } \\ $$$$\mathrm{inserting}\:\mathrm{above}\:\Rightarrow\:\mathrm{true} \\ $$

Answered by mr W last updated on 22/Apr/25

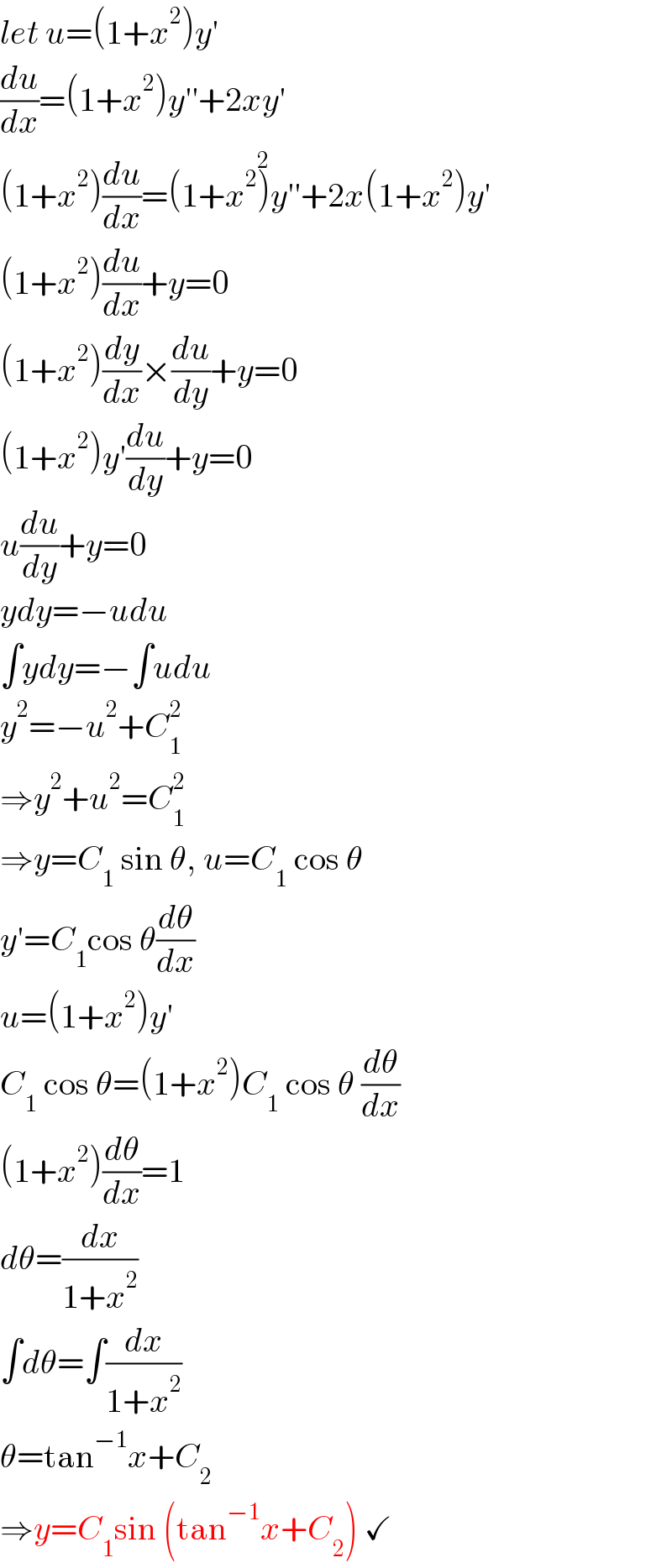
let u=(1+x^2 )y′ (du/dx)=(1+x^2 )y′′+2xy′ (1+x^2 )(du/dx)=(1+x^2 )^2 y′′+2x(1+x^2 )y′ (1+x^2 )(du/dx)+y=0 (1+x^2 )(dy/dx)×(du/dy)+y=0 (1+x^2 )y′(du/dy)+y=0 u(du/dy)+y=0 ydy=−udu ∫ydy=−∫udu y^2 =−u^2 +C_1 ^2 ⇒y^2 +u^2 =C_1 ^2 ⇒y=C_1 sin θ, u=C_1 cos θ y′=C_1 cos θ(dθ/dx) u=(1+x^2 )y′ C_1 cos θ=(1+x^2 )C_1 cos θ (dθ/dx) (1+x^2 )(dθ/dx)=1 dθ=(dx/(1+x^2 )) ∫dθ=∫(dx/(1+x^2 )) θ=tan^(−1) x+C_2 ⇒y=C_1 sin (tan^(−1) x+C_2 ) ✓

$${let}\:{u}=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}' \\ $$$$\frac{{du}}{{dx}}=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}''+\mathrm{2}{xy}' \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\frac{{du}}{{dx}}=\left(\mathrm{1}+{x}^{\mathrm{2}} \overset{\mathrm{2}} {\right)}{y}''+\mathrm{2}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}' \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\frac{{du}}{{dx}}+{y}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}×\frac{{du}}{{dy}}+{y}=\mathrm{0} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}'\frac{{du}}{{dy}}+{y}=\mathrm{0} \\ $$$${u}\frac{{du}}{{dy}}+{y}=\mathrm{0} \\ $$$${ydy}=−{udu} \\ $$$$\int{ydy}=−\int{udu} \\ $$$${y}^{\mathrm{2}} =−{u}^{\mathrm{2}} +{C}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow{y}^{\mathrm{2}} +{u}^{\mathrm{2}} ={C}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow{y}={C}_{\mathrm{1}} \:\mathrm{sin}\:\theta,\:{u}={C}_{\mathrm{1}} \:\mathrm{cos}\:\theta \\ $$$${y}'={C}_{\mathrm{1}} \mathrm{cos}\:\theta\frac{{d}\theta}{{dx}} \\ $$$${u}=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}' \\ $$$${C}_{\mathrm{1}} \:\mathrm{cos}\:\theta=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){C}_{\mathrm{1}} \:\mathrm{cos}\:\theta\:\frac{{d}\theta}{{dx}} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\frac{{d}\theta}{{dx}}=\mathrm{1} \\ $$$${d}\theta=\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\int{d}\theta=\int\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\theta=\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$$\Rightarrow{y}={C}_{\mathrm{1}} \mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right)\:\checkmark \\ $$

Commented by mr W last updated on 23/Apr/25

tan^(−1) x=sin^(−1) (x/( (√(1+x^2 ))))=cos^(−1) (1/( (√(1+x^2 )))) y=C_1 sin (tan^(−1) x+C_2 ) =C_1 [sin (tan^(−1) x) cos C_2 +cos (tan^(−1) x) sin C_2 ] =C_1 [sin (sin^(−1) (x/( (√(1+x^2 ))))) cos C_2 +cos (cos^(−1) (1/( (√(1+x^2 ))))) sin C_2 ] =C_1 [(x/( (√(1+x^2 )))) cos C_2 +(1/( (√(1+x^2 )))) sin C_2 ] =((c_1 x+c_2 )/( (√(1+x^2 )))) that means the result can also be expressed as y=((C_1 x+C_2 )/( (√(1+x^2 )))).

$$\mathrm{tan}^{−\mathrm{1}} {x}=\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${y}={C}_{\mathrm{1}} \mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}+{C}_{\mathrm{2}} \right) \\ $$$$\:\:\:={C}_{\mathrm{1}} \left[\mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}\right)\:\mathrm{cos}\:{C}_{\mathrm{2}} +\mathrm{cos}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}\right)\:\mathrm{sin}\:{C}_{\mathrm{2}} \right] \\ $$$$\:\:\:={C}_{\mathrm{1}} \left[\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)\:\mathrm{cos}\:{C}_{\mathrm{2}} +\mathrm{cos}\:\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)\:\mathrm{sin}\:{C}_{\mathrm{2}} \right] \\ $$$$\:\:\:={C}_{\mathrm{1}} \left[\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\mathrm{cos}\:{C}_{\mathrm{2}} +\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\mathrm{sin}\:{C}_{\mathrm{2}} \right] \\ $$$$\:\:\:=\frac{{c}_{\mathrm{1}} {x}+{c}_{\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${that}\:{means}\:{the}\:{result}\:{can}\:{also} \\ $$$${be}\:{expressed}\:{as}\:{y}=\frac{{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}. \\ $$

Commented by Ghisom last updated on 23/Apr/25

nice!

$$\mathrm{nice}! \\ $$

Commented by mnjuly1970 last updated on 23/Apr/25

thanks alot sir W

$${thanks}\:{alot}\:{sir}\:{W} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com