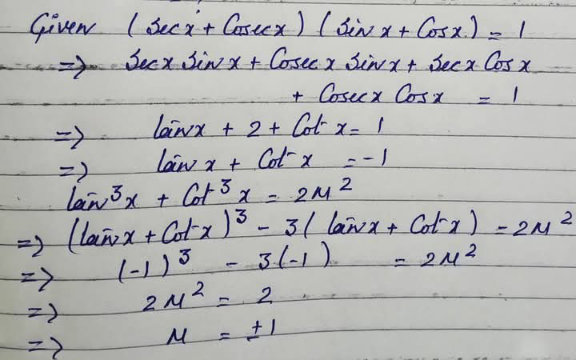Question Number 218889 by Spillover last updated on 17/Apr/25

Answered by mehdee7396 last updated on 17/Apr/25
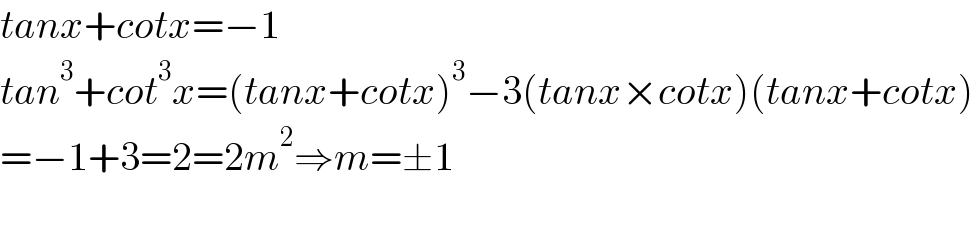
$${tanx}+{cotx}=−\mathrm{1} \\ $$$${tan}^{\mathrm{3}} +{cot}^{\mathrm{3}} {x}=\left({tanx}+{cotx}\right)^{\mathrm{3}} −\mathrm{3}\left({tanx}×{cotx}\right)\left({tanx}+{cotx}\right) \\ $$$$=−\mathrm{1}+\mathrm{3}=\mathrm{2}=\mathrm{2}{m}^{\mathrm{2}} \Rightarrow{m}=\pm\mathrm{1} \\ $$$$ \\ $$
Answered by som(math1967) last updated on 17/Apr/25
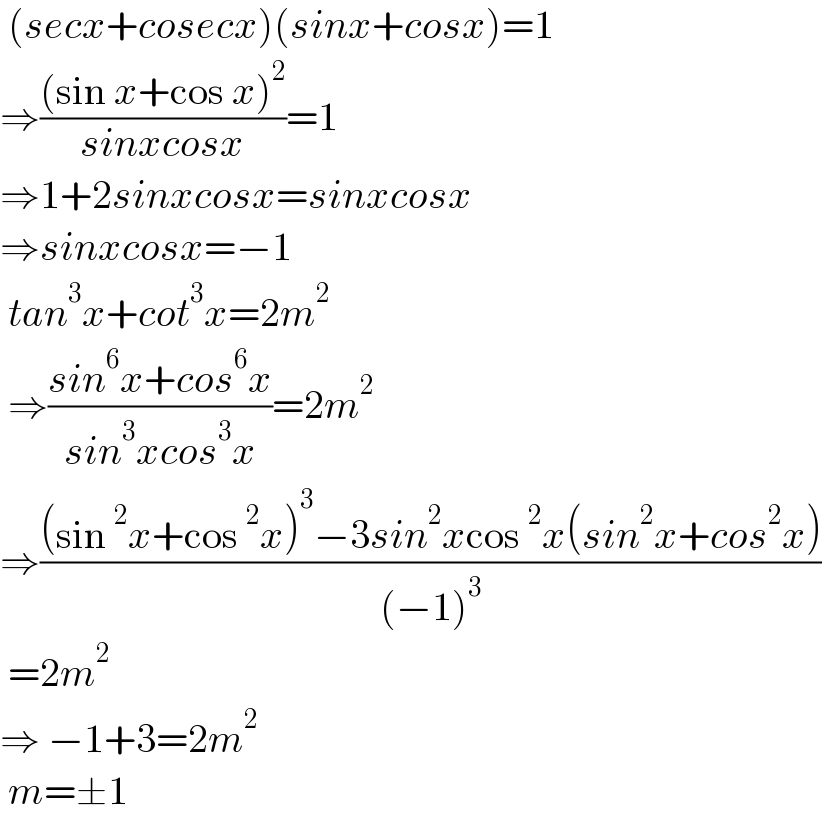
$$\:\left({secx}+{cosecx}\right)\left({sinx}+{cosx}\right)=\mathrm{1} \\ $$$$\Rightarrow\frac{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }{{sinxcosx}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2}{sinxcosx}={sinxcosx} \\ $$$$\Rightarrow{sinxcosx}=−\mathrm{1} \\ $$$$\:{tan}^{\mathrm{3}} {x}+{cot}^{\mathrm{3}} {x}=\mathrm{2}{m}^{\mathrm{2}} \\ $$$$\:\Rightarrow\frac{{sin}^{\mathrm{6}} {x}+{cos}^{\mathrm{6}} {x}}{{sin}^{\mathrm{3}} {xcos}^{\mathrm{3}} {x}}=\mathrm{2}{m}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\left(\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\mathrm{3}{sin}^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}\left({sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}\right)}{\left(−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\:=\mathrm{2}{m}^{\mathrm{2}} \\ $$$$\Rightarrow\:−\mathrm{1}+\mathrm{3}=\mathrm{2}{m}^{\mathrm{2}} \\ $$$$\:{m}=\pm\mathrm{1} \\ $$
Answered by Spillover last updated on 17/Apr/25

Answered by Spillover last updated on 17/Apr/25
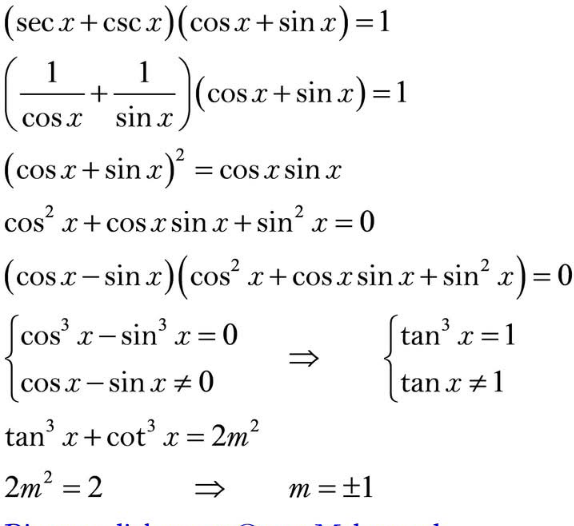
Answered by Spillover last updated on 17/Apr/25