Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 218850 by hardmath last updated on 16/Apr/25

Answered by MrGaster last updated on 17/Apr/25

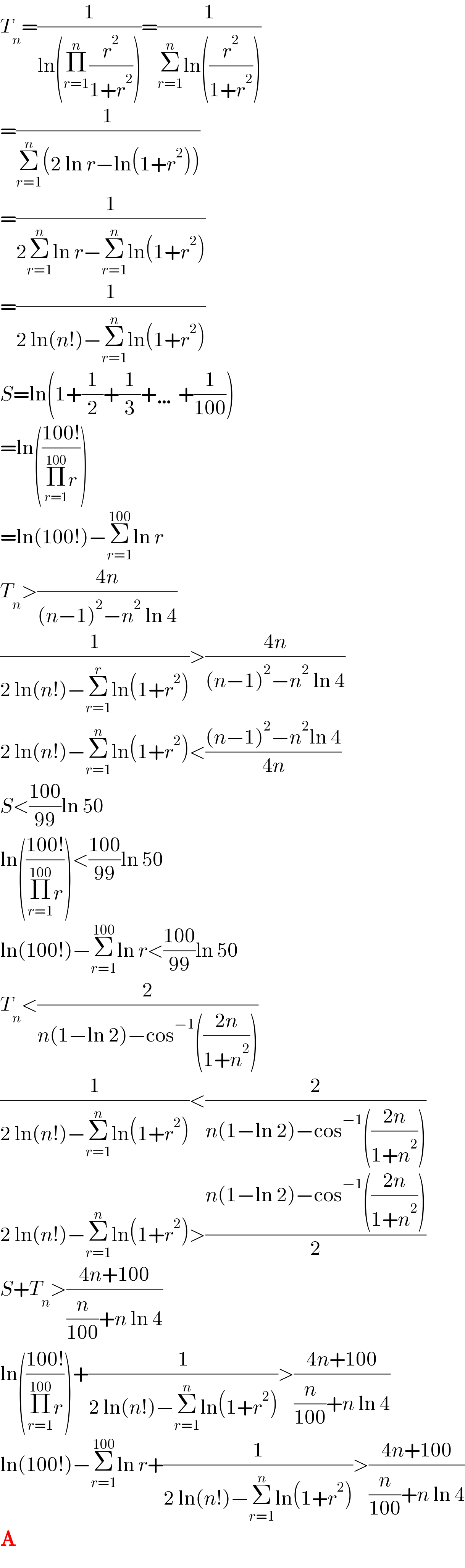
T_n =(1/(ln(Π_(r=1) ^n (r^2 /(1+r^2 )))))=(1/(Σ_(r=1) ^n ln((r^2 /(1+r^2 ))))) =(1/(Σ_(r=1) ^n (2 ln r−ln(1+r^2 )))) =(1/(2Σ_(r=1) ^n ln r−Σ_(r=1) ^n ln(1+r^2 ))) =(1/(2 ln(n!)−Σ_(r=1) ^n ln(1+r^2 ))) S=ln(1+(1/2)+(1/3)+…+(1/(100))) =ln(((100!)/(Π_(r=1) ^(100) r))) =ln(100!)−Σ_(r=1) ^(100) ln r T_n >((4n)/((n−1)^2 −n^2 ln 4)) (1/(2 ln(n!)−Σ_(r=1) ^r ln(1+r^2 )))>((4n)/((n−1)^2 −n^2 ln 4)) 2 ln(n!)−Σ_(r=1) ^n ln(1+r^2 )<(((n−1)^2 −n^2 ln 4)/(4n)) S<((100)/(99))ln 50 ln(((100!)/(Π_(r=1) ^(100) r)))<((100)/(99))ln 50 ln(100!)−Σ_(r=1) ^(100) ln r<((100)/(99))ln 50 T_n <(2/(n(1−ln 2)−cos^(−1) (((2n)/(1+n^2 ))))) (1/(2 ln(n!)−Σ_(r=1) ^n ln(1+r^2 )))<(2/(n(1−ln 2)−cos^(−1) (((2n)/(1+n^2 ))))) 2 ln(n!)−Σ_(r=1) ^n ln(1+r^2 )>((n(1−ln 2)−cos^(−1) (((2n)/(1+n^2 ))))/2) S+T_n >((4n+100)/((n/(100))+n ln 4)) ln(((100!)/(Π_(r=1) ^(100) r)))+(1/(2 ln(n!)−Σ_(r=1) ^n ln(1+r^2 )))>((4n+100)/((n/(100))+n ln 4)) ln(100!)−Σ_(r=1) ^(100) ln r+(1/(2 ln(n!)−Σ_(r=1) ^n ln(1+r^2 )))>((4n+100)/((n/(100))+n ln 4)) A

$${T}_{{n}} =\frac{\mathrm{1}}{\mathrm{ln}\left(\underset{{r}=\mathrm{1}} {\overset{{n}} {\prod}}\frac{{r}^{\mathrm{2}} }{\mathrm{1}+{r}^{\mathrm{2}} }\right)}=\frac{\mathrm{1}}{\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\frac{{r}^{\mathrm{2}} }{\mathrm{1}+{r}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\mathrm{1}}{\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{2}\:\mathrm{ln}\:{r}−\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\:{r}−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{ln}\left({n}!\right)−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)} \\ $$$${S}=\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\ldots+\frac{\mathrm{1}}{\mathrm{100}}\right) \\ $$$$=\mathrm{ln}\left(\frac{\mathrm{100}!}{\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\prod}}{r}}\right) \\ $$$$=\mathrm{ln}\left(\mathrm{100}!\right)−\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\mathrm{ln}\:{r} \\ $$$${T}_{{n}} >\frac{\mathrm{4}{n}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} −{n}^{\mathrm{2}} \:\mathrm{ln}\:\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{ln}\left({n}!\right)−\underset{{r}=\mathrm{1}} {\overset{{r}} {\sum}}\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)}>\frac{\mathrm{4}{n}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} −{n}^{\mathrm{2}} \:\mathrm{ln}\:\mathrm{4}} \\ $$$$\mathrm{2}\:\mathrm{ln}\left({n}!\right)−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)<\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} −{n}^{\mathrm{2}} \mathrm{ln}\:\mathrm{4}}{\mathrm{4}{n}} \\ $$$${S}<\frac{\mathrm{100}}{\mathrm{99}}\mathrm{ln}\:\mathrm{50} \\ $$$$\mathrm{ln}\left(\frac{\mathrm{100}!}{\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\prod}}{r}}\right)<\frac{\mathrm{100}}{\mathrm{99}}\mathrm{ln}\:\mathrm{50} \\ $$$$\mathrm{ln}\left(\mathrm{100}!\right)−\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\mathrm{ln}\:{r}<\frac{\mathrm{100}}{\mathrm{99}}\mathrm{ln}\:\mathrm{50} \\ $$$${T}_{{n}} <\frac{\mathrm{2}}{{n}\left(\mathrm{1}−\mathrm{ln}\:\mathrm{2}\right)−\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}{n}}{\mathrm{1}+{n}^{\mathrm{2}} }\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{ln}\left({n}!\right)−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)}<\frac{\mathrm{2}}{{n}\left(\mathrm{1}−\mathrm{ln}\:\mathrm{2}\right)−\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}{n}}{\mathrm{1}+{n}^{\mathrm{2}} }\right)} \\ $$$$\mathrm{2}\:\mathrm{ln}\left({n}!\right)−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)>\frac{{n}\left(\mathrm{1}−\mathrm{ln}\:\mathrm{2}\right)−\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}{n}}{\mathrm{1}+{n}^{\mathrm{2}} }\right)}{\mathrm{2}} \\ $$$${S}+{T}_{{n}} >\frac{\mathrm{4}{n}+\mathrm{100}}{\frac{{n}}{\mathrm{100}}+{n}\:\mathrm{ln}\:\mathrm{4}} \\ $$$$\mathrm{ln}\left(\frac{\mathrm{100}!}{\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\prod}}{r}}\right)+\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{ln}\left({n}!\right)−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)}>\frac{\mathrm{4}{n}+\mathrm{100}}{\frac{{n}}{\mathrm{100}}+{n}\:\mathrm{ln}\:\mathrm{4}} \\ $$$$\mathrm{ln}\left(\mathrm{100}!\right)−\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\mathrm{ln}\:{r}+\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{ln}\left({n}!\right)−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+{r}^{\mathrm{2}} \right)}>\frac{\mathrm{4}{n}+\mathrm{100}}{\frac{{n}}{\mathrm{100}}+{n}\:\mathrm{ln}\:\mathrm{4}} \\ $$$$\boldsymbol{\mathrm{A}} \\ $$

Commented by hardmath last updated on 17/Apr/25

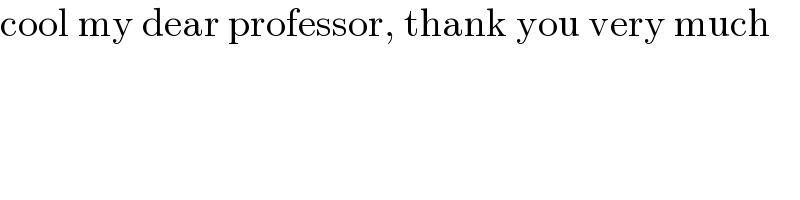
cool my dear professor, thank you very much

$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{professor},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com