
Question Number 218833 by Spillover last updated on 16/Apr/25
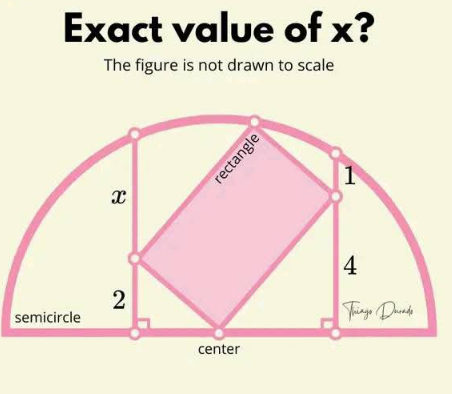
Answered by mr W last updated on 16/Apr/25
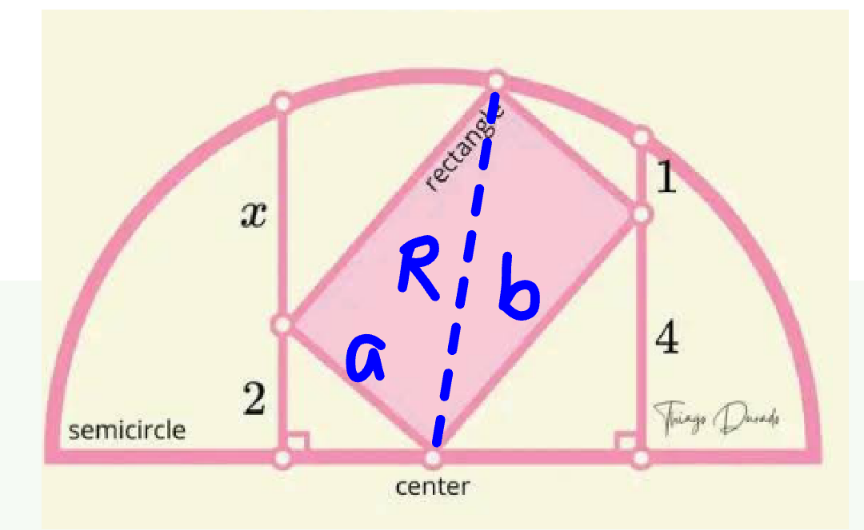
Commented by mr W last updated on 16/Apr/25
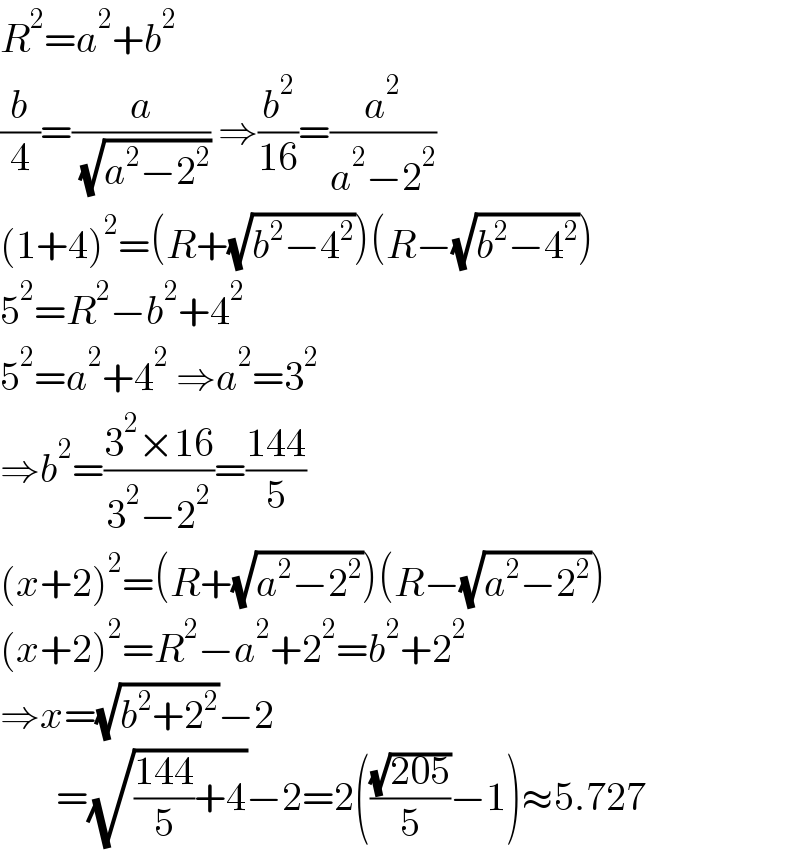
$${R}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\frac{{b}}{\mathrm{4}}=\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }}\:\Rightarrow\frac{{b}^{\mathrm{2}} }{\mathrm{16}}=\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}+\mathrm{4}\right)^{\mathrm{2}} =\left({R}+\sqrt{{b}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }\right)\left({R}−\sqrt{{b}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }\right) \\ $$$$\mathrm{5}^{\mathrm{2}} ={R}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} \\ $$$$\mathrm{5}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} \:\Rightarrow{a}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} =\frac{\mathrm{3}^{\mathrm{2}} ×\mathrm{16}}{\mathrm{3}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{144}}{\mathrm{5}} \\ $$$$\left({x}+\mathrm{2}\right)^{\mathrm{2}} =\left({R}+\sqrt{{a}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\right)\left({R}−\sqrt{{a}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\right) \\ $$$$\left({x}+\mathrm{2}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} −{a}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} ={b}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\sqrt{{b}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:=\sqrt{\frac{\mathrm{144}}{\mathrm{5}}+\mathrm{4}}−\mathrm{2}=\mathrm{2}\left(\frac{\sqrt{\mathrm{205}}}{\mathrm{5}}−\mathrm{1}\right)\approx\mathrm{5}.\mathrm{727} \\ $$
Commented by Spillover last updated on 16/Apr/25
$${great}\:{work}.{thanks} \\ $$
Answered by Spillover last updated on 16/Apr/25
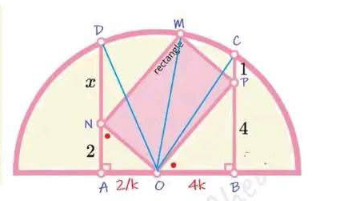
Answered by Spillover last updated on 16/Apr/25

