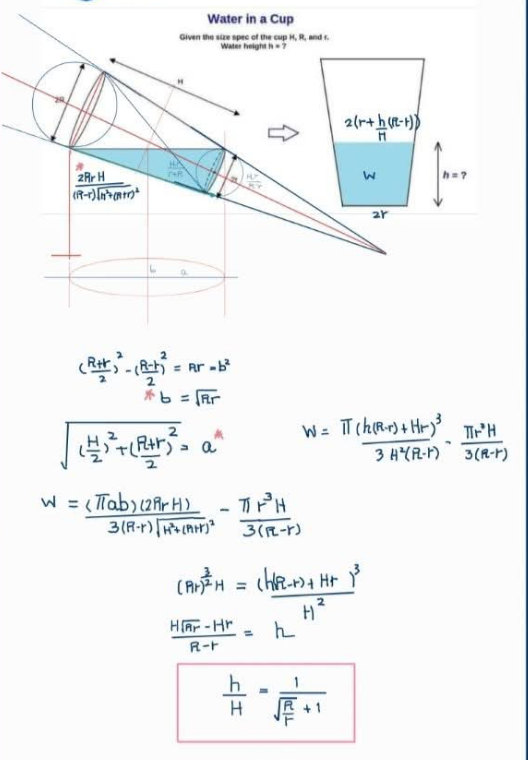
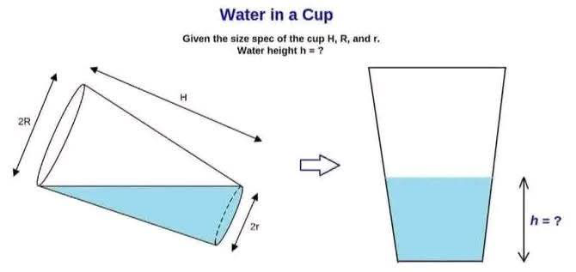
Question Number 218778 by Spillover last updated on 15/Apr/25
Answered by mr W last updated on 15/Apr/25
Commented by mr W last updated on 17/Apr/25
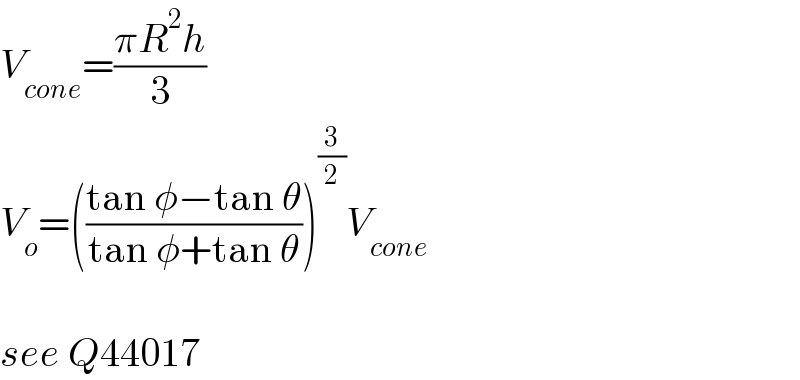
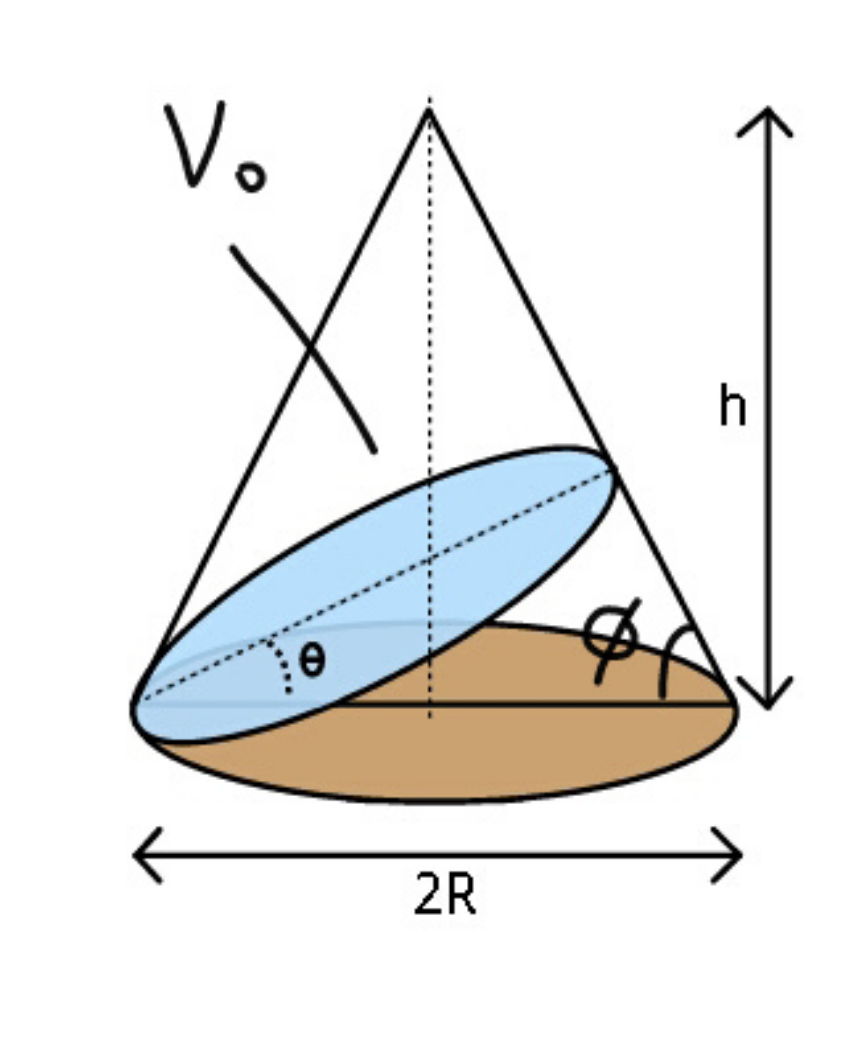
$${V}_{{cone}} =\frac{\pi{R}^{\mathrm{2}} {h}}{\mathrm{3}} \\ $$$${V}_{{o}} =\left(\frac{\mathrm{tan}\:\phi−\mathrm{tan}\:\theta}{\mathrm{tan}\:\phi+\mathrm{tan}\:\theta}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {V}_{{cone}} \\ $$$$ \\ $$$${see}\:{Q}\mathrm{44017} \\ $$
Commented by mr W last updated on 15/Apr/25
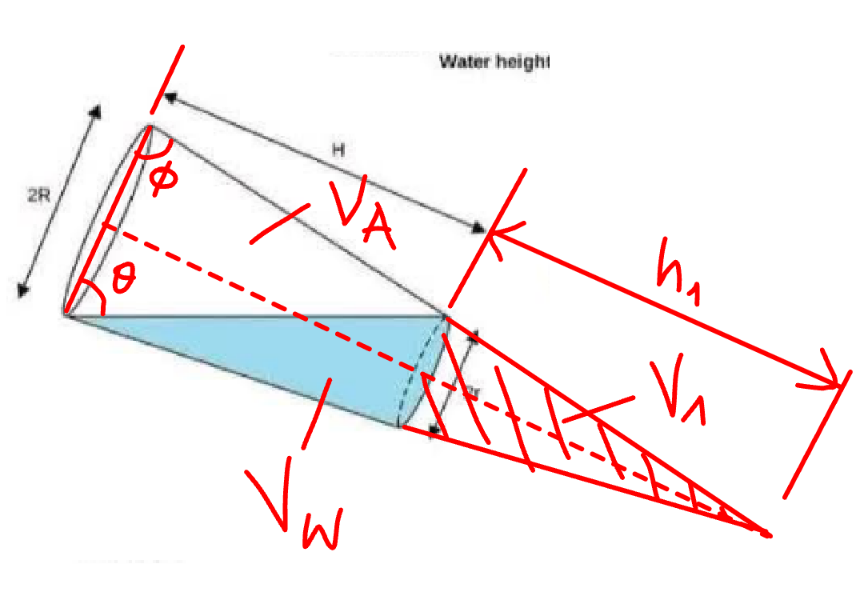
Commented by mr W last updated on 15/Apr/25
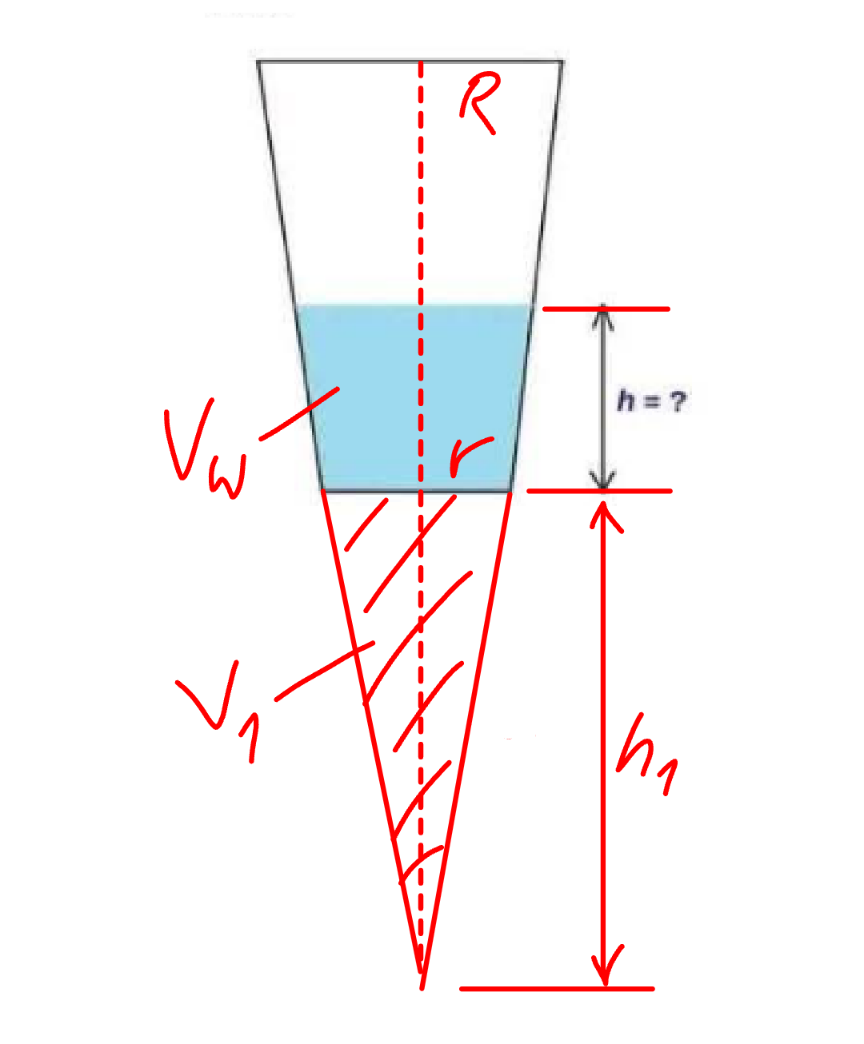
Commented by mr W last updated on 18/Apr/25
![((h_1 +H)/h_1 )=(R/r) ⇒h_1 =(H/((R/r)−1)) tan φ=(H/(R−r)) tan θ=(H/(R+r)) ((tan φ−tan θ)/(tan φ+tan θ))=(((H/(R−r))−(H/(R+r)))/((H/(R−r))+(H/(R+r))))=(r/R) V_1 =((πr^2 h_1 )/3)=((πr^3 H)/(3(R−r))) V_(Total) =((R/r))^3 V_1 V_W +V_1 =(((tan φ−tan θ)/(tan φ+tan θ)))^(3/2) V_(Total) V_W +V_1 =((r/R))^(3/2) ((R/r))^3 V_1 =((R/r))^(3/2) V_1 V_W =[((R/r))^(3/2) −1]V_1 V_W =((πr^3 H)/(3(R−r)))[((R/r))^(3/2) −1] V_W +V_1 =(((h+h_1 )/h_1 ))^3 V_1 V_W =[((h/h_1 )+1)^3 −1]V_1 [((R/r))^(3/2) −1]V_1 =[((h/h_1 )+1)^3 −1]V_1 ((R/r))^(3/2) =((h/h_1 )+1)^3 (h/h_1 )=(√(R/r))−1 ⇒h=(H/((R/r)−1))((√(R/r))−1)=(H/( (√(R/r))+1)) ✓](Q218796.png)
$$\frac{{h}_{\mathrm{1}} +{H}}{{h}_{\mathrm{1}} }=\frac{{R}}{{r}}\:\Rightarrow{h}_{\mathrm{1}} =\frac{{H}}{\frac{{R}}{{r}}−\mathrm{1}} \\ $$$$\mathrm{tan}\:\phi=\frac{{H}}{{R}−{r}} \\ $$$$\mathrm{tan}\:\theta=\frac{{H}}{{R}+{r}} \\ $$$$\frac{\mathrm{tan}\:\phi−\mathrm{tan}\:\theta}{\mathrm{tan}\:\phi+\mathrm{tan}\:\theta}=\frac{\frac{{H}}{{R}−{r}}−\frac{{H}}{{R}+{r}}}{\frac{{H}}{{R}−{r}}+\frac{{H}}{{R}+{r}}}=\frac{{r}}{{R}} \\ $$$${V}_{\mathrm{1}} =\frac{\pi{r}^{\mathrm{2}} {h}_{\mathrm{1}} }{\mathrm{3}}=\frac{\pi{r}^{\mathrm{3}} {H}}{\mathrm{3}\left({R}−{r}\right)} \\ $$$${V}_{{Total}} =\left(\frac{{R}}{{r}}\right)^{\mathrm{3}} {V}_{\mathrm{1}} \\ $$$${V}_{{W}} +{V}_{\mathrm{1}} =\left(\frac{\mathrm{tan}\:\phi−\mathrm{tan}\:\theta}{\mathrm{tan}\:\phi+\mathrm{tan}\:\theta}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {V}_{{Total}} \\ $$$${V}_{{W}} +{V}_{\mathrm{1}} =\left(\frac{{r}}{{R}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\frac{{R}}{{r}}\right)^{\mathrm{3}} {V}_{\mathrm{1}} =\left(\frac{{R}}{{r}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {V}_{\mathrm{1}} \\ $$$${V}_{{W}} =\left[\left(\frac{{R}}{{r}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{1}\right]{V}_{\mathrm{1}} \\ $$$${V}_{{W}} =\frac{\pi{r}^{\mathrm{3}} {H}}{\mathrm{3}\left({R}−{r}\right)}\left[\left(\frac{{R}}{{r}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{1}\right] \\ $$$$ \\ $$$${V}_{{W}} +{V}_{\mathrm{1}} =\left(\frac{{h}+{h}_{\mathrm{1}} }{{h}_{\mathrm{1}} }\right)^{\mathrm{3}} {V}_{\mathrm{1}} \\ $$$${V}_{{W}} =\left[\left(\frac{{h}}{{h}_{\mathrm{1}} }+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{1}\right]{V}_{\mathrm{1}} \\ $$$$\left[\left(\frac{{R}}{{r}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{1}\right]{V}_{\mathrm{1}} =\left[\left(\frac{{h}}{{h}_{\mathrm{1}} }+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{1}\right]{V}_{\mathrm{1}} \\ $$$$\left(\frac{{R}}{{r}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\left(\frac{{h}}{{h}_{\mathrm{1}} }+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\frac{{h}}{{h}_{\mathrm{1}} }=\sqrt{\frac{{R}}{{r}}}−\mathrm{1} \\ $$$$\Rightarrow{h}=\frac{{H}}{\frac{{R}}{{r}}−\mathrm{1}}\left(\sqrt{\frac{{R}}{{r}}}−\mathrm{1}\right)=\frac{{H}}{\:\sqrt{\frac{{R}}{{r}}}+\mathrm{1}}\:\checkmark \\ $$
Commented by Spillover last updated on 15/Apr/25
$${Wonderfull}\:{solution}.{thank}\:{you} \\ $$
Answered by Spillover last updated on 15/Apr/25
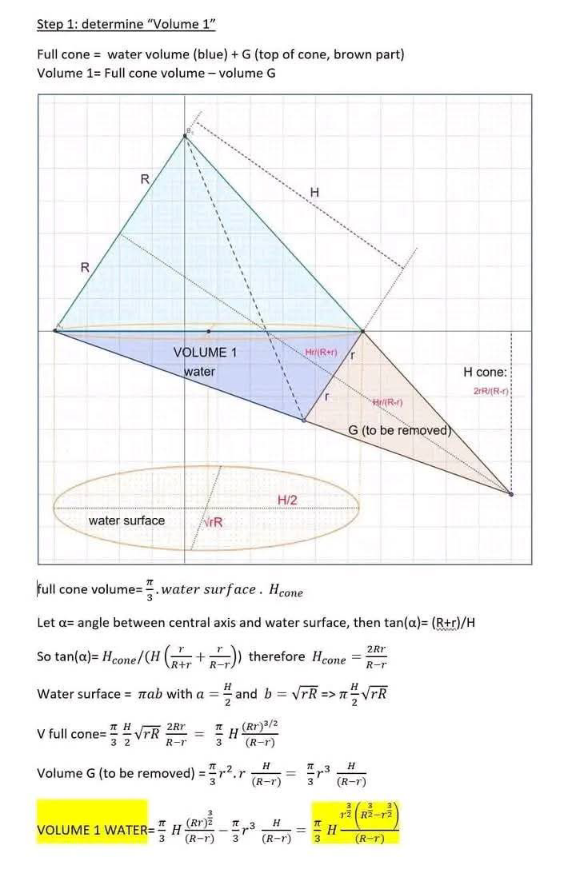
Answered by Spillover last updated on 15/Apr/25
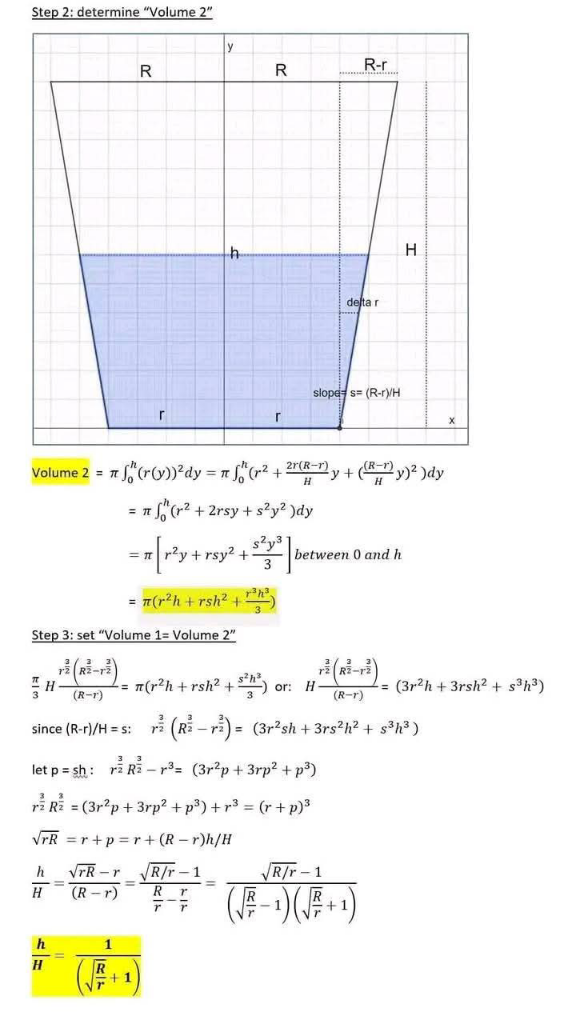
Answered by Spillover last updated on 17/Apr/25