
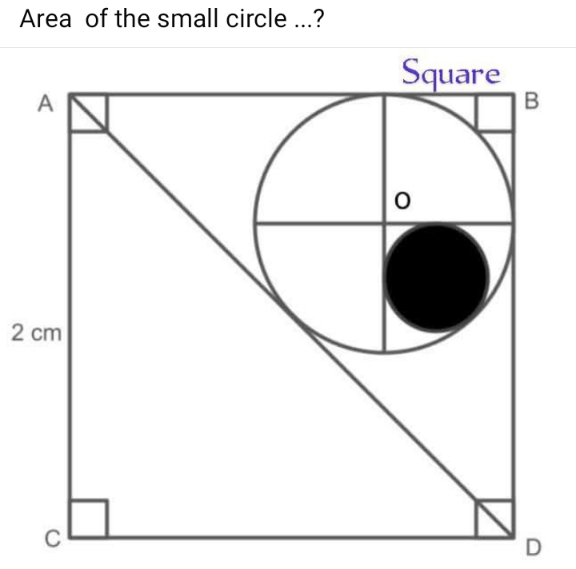
Question Number 218735 by Spillover last updated on 14/Apr/25
Answered by som(math1967) last updated on 15/Apr/25
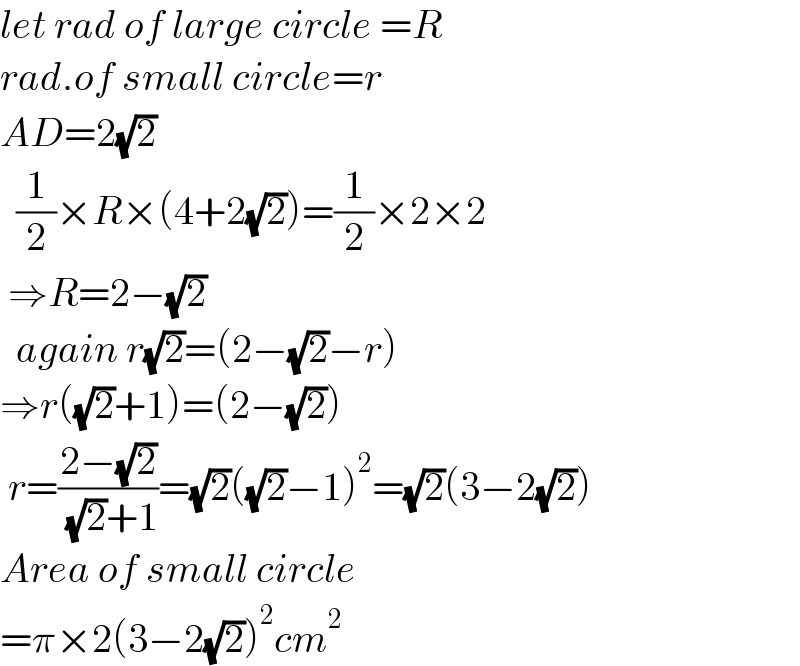
$${let}\:{rad}\:{of}\:{large}\:{circle}\:={R} \\ $$$${rad}.{of}\:{small}\:{circle}={r} \\ $$$${AD}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{2}}×{R}×\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×\mathrm{2} \\ $$$$\:\Rightarrow{R}=\mathrm{2}−\sqrt{\mathrm{2}} \\ $$$$\:\:{again}\:{r}\sqrt{\mathrm{2}}=\left(\mathrm{2}−\sqrt{\mathrm{2}}−{r}\right) \\ $$$$\Rightarrow{r}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)=\left(\mathrm{2}−\sqrt{\mathrm{2}}\right) \\ $$$$\:{r}=\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}=\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} =\sqrt{\mathrm{2}}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$$${Area}\:{of}\:{small}\:{circle} \\ $$$$=\pi×\mathrm{2}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} {cm}^{\mathrm{2}} \\ $$
Commented by Spillover last updated on 16/Apr/25
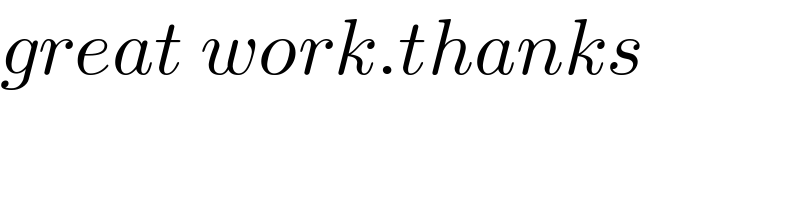
$${great}\:{work}.{thanks}\: \\ $$
Answered by A5T last updated on 15/Apr/25
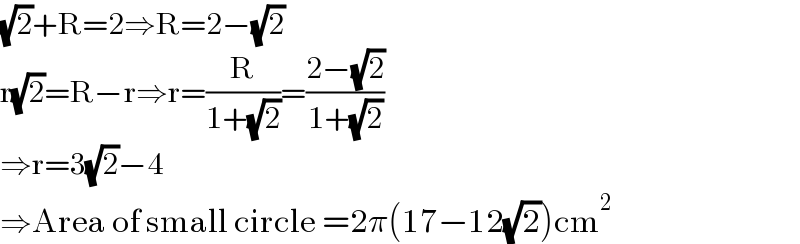
$$\sqrt{\mathrm{2}}+\mathrm{R}=\mathrm{2}\Rightarrow\mathrm{R}=\mathrm{2}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{r}\sqrt{\mathrm{2}}=\mathrm{R}−\mathrm{r}\Rightarrow\mathrm{r}=\frac{\mathrm{R}}{\mathrm{1}+\sqrt{\mathrm{2}}}=\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{r}=\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{4} \\ $$$$\Rightarrow\mathrm{Area}\:\mathrm{of}\:\mathrm{small}\:\mathrm{circle}\:=\mathrm{2}\pi\left(\mathrm{17}−\mathrm{12}\sqrt{\mathrm{2}}\right)\mathrm{cm}^{\mathrm{2}} \\ $$
Commented by Spillover last updated on 16/Apr/25
$${great}\:{work}.{thanks}\: \\ $$
Answered by Spillover last updated on 16/Apr/25

Answered by Spillover last updated on 16/Apr/25
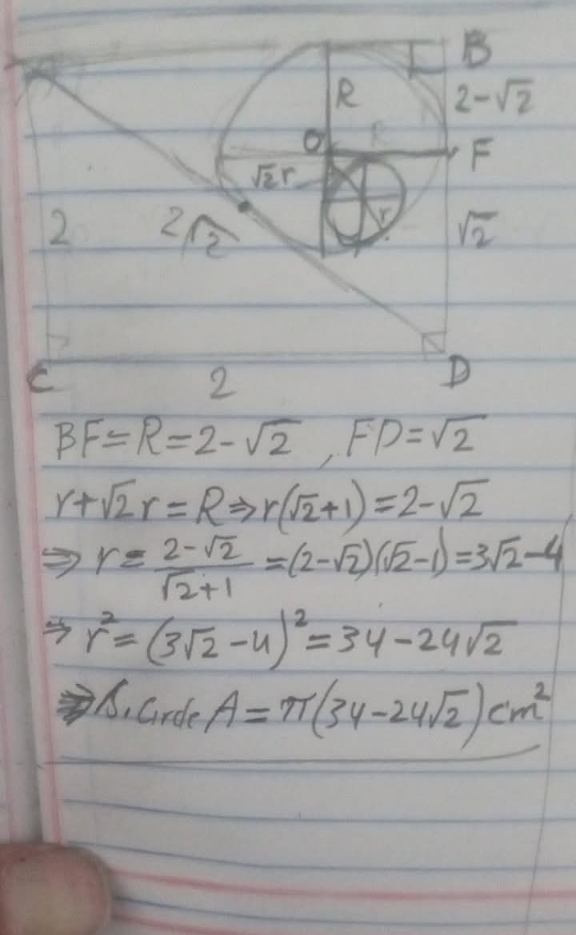
Answered by Spillover last updated on 16/Apr/25

