Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 218673 by Spillover last updated on 14/Apr/25

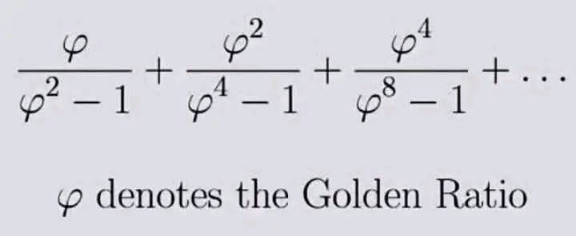
Commented by Nicholas666 last updated on 14/Apr/25

ϕ

$$\varphi \\ $$

Answered by Nicholas666 last updated on 14/Apr/25

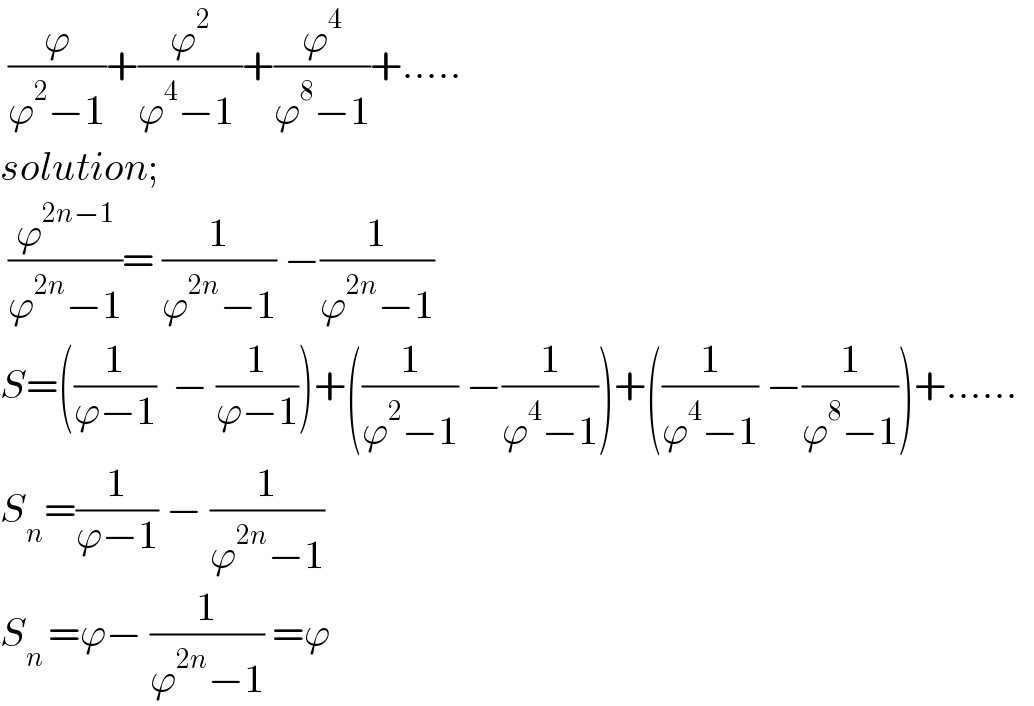
(ϕ/(ϕ^2 −1))+(ϕ^2 /(ϕ^4 −1 ))+(ϕ^4 /(ϕ^8 −1))+..... solution; (ϕ^(2n−1) /(ϕ^(2n) −1))= (1/(ϕ^(2n) −1)) −(1/(ϕ^(2n) −1)) S=((1/(ϕ−1)) − (1/(ϕ−1)))+((1/(ϕ^2 −1)) −(1/(ϕ^4 −1)))+((1/(ϕ^4 −1)) −(1/(ϕ^8 −1)))+...... S_n =(1/(ϕ−1)) − (1/(ϕ^(2n) −1)) S_(n ) =ϕ− (1/(ϕ^(2n) −1)) =ϕ

$$\:\frac{\varphi}{\varphi^{\mathrm{2}} −\mathrm{1}}+\frac{\varphi^{\mathrm{2}} }{\varphi^{\mathrm{4}} −\mathrm{1}\:}+\frac{\varphi^{\mathrm{4}} }{\varphi^{\mathrm{8}} −\mathrm{1}}+..... \\ $$$${solution}; \\ $$$$\:\frac{\varphi^{\mathrm{2}{n}−\mathrm{1}} }{\varphi^{\mathrm{2}{n}} −\mathrm{1}}=\:\frac{\mathrm{1}}{\varphi^{\mathrm{2}{n}} −\mathrm{1}}\:−\frac{\mathrm{1}}{\varphi^{\mathrm{2}{n}} −\mathrm{1}} \\ $$$${S}=\left(\frac{\mathrm{1}}{\varphi−\mathrm{1}}\:\:−\:\frac{\mathrm{1}}{\varphi−\mathrm{1}}\right)+\left(\frac{\mathrm{1}}{\varphi^{\mathrm{2}} −\mathrm{1}}\:−\frac{\mathrm{1}}{\varphi^{\mathrm{4}} −\mathrm{1}}\right)+\left(\frac{\mathrm{1}}{\varphi^{\mathrm{4}} −\mathrm{1}}\:−\frac{\mathrm{1}}{\varphi^{\mathrm{8}} −\mathrm{1}}\right)+......\:\: \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\varphi−\mathrm{1}}\:−\:\frac{\mathrm{1}}{\varphi^{\mathrm{2}{n}} −\mathrm{1}} \\ $$$${S}_{{n}\:} =\varphi−\:\frac{\mathrm{1}}{\varphi^{\mathrm{2}{n}} −\mathrm{1}}\:=\varphi\: \\ $$

Answered by Charleston last updated on 14/Apr/25

$$ \\ $$

Answered by Spillover last updated on 14/Apr/25

Terms of Service

Privacy Policy

Contact: info@tinkutara.com